高校入試の数学で必ず押さえておきたい一つが「内接円」。接点までの距離の性質や三平方の定理、円周角の定理など、重要な知識がギュッと詰まったテーマです。本記事では、過去問を通して解法パターンを整理し、効率よく理解できるようにまとめました。短時間で得点力アップを目指す受験生におすすめです。
近大和歌山 2025年度
問題
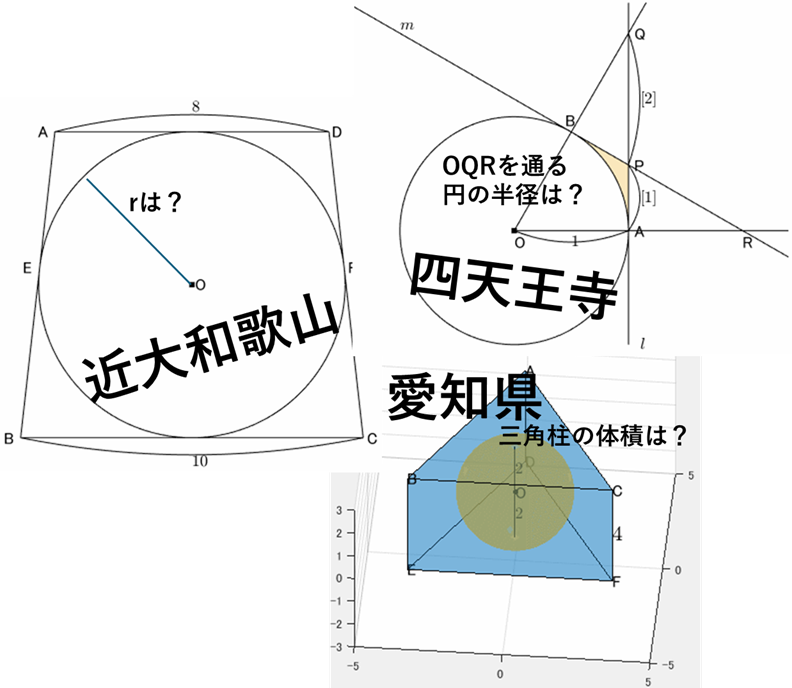
下図の等脚台形 $\mathrm{ABCD}$ について、
(1) 辺 $\mathrm{AB}$ の長さは?
(2) 内接円 $\mathrm{O}$ の半径は?

一気通貫アニメーション
このアニメーションが頭で自動再生されるまで何回も見てください。
解説
(1) 辺 $\mathrm{AB}$ の長さは?
等脚台形なので、左右は対象です。なので、$\mathrm{AD}$ は半分半分に分かれます。

そして、接点までの距離は等しいことより、

となります。同様に下側も考えて、

となりますので、$\mathrm{AB}=9$ です。
$$\mathrm{AB}=9$$
(2) 内接円 $\mathrm{O}$ の半径は?
内接円の半径 $r$ は、台形の高さの半分です。なので高さを求めましょう。
$\mathrm{AB}=9$ ということなので、ここを斜辺とする直角三角形を考えることにより、

が得られ、高さが分かりました。
$$\sqrt{80}=4\sqrt{5}$$
であり、この半分が内接円の半径 $r$ です。
$$r=2\sqrt{5}$$
四天王寺 2024年度
問題
円 $\mathrm{O}$ の半径は1。$\mathrm{AP}:\mathrm{PQ}=1:2$。

(1) 線分 $\mathrm{OQ}$ の長さは?
(2) 図の黄色部分の面積は?
(3) 3点 $\mathrm{O}$, $\mathrm{Q}$, $\mathrm{R}$ を通る円の半径は?
一気通貫アニメーション
(1)-(3)までを通しています。別々のものは個別の解説部分に載せます。
解説
(1) 線分 $\mathrm{OQ}$ の長さは?
一気通貫アニメーション
まずは (1) のみの一気通貫アニメーションです。
接点までの距離は等しい
接点までの距離は等しいので、$\mathrm{PA}=\mathrm{PB}$ です。

$\triangle\mathrm{PBQ}$ は直角三角形
直線 $m$ が接線であるので $\angle\mathrm{PBQ}=90^\circ$。
$\mathrm{PB}:\mathrm{PQ}=1:2$ より、$\triangle\mathrm{PBQ}$ は $60^\circ$, $90^\circ$, $30^\circ$ の直角三角形。

直線 $l$ も接線であるので $\angle\mathrm{OAQ}=90^\circ$。$\triangle\mathrm{OQA}=30^\circ$ なので、
$\triangle\mathrm{OAQ}$ は $60^\circ$, $90^\circ$, $30^\circ$ の直角三角形。
よって、$\mathrm{OQ}=2$。($\because\mathrm{OA}=1$)

$$\mathrm{OQ}=2$$
(2) 図の黄色部分の面積は?
方針を考える
扇形の面積はすぐに分かりますよね。なので、扇形と求める黄色部分を足した
四角形 $\mathrm{OAPB}$
の面積が分かればよい、ということになります。
そしてこの四角形 $\mathrm{OAPB}$ の面積は、直角三角形 $\mathrm{OAP}$ の面積の2倍です。
$\triangle\mathrm{OAP}$ の高さ $\mathrm{AP}$ は?
$\triangle\mathrm{OAP}$ の高さ $\mathrm{AP}$ は、$\mathrm{AQ}=\sqrt{3}$ が分かっているので既知です。

$\triangle\mathrm{OAP}$ の面積の2倍
四角形 $\mathrm{OAPB}$ の面積は $\triangle\mathrm{OAP}$ の面積の2倍であるので、
$$1\times\displaystyle\frac{\sqrt{3}}{3}$$

ここから扇形 $\mathrm{OAB}$ の面積である
$$\pi\cdot 1^2\times\frac{1}{6}$$
を引けばよいです。よって求める面積は、
$$\frac{\sqrt{3}}{3}-\frac{\pi}{6}$$
$$\frac{\sqrt{3}}{3}-\frac{\pi}{6}$$
(3) 3点 $\mathrm{O}$, $\mathrm{Q}$, $\mathrm{R}$ を通る円の半径は?
一気通貫アニメーション
円は3点が決まれば一意に決まる
円は3点が決まれば一意に決まります。なので、3点 $\mathrm{O}$, $\mathrm{Q}$, $\mathrm{R}$ を通る円は一意に書くことができて下記のようです。

ここまではなんとなく作図はできても、さて半径となるとどう求めてよいか悩みます。
何となく $\mathrm{P}$ は中心?と思う
少し勘を働かせて、
$\mathrm{P}$ が円の中心だったりして
なんて希望を持って眺めてみます。すると、$\angle\mathrm{QPR}$ は $120^\circ$ であることに気づきます。

これだけではまだ核心には迫れていませんが、$\mathrm{P}$ が円の中心であってほしいなぁ、と思いを込めれば、
$\angle\mathrm{O}=60^\circ$ であることに希望を持ち
実際にそうなっていることに気づきます。

根拠を明確にすることで $\mathrm{P}$ は中心であると確信する
円周角の定理より点 $\mathrm{P}$ は間違いなく円の中心であることが言えるので、
$\mathrm{PQ}=\displaystyle\frac{2\sqrt{3}}{3}$ が半径
です。アニメーションでは点 $\mathrm{P}$ が半径であることを強調するため、$\mathrm{PQ}$ を回転させて確認しています。
円の半径は、$\displaystyle\frac{2\sqrt{3}}{3}$
愛知県B 2018年度
問題
立体は正三角柱で、球 $\mathrm{O}$ は正三角柱にちょうど入っている。
球 $\mathrm{O}$ の半径が $2\mathrm{cm}$ のとき、正三角柱の体積は?

この問題は(2)。(1)は球の表面積を問うているが、ここでは省略。
一気通貫アニメーション
解説
高さは球の半径の倍
三角柱の体積を求めるので、底面積と高さが分かればよいです。高さはすぐに分かります。球の半径が $2$ ということより、高さはその倍の $4$ です。

底面積は真ん中で切った図形で考える
重心に気づけば高さは容易に分かる
あとは底面積である正三角形の面積を求めればよいことになります。
正三角柱にちょうど入っているということは、どの面も球に接しているということであり、柱の面は高さ半分のところで接しています。そこで、柱の半分のところで切ってみて平面で考えてみます。
立体の問題を考える際には平面で切って考えるのが基本です。


するとこのように↑正三角形に円がきれいに収まっているはずです。球の半径が $2$ であるとのことから、三角形の高さは $6$ であることが分かります。
というのも、この場合の円の中心は三角形の重心であり、重心の性質から
$\mathrm{AO}:\mathrm{OH}=2:1$
であるからです。
重心に気づかなくても解けるようになろう
数学は、重要な性質に気づけば楽に解ける場合が多いですが、気づかなくても解ける強引さも大事です。
重心に気づかない場合は強引に三平方の定理から求めます。
球の半径が $2$ であることより $\mathrm{OH}=2$ です。$\triangle\mathrm{OBH}$ は $60^\circ$, $30^\circ$, $90^\circ$ の直角三角形なので、
$$\mathrm{BH}=\sqrt{3}\mathrm{OH}=2\sqrt{3}$$
です。

そして、$\triangle\mathrm{ABH}$ も $30^\circ$, $60^\circ$, $90^\circ$ の直角三角形なので、
$$\mathrm{AH}=\sqrt{3}\mathrm{BH}=6$$
と求まります。

面積 $=$ 底辺 $\times$ 高さ
よって、正三角形の面積 $S$ は
$$S=4\sqrt{3}\times 6\div 2=12\sqrt{3}$$

体積 $=$ 底面積 $\times$ 高さ
よって、求める体積 $V$ は
$$V=12\sqrt{3}\times 4=48\sqrt{3}$$

三角柱の体積は、$48\sqrt{3}$
まとめ
内接円の高校入試問題を3つ見てきました。
近大和歌山の問題は接点までの距離は等しいという性質と三平方の定理より台形の高さを求めるのがキモでした。
四天王寺の問題も、接点までの距離は等しいという性質と三平方の定理からいろいろな長さが求められて生きました。加えて円周角の定理から円の中心を求めました。
最後の愛知県の問題は立体なので少し面食らう部分もあるかもしれませんが、立体も切ってしまえば平面です。どこで切るとよいのかを見極めるのが立体図形のキモです。


コメント