この記事は「等積変形と面積半分問題」シリーズの応用編です。基礎編で扱った「平行がミソの等積変形」と「底辺の中点で決まる面積半分」を土台に、より実戦的な問題を扱います。
図形の面積を半分に分ける直線を求める問題は、高校入試で頻出のテーマです。しかし、複雑な計算に時間を取られてしまい、解答にたどり着けない…そんな経験はありませんか？
この記事では、等積変形の考え方を使った“裏ワザ解法”を紹介します。面倒な面積計算を避けながら、三角形や四角形の面積半分問題をスッキリ解く方法を、例題付きで徹底解説します。
なお、等積変形を使った問題は単独の図形問題だけでなく、二次関数と絡めた入試問題でも頻出です。リンクは記事末尾にまとめてあります。また、基礎編をまだ見ていない方は先にこちらをどうぞ。
三角形の非頂点からの面積半分問題
頂点でない点から面積を半分にする問題です。基礎編で扱った「頂点からの面積半分」を応用することで、驚くほど楽に解けます。
問題
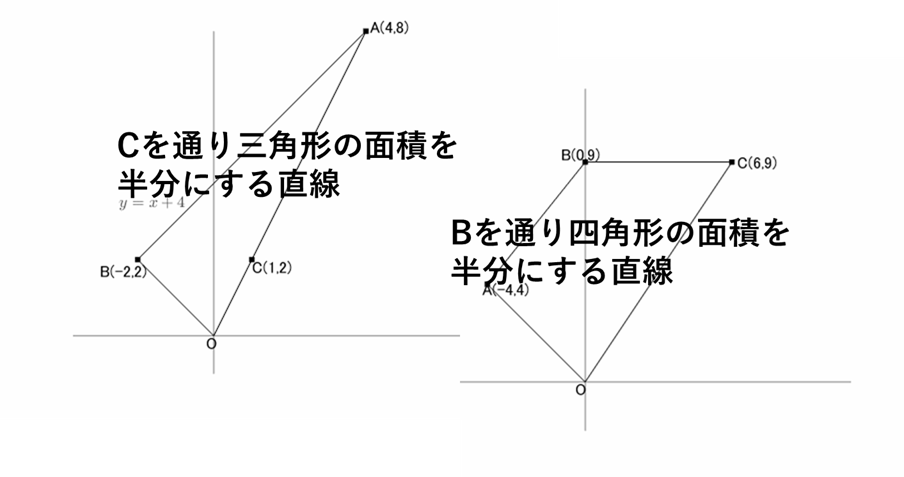
点 $\mathrm{C}$ を通り、$\triangle\mathrm{OAB}$ の面積を半分にする直線 $l$ の式を求めよ。
一気通貫アニメーション
解説
ステップ1：点 $\mathrm{O}$ を通る面積二等分線を考える
まず、点 $\mathrm{O}$ を通り $\triangle\mathrm{OAB}$ の面積を二等分する直線を考えます。目的は直線そのものではなく、その直線と辺 $\mathrm{AB}$ の交点 $\mathrm{M}$ を求めることです。点 $\mathrm{M}$ は明らかに辺 $\mathrm{AB}$ の中点なので、
$$\mathrm{M}(1,5)$$
ステップ2：$\mathrm{CM}$ を底辺に等積変形する
$\triangle\mathrm{OCM}$ に着目し、$\mathrm{CM}$ を底辺に等積変形すると $\triangle\mathrm{DCM}$ を得ます。
$\triangle\mathrm{OCM}$ の面積 ＝ $\triangle\mathrm{DCM}$ の面積
この部分は基礎編で扱った「平行がミソの等積変形」と同じ考え方です。
ステップ3：求める直線は $\mathrm{CD}$
等積変形したので、$\triangle\mathrm{DCA}$ は元の三角形の面積の半分です。
よって、求める直線は $\mathrm{CD}$ であり、その式は
$$l:y=-2x+4$$
練習問題
ここで一度、同じ構造の問題を自力で解いてみましょう。等積変形のイメージが一段と強固になります。
問題
点 $\mathrm{C}$ を通り、$\triangle\mathrm{OAB}$ の面積を半分にする直線 $l$ の式を求めよ。
一気通貫アニメーション
答え
$$l_1:\,y=-\displaystyle\frac{1}{7}x+\displaystyle\frac{30}{7}$$
四角形の面積半分問題：2つの解法で攻略
ここでは、四角形の面積半分問題を典型的な2つのアプローチで解いていきます。どちらも等積変形の考え方を使うと驚くほどスッキリ解けます。
問題
点 $\mathrm{B}$ を通り、四角形 $\mathrm{OABC}$ の面積を半分にする直線の方程式を求めよ。
解法1：一気通貫アニメーション
解法1：解説
ステップ1：四角形の面積比を考える（比だけでよい）
四角形の面積は、三角形に分けて考えると扱いやすくなります。今回は点 $\mathrm{B}$ が主役なので、次のように分けます。
面積を実際に求める必要はありません。比だけでよいです。底辺 $\mathrm{OB}$ が共通なので、面積比は高さの比になります。
$$4:6$$
しかし、今求めたいのは「半分」です。つまり、赤の領域（6）から青の領域（4）へ少しだけ面積を移動させればよい。
⑥＝①＋⑤ と分けて、①を青に移せばちょうど半分になります。
このようになる点 $\mathrm{M}$ を求めるには、$\mathrm{OC}$ を $1:5$ に分ければよいです。
求める直線は $\mathrm{BM}$ なので、傾きが $\displaystyle\frac{15}{2}$ であることに注意すると、
$$l:\;y=-\frac{15}{2}x+9$$
$$l:\;y=-\frac{15}{2}x+9$$
参考
面積配分の考え方は、下記の入試問題でも頻出です。
また、下記の頻出パターン5でも扱っています。
解法2：一気通貫アニメーション
解法2：解説
ステップ1：等積変形で四角形を三角形に変形する
底辺に平行に頂点を動かしても面積は変わりません(等積変形)。底辺を $\mathrm{OB}$ とみて、それぞれの頂点から平行線を引きます。
そして頂点を動かします。
すると、四角形 $\mathrm{OABC}$ の面積は $\triangle\mathrm{A^\prime BC^\prime}$ の面積と等しくなります。
この状態で、頂点 $\mathrm{B}$ を通り面積を二分するのは簡単です。
これを元の四角形に戻します。
点 $\mathrm{M}\left(1,\displaystyle\frac{3}{2}\right)$ が面積を二分する点です。よって求める直線は $\mathrm{BM}$ なので、
$$l:\;y=-\frac{15}{2}x+9$$
$$l:\;y=-\frac{15}{2}x+9$$
まとめ
面積半分問題の応用として、三角形の頂点でない点から面積を半分にする問題、そして四角形の面積を半分にする問題を扱いました。
どちらも、等積変形を使うことで驚くほど簡単に解けることがわかりました。一方で、実際に面積を計算して強引に解く方法もあります。ここでは、等積変形を使った“楽に解けるワザ”を身につけてください。
以上の問題は強引に解くこともできます。その方法は、下記の記事で扱っています（下記記事では「万能」と位置付けています）。
また、等積変形は二次関数と絡めた入試問題でも頻出です。例えば、下記の記事のパターン1で扱っています。
入試問題の具体例としては、下記の大阪星光学院や四天王寺の問題が参考になります。
コメント