ここで解いているのは一つ二つの問題ですが、それをいろいろな角度から眺め、解いています。このような勉強をやっていれば、点と点の知識が線で結ばれていきます。結構な難しい問題ではありますが、ここまでしゃぶり尽くせば円周角の定理の難しい問題も自信がつくはずです。ぜひここで述べている勉強法をしてもらいたいです。
しゃぶり尽くす問題はこれ
線分 $\mathrm{AD}$ の長さは?

これは、2025年度の四天王寺高校の入試問題で、下記↓で解説していますが、ここではこの問題をしゃぶり尽くします。
実際の入試問題ではこの問題は(3)で、問題文では $\mathrm{BC}=5$ が与えられており、まずは(1)で $\mathrm{BE}=2$ を答えさせるようになっています。また(2)では $\mathrm{AE}=x$, $\mathrm{ED}=y$ と置いた上で、$xy$ の値を問うています。

ここでは(1)の問いは飛ばし上記の図形から入り、(2)の $xy$ の値から求めます。
$xy$ の値はいくつか分かりますか? 方べきの定理より、
$$xy=6\tag{1}\label{p7698eq1}$$
です。方べきの定理は下記の記事↓で述べています。
さてこれよりこの問題をしゃぶり尽くしていきましょう。
しゃぶり尽くすために必要な基本の補助線と円周角の定理
一連の作業をアニメーションで確認します。
補助線
まずはこの形を見たら $\mathrm{BD}$ と $\mathrm{DC}$ に線を引きましょう。

円周角1
$$\angle\mathrm{DAC}=\angle\mathrm{DBC}$$
です。


円周角2
同様に、
$$\angle\mathrm{BAD}=\angle\mathrm{BCD}$$
です。


この2つから二等辺三角形であることが分かる
余談ですが、上記の円周角1,2から $\triangle\mathrm{BCD}$ は実は
二等辺三角形
であることが分かります。底角が等しいからですね。

円周角3
そして、今度は別のところの角度に着目することになりますが、同様に円周角の定理から
$$\angle\mathrm{CDA}=\angle\mathrm{CBA}$$
です。


最終的な基本状態
以上を踏まえ、問題文から下記の状態までは条件反射的に発想できるようになりましょう。

$\triangle\mathrm{DAB}\unicode[sans-serif]{x223D}\triangle\mathrm{DBE}$ に着目
$$\triangle\mathrm{DAB}\unicode[sans-serif]{x223D}\triangle\mathrm{DBE}$$
に着目します。

これは下記↓で解答としたものです。
裏返しの相似
裏返すと下図↓のようになります。

$$\triangle\mathrm{DAB}\unicode[sans-serif]{x223D}\triangle\mathrm{DBE}$$
より、
$$4:2=z:y=(x+y):z$$
\begin{eqnarray}
\therefore\left\{\begin{array}{l}
4y=2z\tag{2}\label{p7698eq2}\\
4z=2(x+y)
\end{array}
\right.
\end{eqnarray}
上式と下式から $z$ を消去すると、
\begin{eqnarray}
4y &=& x+y\\
\therefore\;3y &=& x
\end{eqnarray}
これを、方べきの定理より得られる式\eqref{p7698eq1}の
$$xy=6$$
に代入すると、
\begin{eqnarray}
3y^2 &=& 6\\
y^2 &=& 2\\
\therefore\;y &=& \sqrt{2}\; (>0)\\
\therefore\;x &=& 3\sqrt{2}\\
\therefore\;x+y &=& 4\sqrt{2}
\end{eqnarray}
$$\mathrm{AD}=4\sqrt{2}$$
$\triangle\mathrm{ADC}\unicode[sans-serif]{x223D}\triangle\mathrm{CDE}$ に着目
$$\triangle\mathrm{ADC}\unicode[sans-serif]{x223D}\triangle\mathrm{CDE}$$
に着目します。

裏返しの相似
裏返すと下図↓のようになります。

$$\triangle\mathrm{ADC}\unicode[sans-serif]{x223D}\triangle\mathrm{CDE}$$
より、
$$6:3=z:y=(x+y):z$$
\begin{eqnarray}
\therefore\left\{\begin{array}{l}
6y=3z\\
6z=3(x+y)
\end{array}
\right.
\end{eqnarray}
上式と下式から $z$ を消去すると、
\begin{eqnarray}
4y &=& x+y\\
\therefore\;3y &=& x
\end{eqnarray}
以下、前節と同じようにして
$$\mathrm{AD}=4\sqrt{2}$$
が得られる。
$\triangle\mathrm{ADC}\unicode[sans-serif]{x223D}\triangle\mathrm{ABE}$ に着目
$$\triangle\mathrm{ADC}\unicode[sans-serif]{x223D}\triangle\mathrm{ABE}$$
に着目します。

回転の相似
回転すると下図↓のようになります。

$$\triangle\mathrm{ADC}\unicode[sans-serif]{x223D}\triangle\mathrm{ABE}$$
より、
\begin{eqnarray}
6:x &=& (x+y):4\\
x(x+y) &=& 24\\
\end{eqnarray}
これと、方べきの定理より得られる式\eqref{p7698eq1}の
$$xy=6$$
から、
\begin{eqnarray}
x^2+6 &=& 24\\
x^2 &=& 18\\
\therefore\; x &=& 3\sqrt{2}\,(>0)
\end{eqnarray}
さらに、$xy=6$ とから、
$$y=\sqrt{2}$$
よって、$x+y=4\sqrt{2}$。以上より、
$$\mathrm{AD}=4\sqrt{2}$$
が得られる。
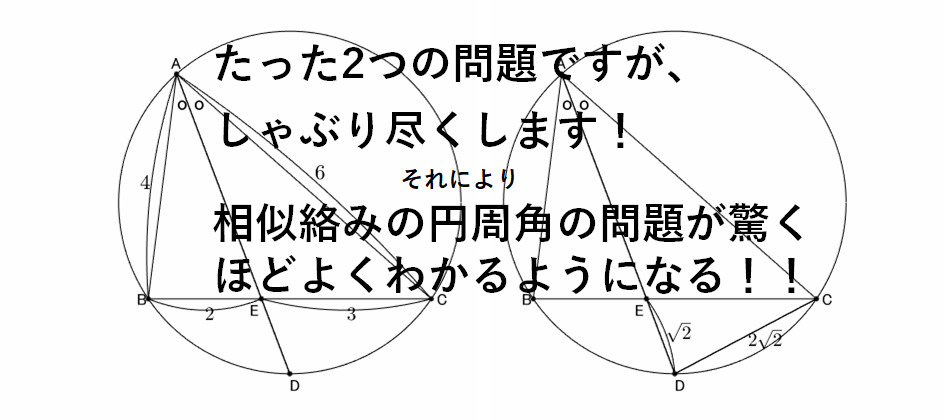
結局こうなった
\eqref{p7698eq2}から $z=2y=2\sqrt{2}$ も分かるので、結局、左の図から相似を駆使することで右の図が得られました。


左の図を出発点にして右の図が得られるよう、それもこれら3種類で得られるよう、何度も何度も繰り返し練習することにより、他の問題に出会ったときにでも解く着想が容易に得られるようになります。
もう一つしゃぶる
さて、同じ図形ですがもう一つ、別の味を試してみましょう。
$\mathrm{AB}\times\mathrm{AC}$ は?

答えはこの図形から $24$ ですが、それを求めます。
今回は $\mathrm{AB}\times\mathrm{AC}$ を求めよ、ということであり、$\mathrm{AB}$, $\mathrm{AC}$ を個別に求める必要はないというところが一つミソではあります。
これまで見てきたようにこの図形には相似が3つも隠れています。その中で $\mathrm{AB}$ や $\mathrm{AC}$ が含まれる三角形に着目しましょう。
$\triangle\mathrm{ADC}\unicode[sans-serif]{x223D}\triangle\mathrm{ABE}$ に着目
$$\triangle\mathrm{ADC}\unicode[sans-serif]{x223D}\triangle\mathrm{ABE}$$

より、
\begin{eqnarray}
\mathrm{AD}:\mathrm{AB} &=& \mathrm{AC}:\mathrm{AE}\\
\mathrm{AD}\times\mathrm{AE} &=& \mathrm{AB}\times\mathrm{AC}\tag{3}\label{p7698eq3}\\
\end{eqnarray}
求めたい $\mathrm{AB}\times\mathrm{AC}$ が右辺に出てきました。一歩近づいた感じです。しかし左辺の $\mathrm{AD}$ や $\mathrm{AE}$ は分かっていません。$\mathrm{ED}$ は分かっているのに、惜しい限りです。
相似は3つあったので、もう一つ作ってみます。今度は $\mathrm{AD}$ や $\mathrm{AE}$ が表れそうな図形を選びます。
$\triangle\mathrm{ADC}\unicode[sans-serif]{x223D}\triangle\mathrm{CDE}$ に着目
$$\triangle\mathrm{ADC}\unicode[sans-serif]{x223D}\triangle\mathrm{CDE}$$

より、
\begin{eqnarray}
\mathrm{AD}:\mathrm{CD} &=& \mathrm{CD}:\mathrm{DE}\\
\mathrm{AD}\times\mathrm{DE} &=& (\mathrm{CD})^2\\
\mathrm{AD}\times\sqrt{2} &=& (2\sqrt{2})^2\\
\therefore\;\mathrm{AD} &=& 4\sqrt{2}\\
\therefore\;\mathrm{AE} &=& 3\sqrt{2}\;(\because\mathrm{ED}=\sqrt{2})\tag{4}\label{p7698eq4}
\end{eqnarray}
これらの式より答えが出る
\eqref{p7698eq3}, \eqref{p7698eq4} より、
\begin{eqnarray}
\mathrm{AB}\times\mathrm{AC} &=& \mathrm{AD}\times\mathrm{AE}\\
&=& 4\sqrt{2}\times 3\sqrt{2}\\
&=& 24
\end{eqnarray}
$$\mathrm{AB}\times\mathrm{AC}=24$$
ダメ押しでもう一つしゃぶる
$?$ を求めよ。

ここまでで長くなりましたので、この回答は下記の記事↓に譲ります。
まとめ
一つの問題をいろいろな角度から眺め、しゃぶり尽くしました。本来、勉強とはこうあるべきで、一つの物事というのはいろいろな角度から見ることができる、ということをこのように身をもって理解するとともに、そのテクニックも身につけるということです。
そうすれば少し問いかけが異なるだけの類題などはたちどころに解けます。発想の近しい問題も難なく解けるようになります。また、いろいろな知識の点と点が線で結ばれ、絶対に忘れない強固で発想豊かな知識になります。
たくさんの問題をやみくもにこなすより、このように一つの問題をしゃぶり尽くす勉強を、是非してもらいたいです。




コメント