ここでは頂点でない点を通る直線により三角形の面積を半分にする問題を扱います。一つ目は、高校入試を強く意識した解き方で最も楽に解けます。でも解き慣れていないと難しいかもしれません。そのような場合でも二つ目、三つ目の解き方で解けるようになれば、真に実力があるといえると思います。
問題:頂点でない点を通る直線により三角形の面積を半分にする
点 $\mathrm{C}(0,2)$ を通り、$\triangle\mathrm{OAB}$ の面積を二等分する直線は?

$\triangle\mathrm{OAB}$ の面積は当然答えられるように
まず、三角形 $\triangle\mathrm{OAB}$ の面積は $3$ であることは、問われればすぐに答えられるようにしましょう。
\begin{eqnarray}
\triangle\mathrm{OAB} &=& \frac{1}{2}\times 2\times 3\\
&=& 3
\end{eqnarray}
です。

点 $\mathrm{C}$ を通り $\triangle\mathrm{OAB}$ の面積を二等分にする直線のイメージ
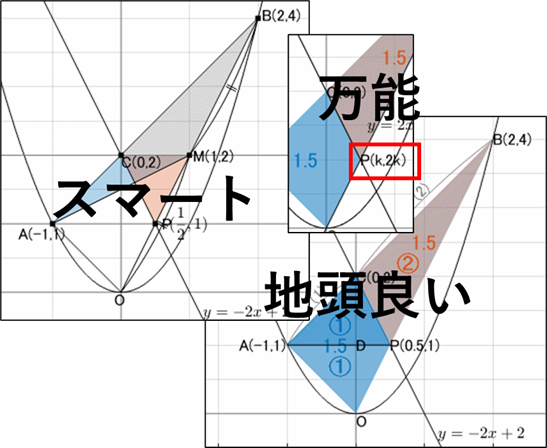
面積が $3$ ということは、それを半分にしたいのでそれぞれ $1.5$ ずつに分けたいということです。このイメージ図↓を再生すれば直線が彷徨っていますが、ここで表現したいのは、直線が決まれば(直線を決めれば)面積は決まる、ということです。この発想は特に「解き方3. 強引な解き方」で述べます。
解き方1. 高校入試っぽい解き方
解
$\mathrm{OB}$ の中点を $\mathrm{M}$ と置くと $\mathrm{M}(1,2)$ であり、このとき
$\triangle\mathrm{MAB}$ は $\triangle\mathrm{OAB}$ の半分
である。

ここで、点 $\mathrm{A}$ を通り $\mathrm{CM}$ に平行な直線を引き、線分 $\mathrm{OB}$ と交わる点を $\mathrm{P}$ と置くと、
$\triangle\mathrm{ACM}$ の面積 $=$ $\triangle\mathrm{PCM}$ の面積(下図)
なので、
$\triangle\mathrm{PCB}$ の面積は $\triangle\mathrm{OAB}$ の面積の半分

よって、直線 $\mathrm{CP}$ を求めればよいから、求める直線の式は、
$$y=-2x+2$$

解説1-1. 詳しくはこちら
この解き方は下記の記事↓で詳しく解説しています。
解き方2. 地頭のよい解き方
四角形は三角形2つです。四角形の面積は三角形2つの面積の和です。この発想から、考える図形をすべて三角形に分割してしまえば、面積比は割と簡単に考えられます。
解
明らかに $\triangle\mathrm{OAC}<\triangle\mathrm{OBC}$ より、点 $\mathrm{P}$ は線分 $\mathrm{OB}$ 上にある。
このとき、
$\mathrm{AP}$ で 四角形 $\mathrm{OACP}$ を分ける。すると、
$\mathrm{AC}:\mathrm{CB}=1:2$ より、
$\triangle\mathrm{OAB}$ は下図のように分けられることになる。

すなわち
$$\mathrm{OD}:\mathrm{DC}=1:1$$
であり、$\mathrm{OC}=2$ より、
$$\mathrm{OD}=\mathrm{DC}=1$$
$$\therefore\;\mathrm{D}(0,1)$$
よって、$\mathrm{P}$ の $y$ 座標は $1$ であることが分かり、
直線 $\mathrm{OB}$ は $y=2x$ であるから、
$$\mathrm{P}(\displaystyle\frac{1}{2}, 1)$$
よって、求める直線 $\mathrm{CP}$ は、
$$y=-2x+2$$
解説2-1. $\triangle\mathrm{OAB}$ を分割する発想について
分割する支点(この場合の点 $\mathrm{C}$)が頂点でない場合は片一方が四角形になってしまいますが、四角形を三角形2つに分けて考えるとうまくいく場合が多いです。
今回の場合では $\triangle\mathrm{OAB}$ を二等分したいわけですが、
$$\mathrm{AC}:\mathrm{CB}=1:2$$
なので、
$$\triangle\mathrm{ACP}:\triangle\mathrm{BCP}=1:2$$
です。すると、残りの $\triangle\mathrm{OAP}$ があと $1$ の面積を受け持ってくれればいいことが分かります。
従って、『$\triangle\mathrm{OAB}$ は下図のように分けられることになる。』という回答の文言になります。

類題
近しい解き方をしている類題に下記↓があります。
直接その箇所へはこちら。この問題は、四角形全体の面積が⑩なので、半分にするには⑤と⑤に分ける、という発想をしています。
直接その箇所へはこちら。この問題は、台形の面積比をその底辺の長さの比で置き換えて考えているところがミソです。
解き方3. 万能な解き方
これは万能ですが強引です。強引ですが万能、という方がよいかもしれません。強引に解けるというのは絶対に解きたい入試の場面においては結構使えます。解き方1,2のようなスマートな解き方はもちろんですが、こういった力もつけていきたいです。
解
明らかに $\triangle\mathrm{OAC}<\triangle\mathrm{OBC}$ より、点 $\mathrm{P}$ は線分 $\mathrm{OB}$ 上にある。すなわち、$y=2x$ 上にある。従って、点 $\mathrm{P}$ の座標は
$$\mathrm{P}(k,2k)$$
と置ける。

このとき、
\begin{eqnarray}
\triangle\mathrm{PBC} &=& \triangle\mathrm{OBC}-\triangle\mathrm{OPC}\\
&=& 2\times 2\times\frac{1}{2}-2\times k\times\frac{1}{2}\\
&=& 2-k
\end{eqnarray}
これが $\triangle\mathrm{OAB}$ の面積 $3$ の半分になればよいから、
\begin{eqnarray}
2-k &=& \frac{3}{2}\\
\therefore\; k&=&\frac{1}{2}
\end{eqnarray}
よって、
$$\mathrm{P}(\displaystyle\frac{1}{2}, 1)$$
ゆえに、求める直線 $\mathrm{CP}$ は、
$$y=-2x+2$$
解説3-1. パラメータ表示に慣れると強い
解答では求める点 $\mathrm{P}$ の座標を
$$\mathrm{P}(k,2k)$$
と置きました。これは、点 $\mathrm{P}$ が直線 $y=2x$ 上にあるためで、仮に点 $\mathrm{P}$ の $x$ 座標を $x=k$ だとすると、$y$ 座標は $y=2k$ となるためです。
このように、ある直線や図形上の点を、$k$ などといった $x$, $y$ とは異なる文字を介して表現する方法を
- パラメータ表示
または日本語で
- 媒介変数表示
と言います。強引解法の強い味方です。ぜひ練習してみてください。
類題
近しい解き方をしている類題に下記↓があります。直接その箇所へはこちら。
おまけ. 一応公式的なものはある
分割する支点が頂点でない場合でも、一応公式的なものはあります。それは、
$$\triangle\mathrm{BCP}:\triangle\mathrm{BAO}=\mathrm{BC}\times\mathrm{BP}:\mathrm{BA}\times\mathrm{BO}$$
です。今回のケースに当てはめれば $\triangle\mathrm{BCP}:\triangle\mathrm{BAO}=1:2$ にしたいので、
\begin{eqnarray}
\begin{array}{c}
1:2 = 2\times\mathrm{BP}:3\times\mathrm{BO}\\
\mathrm{BP}:\mathrm{BO} = 3:4\\
\therefore\;\mathrm{BP}:\mathrm{PO} = 3:1
\end{array}
\end{eqnarray}
となり、$\mathrm{P}$ の座標が
$$\mathrm{P}(\,\displaystyle\frac{1}{2}, 1\,)$$
と求まります。
しかし、この公式はそれほど出番も多くないため、これまで述べたような考え方をマスターする方をおススメします。
まとめ
頂点でない点を通る直線により三角形の面積を半分にする問題を扱いました。一番目の解き方は最も楽に解けるものであり、高校入試問題を解く上では最も推奨できます。でも、この解き方は少しテクニカルであり、入試問題に慣れていない人には思いつかないかもしれません。そのような場合でも、二つ目や三つ目の解き方で解けるような実力をつければ、この問題だけではなくいろいろなところで役に立ちますので、一つの問題を解く際にも複数の解き方が思いつくような勉強法を普段からしていけるとよいと思います。
面積半分問題は下記記事でじっくりと取り組んでいます。


コメント