図形の問題って、個々の性質は理解できても、補助線を要したり組み合わされたりすると途端に難しいですよね。「答えを見たら理解はできるけど、自分では思いつかないよ、その補助線」みたいな感じです。そのような人はもう一歩です。発想法をスタートにして、発想法の引き出しをたくさん持っておくことで思いつくようになります。
このシリーズでは、平面図形の問題を、発想法の視点からまとめていきます。まずは流し読みでかまいません。発想法の引き出しを作っていくことが重要です。発想法のイメージをしっかりと頭に焼き付けられるよう、アニメーションを活用ください。発想法の引き出しがある程度できてから自分で考えて解いていく、この順番が一番効率的です。
また逆に、そのような発想法を全く無視して強引に解ける問題も少なくないです。入試では必ずしも美しく解く必要はないので、最後の手段としてそのような強引な手法も持ち合わせていると強いです。シリーズの中ではそこにも言及していきます。
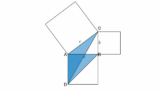
問題1：直角三角形から円が見える
？の角度を求めよ。
イメージ：どんどんと二等辺三角形が明らかに
まずはアニメーションで全体のイメージをつかんでください。また、復習の際にはアニメーションだけを見てもよいでしょう。頭の中でアニメーションが自動再生されるようになれば、自分の引き出しにできた合図です。
解
$\triangle\mathrm{BAD}$ で $\angle\mathrm{A}=90^\circ$ であることより、$\mathrm{BD}$ の中点を $\mathrm{O}$ とすると
$$\mathrm{AO}=6\mathrm{cm}$$
なので、$\triangle\mathrm{AOB}$ は二等辺三角形となる。
よって、$\angle\mathrm{OAB}=15^\circ$。
ここで、$\angle\mathrm{BAD}=90^\circ$ より、
$\angle\mathrm{OAD}=75^\circ$
また、$\triangle\mathrm{AOD}$ は二等辺三角形なので $\angle\mathrm{ODA}=75^\circ$ となるから、
$\angle\mathrm{AOD}=30^\circ$
さらに、$\triangle\mathrm{OAC}$ は二等辺三角形なので、
$\angle\mathrm{ACD}=30^\circ$
解説：円とのコラボ_直角三角形を見たら二等辺三角形を作ろう
直角の頂点から中線を引くと二等辺三角形が二つできます。下記のように二通りの見方で理解できます。
一つは外接円を考えることです。$\angle\mathrm{A}=90^\circ$ より $\triangle\mathrm{BAD}$ には外接円が書けます。すると $\mathrm{BD}$ の中点 $\mathrm{O}$ は外接円の中心になっており、線分 $\mathrm{OA}$, $\mathrm{OB}$, $\mathrm{OC}$ は全て円の半径なので長さは等しいです。
もう一つは同じ図形を回転してくっつけることです。すると四角形 $\mathrm{ABED}$ は長方形になります。長方形の対角線は中点で交わるため、長さは等しいです。
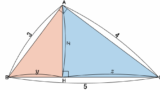
問題2：半径から円が見える
$a$ を求めよ。
これは問題1の逆バージョンです。$\mathrm{OA}=\mathrm{OB}=\mathrm{OC}$ から $\angle\mathrm{BAC}=90^\circ$ を見抜けるかがポイントです。直角三角形が見抜ければ三平方の定理を使うのは定石ですが、これは三年生で学習するので未学習の人は予習のつもりで見てください。
なお、三平方の定理については↓に小学生にも分かる証明アニメーションがあります。
イメージ：コンパスで円を書く
角の二等分線の性質を使った後、コンパスのようなシーンが出てきます。ここがこの問題のミソです。図形パターンとコンパスイメージを焼き付けましょう。
解
$\mathrm{DC}=x$ と置く。
線分 $\mathrm{BD}$ は $\angle\mathrm{ABC}$ の二等分線なので、
\begin{eqnarray}
6:2a &=& 3:x\\
\therefore\; x &=& a
\end{eqnarray}
また、$\mathrm{OA}=\mathrm{OB}=\mathrm{OC}$ より $\triangle\mathrm{ABC}$ は点 $\mathrm{O}$ を中心とする円に内接する。すなわち、
$$\angle\mathrm{BAC}=90^\circ$$
よって三平方の定理より、
\begin{eqnarray}
6^2+(3+a)^2 &=& (2a)^2\quad (\because\; x=a)\\
3a^2-6a-45 &=& 0\\
3(a-5)(a+3) &=& 0
\end{eqnarray}
$a>0$ より、
$$a=5$$
まとめ
直角三角形から二等辺三角形を連想するなんてなかなかのものですが、外接円を仲介することで連想できますね。一つ一つは教科書レベルの簡単な発想ですが、それが組み合わさると途端に難問になります。このシリーズではこのような発想の引き出しを養っていくので、今後も見てください。例えば↓はたいていの人は相似を使って解くけど実はもっと簡単な方法があるよ、という記事です。直角三角形なのでやはり外接円が登場します。
コメント