円周角の定理の高校入試問題です。発想のポイントは角度が移動する、というところです。それにより特殊な直角三角形や相似が見えてきます。
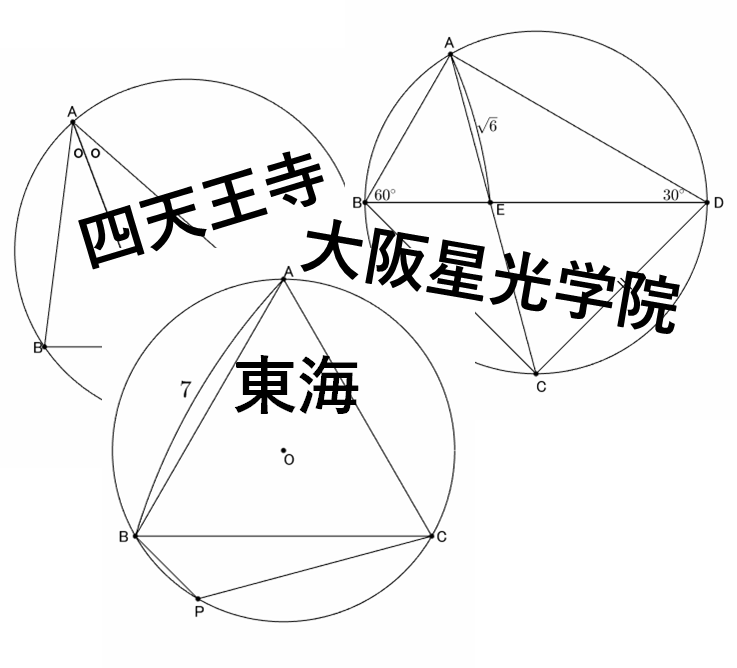
四天王寺高校 2025年度
この問題は下記で解説をするのですが、別解含めて別の記事でも解説していますので、これを読んだ後にはこちら↓も読むことで理解が厚くなります。
問題
$\mathrm{AB}=4$, $\mathrm{BC}=5$, $\mathrm{CA}=6$ である。$\mathrm{AE}=x$, $\mathrm{DE}=y$ とおく。
(1) 線分 $\mathrm{BE}$ の長さを求めよ。
(2) $xy$ の値を求めよ。
(3) 線分 $\mathrm{AD}$ の長さを求めよ。

解答を一気通貫アニメーションで
初見では全く分からないと思いますので、以下にステップバイステップで見ていきます。
(1) 解説
角の二等分線を見たら・・・
$\mathrm{AD}$ は $\angle\mathrm{BAC}$ の二等分線なので、
$$\mathrm{AB}:\mathrm{AC}=\mathrm{BE}:\mathrm{EC}$$
です。よって、下図のようになります。

$\mathrm{BC}=5$ を $4:6(=2:3)$ に分割するので、$\mathrm{BE}$, $\mathrm{EC}$ の長さはそれぞれ $2$, $3$ となります。

$$\mathrm{BE}=2$$
下記の記事↓で「角の二等分線の発想」を鍛えてください。
(2) 解説
積が分かればよい、ということは・・・
そうです。方べきの定理が使えます。方べきの定理は下記の記事↓で解説しています。
よって、すぐさま下図のように適用できます。

$$xy=6$$
(3) 解説
あと使っていない条件は・・・
$\triangle\mathrm{ABC}$ が円に内接している、ということです。円周角の定理が使えます。
円周角の定理は角度を移動させるのに使います。
$$\angle\mathrm{CAD}=\angle\mathrm{CBD}$$
です。


この形を見たら・・・
この形というのは↓です。

言語化するならば、
一つの角が共通で、他の角が同じ角度の二つの三角形
ここまで言語化できればもうその二つの三角形は相似であることは分かりますね。
下記の記事↓の発想です。これの「初級」です。
裏返しの相似
裏返すと下図↓のようになります。ここで、$\mathrm{BD}=z$ と置きました。

$$\triangle\mathrm{DAB}\unicode[sans-serif]{x223D}\triangle\mathrm{DBE}$$
より、
$$4:2=z:y=x+y:z$$
\begin{eqnarray}
\therefore\left\{\begin{array}{l}
4y=2z\\
4z=2(x+y)
\end{array}
\right.
\end{eqnarray}
上式と下式から $z$ を消去すると、
\begin{eqnarray}
4y &=& x+y\\
\therefore\;3y &=& x
\end{eqnarray}
これを、(2)の解答である
$$xy=6$$
に代入すると、
\begin{eqnarray}
3y^2 &=& 6\\
y^2 &=& 2\\
\therefore\;y &=& \sqrt{2}\; (>0)\\
\therefore\;x &=& 3\sqrt{2}\\
\therefore\;x+y &=& 4\sqrt{2}
\end{eqnarray}
(3) の問題は、線分 $\mathrm{AD}$ の長さを求めよであり、これは $x+y$ なので、$4\sqrt{2}$ です。
$$\mathrm{AD}=4\sqrt{2}$$
別解:この問題をしゃぶり尽くして達人へ
下記↓の記事ではこの問題を3つの解き方で解いています。また、同じ図形ですが問題を少し変えた類題を出しています。一つの問題をしゃぶり尽くす理想の勉強法です。
大阪星光学院高校 2024年度
問題
円の半径と $\mathrm{CE}$ の長さを求めよ。

解答を一気通貫アニメーションで
初見では全く分からないと思いますので、以下にステップバイステップで見ていきます。
解説
$60^\circ$ と $30^\circ$ から直角三角形がピンとくる
まず、$\angle\mathrm{ABD}=60^\circ$, $\angle\mathrm{ADB}=30^\circ$ より、
$$\angle\mathrm{A}=90^\circ$$
であることが分かります。これが分かると同時に
$\mathrm{BD}$ は直径
であることも分かります。
問題文の条件 $\mathrm{BC}=\mathrm{CD}$ は角度が同じことを物語る
そして問題文の条件から、
$$\mathrm{BC}=\mathrm{CD}$$
であることより、
$$\angle\mathrm{BAC}=\angle\mathrm{DAC}=45^\circ$$
であることが分かります。

弧の長さは円周角の大きさ、です。
$45^\circ$ と $60^\circ$ の三角形を見たら・・・
そうすると $\triangle\mathrm{ABE}$ は $45^\circ$ と $60^\circ$ を持つ三角形ということになります。この三角形を見たら
かの有名な直角三角形が2つくっついたもの!
ということにピン!と来てください。
下の図で青の直角三角形から各辺の長さが分かります。

同様に赤の直角三角形からも各辺の長さが分かります。

半径が分かった!
これで $\mathrm{AB}$ の長さが分かりましたが、これは下記の正三角形から実は求めるべき半径です。

半径は、$\sqrt{3}+1$
$\mathrm{ED}$ はすぐに分かるから・・・
半径が分かったので、$\mathrm{ED}$ はすぐに分かり、
$$\mathrm{ED}=2\sqrt{3}$$
です。なぜなら、$\mathrm{BE}=2$ であり、これと合わせて直径($=2(\sqrt{3}+1)$)だからです。
あとは方べきの定理
よって、方べきの定理より、
\begin{eqnarray}
\sqrt{6}\times\mathrm{EC} &=& 2\times\mathrm{2\sqrt{3}}\\
\therefore\;\mathrm{EC} &=& 2\sqrt{2}
\end{eqnarray}

$$\mathrm{EC}=2\sqrt{2}$$
東海高校 2024年度
問題
図のように、1辺の長さが $7\mathrm{cm}$ である正三角形$\mathrm{ABC}$ が円 $\mathrm{O}$ に接している。点 $\mathrm{P}$ は弧 $\mathrm{BC}$ 上を動き、$\angle\mathrm{BPC}=120^\circ$ である。
(1) 円 $\mathrm{O}$ の半径は [ ] $\mathrm{cm}$ である。
(2) $\angle\mathrm{BAP}=15^\circ$ のとき、$\mathrm{CP}=$ [ ] $\mathrm{cm}$ である。

(3) はかなり難問なので、ここでは省略。
解答を一気通貫アニメーションで
初見では全く分からないと思いますので、以下にステップバイステップで見ていきます。
(1) は確実に解きたい
どの問題も大抵 (1) は優しいです。これも、正三角形の1辺が $7\mathrm{cm}$ と言っているので、その高さは容易に分かり、そこから半径は容易に分かります。
(1)の解答をアニメーションで眺めます。
(1) 解説
正三角形の1辺の長さから高さを求める
頂点 $\mathrm{C}$ から辺 $\mathrm{AB}$ に垂線を下すとこれは円の中心 $\mathrm{O}$ を通り、$60^\circ$, $30^\circ$, $90^\circ$ の直角三角形になります。
$\mathrm{AH}$ は一辺 $7$ の半分なので、$\displaystyle\frac{7}{2}$。あとは直角三角形の辺の比から $\mathrm{CH}=\displaystyle\frac{7\sqrt{3}}{2}$ です。

点 $\mathrm{O}$ は重心
半径は $\mathrm{CO}$ ですが、これは、$\mathrm{CH}$ の $\displaystyle\frac{2}{3}$ です。なぜなら、$\mathrm{O}$ は正三角形の重心なので。ここで、重心の大事な性質をおさらいしておくと、
三角形の重心は、各中線の交点であり、各中線を2:1に内分する
です。よって、求める半径 $r$ (と勝手に置きました) は、
$$r = \frac{7\sqrt{3}}{2}\cdot\frac{2}{3}=\frac{7\sqrt{3}}{3}$$

(1)の答え、$\displaystyle\frac{7\sqrt{3}}{3}$
(2) はやや難だが、$ 15^\circ$ ときたらピンと来たい、あの角度
図形問題で $30^\circ$, $45^\circ$, $60^\circ$ はおそらく誰もがピンとくる角度です。ここで $15^\circ$ にもピンとくるのはかなりセンスがいいです。$30^\circ$, $45^\circ$, $60^\circ$ は $15^\circ$ ずつ増えています。今回になぞらえれば、
$$60^\circ-15^\circ=45^\circ$$
であり、$60^\circ$ と $15^\circ$ からピンとくる $45^\circ$ が生まれます。
さらに言えば、$45^\circ$ は $90^\circ$ の半分です。円が出てきたときには倍半分の角度にもピンとくるように練習を積むと実力が養われます。
(2)の解答をアニメーションで眺めます。
(2) 解説
問題文より $\angle\mathrm{BAP}=15^\circ$ なので、$\angle\mathrm{PAC}=45^\circ$ です。
そうすると、$\angle\mathrm{PAC}$ に対応する中心角は $\angle\mathrm{POC}$ であり、$90^\circ$ です。
つまり、$\triangle\mathrm{PAC}$ は直角三角形でありますが、同時に二等辺三角形でもあります。なぜなら $\mathrm{OC}$, $\mathrm{OP}$ はともに半径であり長さが等しいからです。
半径は (1) より $\displaystyle\frac{7\sqrt{3}}{3}$ と分かっているので、直角二等辺三角形の辺の比より $\mathrm{CP}$ は求まります。
$$\mathrm{CP}=\frac{7\sqrt{3}}{3}\cdot\sqrt{2}=\frac{7\sqrt{6}}{3}$$

(2)の答え、$\displaystyle\frac{7\sqrt{6}}{3}$
(2) の別解
$\angle\mathrm{APC}$ は $60^\circ$ ということに気づくでしょうか。円周角の定理から $\angle\mathrm{ABC}$ と同じ角度だからです。これに気づくと $\triangle\mathrm{APC}$ は直角定規を2つくっつけた三角形であることに気づくでしょう。上でみた星光学院の問題と同じ形状です。
(2) の別解の解説
円周角の定理より
$$\angle\mathrm{APC}=\angle\mathrm{ABC}=60^\circ$$
です。

$\triangle\mathrm{APC}$ は直角三角形の定規を2つ組み合わあせた図形なのでその長さは容易に分かります。$\mathrm{AC}=7$ であることと、直角二等辺三角形(下記青三角形)より、他辺の長さは
$$\frac{7\sqrt{2}}{2}$$
です。

そうすると、他方の直角三角形の辺の比より、
$$\mathrm{CP}=\frac{7\sqrt{2}}{2}\cdot\frac{1}{\sqrt{3}}\cdot2=\frac{7\sqrt{6}}{3}$$
と求まります。

(2)の答え、$\displaystyle\frac{7\sqrt{6}}{3}$
まとめ
円周角の定理の高校入試問題を見てきました。円周角の定理の高校入試問題的発想としては角度が移動する、というところです。同じ弧を持つ円周角は等しいというところは、言い換えれば一方の角度が分かっていれば他方も分かる(同じなので)ということで、角度が移動する感覚です。
移動した結果、特殊な直角三角形が見えてきたり、相似が見えてきたしします。これらの発想を自由に行き来できるようになるよう、練習を積んでください。下記の記事↓で骨太の理解ができます。
また、今回の例はいずれも円がある中で円周角の定理を使う問題でしたが、円が無い状態から円周角の定理が見えてほしい逆引き的な例もあります↓。この機会に引き出しを増やしておきましょう。






コメント