【内接円：実践】公式をマスターしたら実際の問題で適用方法を確認！

　公式は前稿で解説していますが、覚えるのではなく考え方をマスターしてください。ここではその考え方が実際の問題にきちんと応用できるかを確認します。前稿はこちら↓。

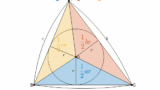
面積と3辺の長さを元に内接円の半径を求める

問題

　これの基本形は前回の投稿の公式で学びましたが、その際には面積が既知であるとしました。なので、面積さえ求められれば基本形であると理解できます。直接該当箇所はこちら。

面積を求めるのも、実は基本形です。直接該当箇所はこちら。

一気通貫アニメーション

　このアニメーションが頭の中で再生されるようになると、強いです。

解説

　公式は覚える必要はありませんが、面積が必要だったな、ということは思い出したいです。その意味で何となくの公式の形は覚えておいた方がよいかもしれません。

なのでまずは面積を求めます。

三平方の定理を用いて高さを求める

　3辺が分かっているときの面積は三平方の定理を用いて高さを求めることで求められます。

頂点 $\mathrm{A}$ から辺 $\mathrm{BC}$ に垂線 $\mathrm{AH}$ を下ろし、$\mathrm{AH}$ を2つの直角三角形の三平方の定理で表現します。

$$13^2-x^2=\mathrm{AH}^2=15^2-(14-x)^2$$

これを $x$ について解きます。そのまま解くと計算が面倒なので、少し工夫します。

$a^2-b^2=(a+b)(a-b)$ の因数分解を用いて計算を工夫する

\begin{eqnarray}
13^2-x^2 &=& 15^2-(14-x)^2\\
(14-x)^2-x^2 &=& 15^2-13^2\\
\{(14\cancel{-x})\cancel{+x}\}\{(14-x)-x\} &=& (15+13)(15-13)\\
14\,(14-2x) &=& 28\times 2\\
\cancel{14}(14-2x) &=& 2\,\cancel{28}\times 2\\
14-2x &=& 4\\
-2x &=& -10\\
x &=& 5
\end{eqnarray}

長くにはなってしまいましたが、$15^2$ や $14^2$ や $13^2$ をまともに扱うよりもずっと楽です。

$x=5$ と求まったので、

\begin{eqnarray}
\mathrm{AH}^2 &=& 13^2-5^2\\
&=& (13+5)(13-5)\\
&=& 18\times8\\
&=& (9\times 2)\times (4\times 2)\\
&=& 3^2\times 2^2\times 2^2\\
\therefore\; \mathrm{AH} &=& 3\times 2\times 2\\
&=& 12
\end{eqnarray}

ここは計算で求めましたが、特別な直角三角形を思い出せば、計算しなくてもすぐに分かります。

高さが求まったので面積を求める

　高さが $\mathrm{AH}=12$ と求まったので面積が求められます。

$$S=14\times 12\div 2=84$$

面積が求まったので内接円の半径を求める

　公式を覚えるよりは次の式を立てられるようになる方が有益です。

$$S=84=\frac{1}{2}\, 14\, r+\frac{1}{2}\, 15\, r+\frac{1}{2}\, 13\, r$$

ここから $r$ を解いて、

$$r=4$$

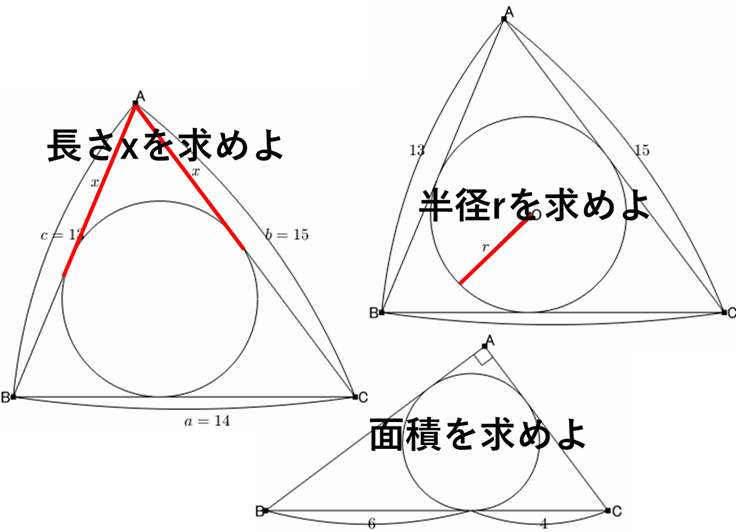
3辺の長さを元に頂点から接点までの距離を求める

問題

これも公式を示せば

ですが、導き方を理解しましょう。

一気通貫アニメーション

解説

求めたい $x$ を含む辺の和：

ここから対面の辺を引くと、

余分な $y$ と $z$ がきれいに消えてくれて、$2x$ だけが残ります。すなわち、

$$15+13-14=2x$$

となり、$x=7$ が求まります。

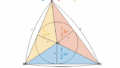
直角三角形の場合は三平方の定理を使う

問題

上の問題の発展形です。3辺の長さが分かっているわけではありませんが、その代わりに直角三角形であるとなっているため、三平方の定理を用いるのであろうと想像できます。

解説

　他の辺は、$x$ を用いることにより下記のように表せます。

これに三平方の定理を適用して、

\begin{eqnarray}
(x+6)^2+(x+4)^2 &=& 10^2\\
(x^2+12x+36)+(x^2+8x+16) &=& 100\\
2x^2+20x+52 &=& 100\\
x^2+10x-24 &=& 0\\
(x+12)(x-2) &=& 0\\
\therefore\; x=2\;\;(\because x>0)
\end{eqnarray}

ゆえに、三角形の面積は、

$$S=8\times 6\div 2=24$$

これはなんと $ 6\times 4$ だった

　これも、公式を覚えておく必要はありません。数学の美しさに感動するだけで充分です。これの計算による証明と、図形による鮮やかな証明は下記の記事↓で述べています。直接該当箇所はこちら。

まとめ

　公式編↓で学んだ知識を具体的な問題で確認しました。

公式とはいっても覚えるのではなく都度導いて使うように心がけましょう。