高校入試数学で頻出する「等積変形」と「面積半分問題」。図形の面積を扱う問題は、解法のパターンを理解すれば一気に得点源になります。本記事では、等積変形の基本原理から面積半分問題の解き方まで、図を使ってわかりやすく解説。入試対策や定期テストの復習に役立つ内容です。
等積変形とは
平行線が見やすい基本形
等積変形とは、面積を同じ状態で図形を変形させることです。高校入試の文脈では主に下記のアニメーションのように、三角形の面積を同じくする変形を指すことが多いです。
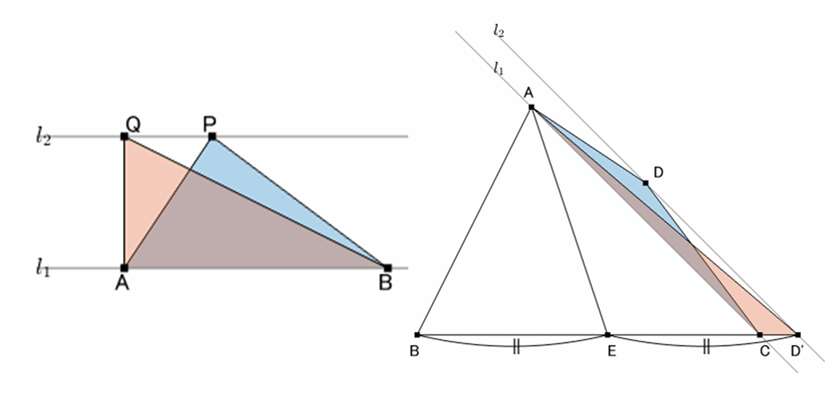
すなわち、底辺 $\mathrm{AB}$ (直線 $l_1$) に対して平行な線 $l_2$ 上を点 $\mathrm{Q}$ が動く限り、青の面積と赤の面積は (両者の高さが同じなので) 同じです。

斜めでも平行線
このように平行線が斜めになっていても等積変形を見抜けるようになりましょう。
青の面積と赤の面積は等しく、
$$\triangle\mathrm{ACD}=\triangle\mathrm{ACD^\prime}$$
です。

面積半分問題とは
面積半分問題とは、文字通り面積を半分にすることを題材にした問題ですが、高校入試の文脈では、その基本は三角形の面積を半分にすることであり、下記のようです。

すなわち、線分 $\mathrm{AE}$ は $\triangle\mathrm{ABC}$ の面積を半分に分けています。
このことを応用して、四角形の面積を半分にしたり、あるいは半分ではないような分割を求められたりしますが、基本はこの考え方です。
次の章でこれらの基本を少し応用した使い方を見てみます。
等積変形と面積半分問題の組み合わせ
問題
点 $\mathrm{A}$ を通り、四角形 $\mathrm{ABCD}$ の面積を半分にする点 $\mathrm{E}$ を作図せよ。

一気通貫アニメーション
解説
斜めでも平行線でみたように等積変形します。
このように点 $\mathrm{D^\prime}$ を取ることにより、
四角形 $\mathrm{ABCD}$ の面積 $=$ $\triangle\mathrm{ABD^\prime}$ の面積
です。

$\triangle\mathrm{ABD^\prime}$ の面積を半分にするように点 $\mathrm{E}$ を求めます。

$\triangle\mathrm{ABD^\prime}$ の面積 $=$ 四角形 $\mathrm{ABCD}$ の面積
なので、点 $\mathrm{E}$ が求める点です。
まとめ
等積変形と面積半分問題の基礎についてみてきました。
等積変形は、三角形の頂点を底辺と平行な線上で動かすことにより実現します。
また面積半分は、三角形の頂点から底辺の中点に向かって分割することにより実現します。
今回はここまでであり、基礎の部分です。次の記事↓で応用問題を扱いますので、そちらも見てください。


コメント