二次関数に面積が絡む問題は、入試でとてもよく出ます。しかし、実際に問われるパターンはそれほど多くありません。
この記事では、特に重要な5つの頻出パターンを、アニメーションで“動き”として理解できるようにまとめました。
まずは前提となるパターン0を確実に押さえ、そのうえでパターン1〜5に進むと、二次関数の面積問題が一気に得意になります。
この記事の後は、難関校の良問を集めたこちら↓にも挑戦してみてください。ここで扱う5つのパターンが、実際の入試でどのように使われているかがよく分かります。

パターン0. すべての始まりはここから
当たり前に解ける人はここを飛ばしてパターン1から始めてよいです。
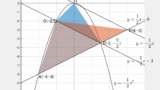
(1) 点 $\mathrm{A}$, $\mathrm{B}$ の座標を求めよ。
(2) $\triangle\mathrm{OAB}$ の面積を求めよ。

イメージ
(1) 点 $\mathrm{A}$, $\mathrm{B}$ の座標を求めよ
解
2つのグラフの交点を求めます。
\[ \begin{cases} y = x^2 \\ y = x+2 \end{cases} \]
これを連立して、
\[ x^2 = x+2 \\x^2 – x – 2 = 0 \\(x-2)(x+1)=0 \]
\[ \therefore\; x=-1,\;2 \]
\[ \mathrm{A}(-1,1),\quad \mathrm{B}(2,4) \]

(2) $\triangle\mathrm{OAB}$ の面積を求めよ
解
\[ \triangle\mathrm{OAB} = 2 \times (1+2) \times \frac12 = 3 \]

解説
$\triangle\mathrm{OAB}$ を、点 $\mathrm{C}(0,2)$ を使って2つに分けて考えます。
$\triangle\mathrm{OAB}$ $=$ $\triangle\mathrm{OAC}$ $+$ $\triangle\mathrm{OBC}$
$\mathrm{C}$ の座標が $(0,2)$ なので、$\mathrm{OC} = 2$。
$\triangle\mathrm{OAC}$ $= 2 \times 1 \times \displaystyle\frac12$
$\triangle\mathrm{OBC}$ $= 2 \times 2 \times \displaystyle\frac12$

よって、
\[ \triangle\mathrm{OAB} = 2 \times (1+2) \times \frac12 \]
この式の意味は、↓の図を見るとよく分かります。

パターン1. 等積変形
$\triangle\mathrm{OAB}$ と同じ面積になる、$y = x^2$ 上の点 の座標は?(底辺 $\mathrm{AB}$ はそのまま)

三角形の面積は 高さが同じなら面積は同じです。頂点を通り、底辺 AB に平行な直線を引けば、その直線上を動く限り高さは変わりません。
イメージ
解. 頂点に平行線を引く
求める点は、$y=x^2$ と、底辺 $\mathrm{AB}$ に平行な直線(傾き $1$)の交点です。 具体的には、$y=x$(#1)と $y=x+4$(#2)との交点を求めます。
#1. $y = x$ との交点 $\mathrm{P}$
\[ \begin{cases} y = x^2 \\ y = x \end{cases} \]
\[ x^2 = x \\ x(x-1)=0 \\ x=0,1 \]
原点 $\mathrm{O}$ は除くので、
\[ \mathrm{P}(1,1) \]

#2. $y = x + 4$ との交点 $\mathrm{Q}$, $\mathrm{R}$
\[ \begin{cases} y = x^2 \\ y = x+4 \end{cases} \]
\[ x^2 = x+4\\x^2 – x – 4 = 0 \\ x = \frac{1 \pm \sqrt{17}}{2} \]
\[ \mathrm{Q}\left(\frac{1-\sqrt{17}}{2},\; \frac{9-\sqrt{17}}{2}\right)\\ \mathrm{R}\left(\frac{1+\sqrt{17}}{2},\; \frac{9+\sqrt{17}}{2}\right) \]

解説. 底辺と平行に動く限り、面積は変わらない
言われれば当たり前ですが、この発想は入試で非常によく使います。基礎はこちら↓でしっかり身につきます。
また、求めにくい面積を求めやすくする ためにも使える重要な考え方です。下記の記事の 問題2 や 問題3 でも同じアイデアが登場します。
裏側も忘れないように
裏側とは、傾きが同じで切片が上にずれた直線のことです。今回の例では、$y=x$ と $y=x+2$ の切片の差が 2 なので、逆に 2 だけ上に移動した $y=x+4$ が裏側になります。

パターン2. 面積は高さに比例
$\triangle\mathrm{OAB}$ の面積が半分になる、$y=x^2$ 上の $\mathrm{AOB}$ 側の点の座標は?(底辺 $\mathrm{AB}$ はそのまま)

底辺 $\mathrm{AB}$ が同じなら、面積が半分ということは高さが半分ということです。頂点 $\mathrm{O}$ を通り、底辺 $\mathrm{AB}$ に平行な線に対して、そのちょうど真ん中に平行線を引けば高さが半分になります。
今回は「$\mathrm{AOB}$ 側の点」と指定されているので、裏側(反対側)は考えなくてよいです。
イメージ
解. 高さの真ん中に平行線を引く
求める点は、$y=x^2$ と、
底辺 $\mathrm{AB}$ に平行で高さが半分になる直線 $y=x+1$ との交点です。
\[ \begin{cases} y = x^2 \\ y = x+1 \end{cases} \]
より $x$, $y$ を求めて、
\[ \mathrm{Q}\left(\frac{1-\sqrt{5}}{2},\; \frac{3-\sqrt{5}}{2}\right)\\ \mathrm{R}\left(\frac{1+\sqrt{5}}{2},\; \frac{3+\sqrt{5}}{2}\right) \]

下記の問題2などがよい例です。

パターン3. 非頂点からの面積半分問題(定点編:等積変形)
点 $\mathrm{C}(0,2)$ を通り、$\triangle\mathrm{OAB}$ の面積を二等分する直線は?

イメージ
解. 等積変形をうまく使う
まず、$\mathrm{OB}$ の中点 $\mathrm{M}$ をとります。 $\mathrm{B}(2,4)$ なので、
\[ \mathrm{M}(1,2) \]
このとき、
$\triangle\mathrm{MAB}$ は $\triangle\mathrm{OAB}$ の半分
になります。

次に、点 $\mathrm{A}$ を通り $\mathrm{CM}$ に平行な直線を引き、$\mathrm{OB}$ との交点を $\mathrm{P}$ とします。
$\triangle\mathrm{ACM}$ と $\triangle\mathrm{PCM}$ の面積が等しい
ため、
$\triangle\mathrm{PCB}$ の面積が $\triangle\mathrm{OAB}$ の半分

よって、求める直線は $\mathrm{CP}$ の式です。
\[ y = -2x + 2 \]

この解法は、下記の記事で詳しく解説しています。
別解もあります。下記記事で紹介。
パターン4. 非頂点からの面積半分問題(平行線編:パラメータ)
$x$ 軸と平行で、$\triangle\mathrm{OAB}$ の面積を二等分する直線は?

イメージ
解. 強引に解くしかない
この問題は、パターン3のような美しい等積変形が使えません。 ただし、イメージアニメーションの通り、直線が決まれば面積も決まるという事実を使って、式を立てていきます。
解
まず、試しに $y=1$ と $\mathrm{OB}$ の交点を $\mathrm{P}$ とします。
図より明らかに $\triangle\mathrm{OAP}<\triangle\mathrm{BAP}$ なので、
面積を半分にする直線 $y=k$ は、
\[1<k<4\tag{4-1}\label{eq4-1}\]
の範囲です。
このとき、直線 $y=k$ と $\mathrm{AB}$, $\mathrm{OB}$ の交点 $\mathrm{Q}$, $\mathrm{R}$ は、
\[ \mathrm{Q}(k-2,\; k),\qquad \mathrm{R}\left(\frac{k}{2},\; k\right) \]

$\triangle\mathrm{BQR}$ の面積は、
\begin{eqnarray}
\triangle{\mathrm{BQR}} &=& \left\{\frac{k}{2} – (k-2)\right\} \times (4-k) \times \frac12\\
&=& \left(2 – \frac{k}{2}\right)(4-k)\frac12\\
&=& \frac14 (4-k)^2
\end{eqnarray}
これが $\triangle\mathrm{OAB}$ の半分(= $\displaystyle\frac32$)になればよいので、
\[ \frac14 (4-k)^2 = \frac32 \\ (4-k)^2 = 6 \\ 4-k = \pm\sqrt{6} \]
ただし、$k<4\;(\because\eqref{eq4-1})$ なので、
\[ k = 4 – \sqrt{6} \]
よって、求める直線は、
\[ y = 4 – \sqrt{6} \]
解説1. 計算は工夫しよう(展開しない)
展開しても解けますが、展開しない方が圧倒的に楽です。 細かい工夫ですが、計算の速さと正確性に大きく影響します。
解説2. +の方はどうなる?
$k = 4+\sqrt{6}$ を選ぶと、直線が $\mathrm{B}$ より上側に来てしまい、 $\triangle\mathrm{OAB}$ を二等分することはできません。

この不適切な解を排除するために、最初に $1< k< 4$ \eqref{eq4-1} と範囲を絞ったわけです。
パターン5. 台形の分割
二次関数とは直接関係しませんが、パターン0の設定から誘導されてこのタイプの問題に発展することがあります。入試ではよく見かける流れなので、ここで扱うパターンに含めました。
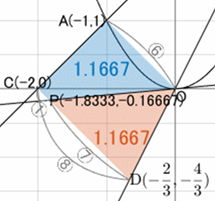
原点 $\mathrm{O}$ を通り、台形 $\mathrm{OACD}$ を二等分する直線 $\mathrm{OP}$ の式は?

イメージ
台形は「高さが一定」という特徴があります。したがって、面積を二等分するには、底辺の比がそのまま面積比になります。アニメーションでは、直線を動かすと面積がどう変わるかが視覚的に分かります。
実際の入試では点 $\mathrm{D}$ を求めさせることが多いですが、この記事では本質ではないため省略します。
解. 底辺比 = 面積比
解
\[ \mathrm{OA} : \mathrm{CD} = 6 : 8 \]
(理由は後述「解説1」)
台形 $\mathrm{OACD}$ を二等分するには、
底辺 $\mathrm{CD}$ を$1:7$ に分ける点 $\mathrm{P}$
をとればよい(理由は後述「解説2」)。
よって、
\[ \mathrm{P}\left(-\frac{11}{6},\; -\frac{1}{6}\right) \]
原点 $\mathrm{O}$ と $\mathrm{P}$ を結ぶ直線 $\mathrm{OP}$ の式は、
\[ y = \frac{1}{11}x \]
解説1. $\mathrm{OA} :\mathrm{CD} = 6 : 8$ になる理由
$\mathrm{A}$ と $\mathrm{D}$ の $y$ 座標 (の大きさ) を見比べています。
$\mathrm{A}$ の $y$ 座標 $1$ : $\mathrm{D}$ の $y$ 座標 $\displaystyle\frac43 = 6:8$

台形なので $\mathrm{OA}/\! /\mathrm{CD}$ です。平行な2辺を持つ図形では、長さの比 = $x$座標(または $y$座標)の差の比になります。
解説2. なぜ $\mathrm{CD}$ を $1 : 7$ に分けるのか
高さが一定なので、面積比は底辺の比に一致します。台形の方は「上底+下底」です。$\mathrm{CD}$ を $1 : 7$ に分けることで、
青の「上底+下底」の長さ $=⑥+①=⑦$
赤の「底辺」の長さ $=⑧-①=⑦$
と、等しくなります。

解説3. $\mathrm{P}$ の座標の求め方
$\mathrm{CD}$ を $1 : 7$ に分ける点の座標は、内分点の公式で求められます。
\[ \mathrm{P} = \frac{7\mathrm{C} + 1\mathrm{D}}{7 + 1} \]

計算すると、 \[ \mathrm{P}\left(-\frac{11}{6},\; -\frac{1}{6}\right) \] となります。
まとめ. 二次関数の面積は「パターン」で攻略する
二次関数の面積問題は、一見すると複雑ですが、実際には決まったパターンの組み合わせで構成されています。この記事で扱ったパターン0〜5を押さえておけば、入試で出てくる多くの問題に対応できます。
- パターン0:基本設定(交点・面積の基礎)
- パターン1:等積変形(高さ一定)
- パターン2:高さが半分 → 面積も半分
- パターン3:非頂点からの二等分(定点:等積変形)
- パターン4:非頂点からの二等分(平行線:パラメータ)
- パターン5:台形の分割(底辺比 = 面積比)
特に、パターン1・2・3は入試での出題頻度が高く、ここを確実に理解しておくと得点力が大きく伸びます。
次のステップとして、実際の入試問題でこれらのパターンがどのように使われているかを確認してみてください。理解が一段深まり、応用力が身につきます。




コメント