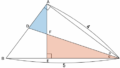
蝶々型の相似は頻出です。サムネ画像(問題1)のように蝶々型が表に現れているものは難なく解けるようにしたいところです。その上で、問題2や3のように蝶々型が隠れている場合もしっかりと見抜けるようにしましょう。
この次は入試問題↓にも挑戦してください。
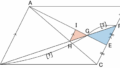
問題設定1 初級:蝶々型の基本形
問題
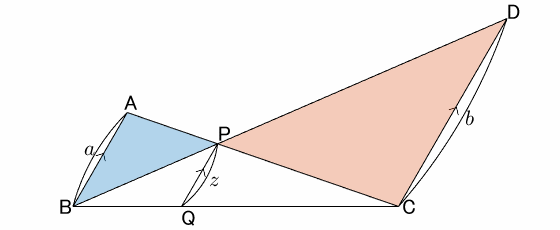
x, y, z を求めよ。

蝶々型は特徴的な形なので蝶々型であることはすぐに分かると思います。その中に相似が3つ隠されています。
△PAB∽△PCD△CAB∽△CPQ△BDC∽△BPQ
それらを全部もしくはいくつか使って値を出します。
イメージ
解
△PAB∽△PCD, AB:CD=1:2 より、
AP:PC=1:2

ゆえに、
x+y=9x:y=1:2
∴x=3,y=6
さらに、△CPQ∽△CAB より、
CP:CA=2:3=z:3
∴z=2

解説
1. 覚える必要はないが、美しい関係式がある
z=2 を求める際、美しい関係式があります。答えを先に示すと、
z=積和
です。つまり、
z=3×63+6=189=2
です。少し深堀します。3 の部分を a と置き、6 の部分を b と置きます。
まず、△ABC∽△PQC より、
za=QCBC
同様に、△DCB∽△PQB より、
zb=BQBC
(1)+(2)より、
za+zb=QCBC+BQBC=BCBC=1
両辺を z で割ると、
1a+1b=1z
これを z について解くと、
z=aba+b
この z を
a, b の調和平均
と言います。これに対して通常求めるような、総和を個数で割って求める平均は「算術平均」と言います。
問題設定2 初中級:蝶々型の応用形
問題
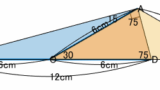
x, y, z を求めよ。四角形ABCDは平行四辺形である。

見た目に騙されないように
この図形は MB=3 に気づけば「問題設定1」と全く同じです。
解
MB=3 以下、「問題設定1」と同じより、
x=3,y=6,z=2
問題設定3 中級:補助線入れたらすぐ解ける
問題
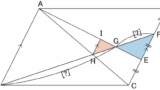
?を求めよ。

イメージ
解
AD を線で結ぶと、
△ADE∽△GFE
であり、
相似比は 3:1

ゆえに、
FG=6×13=2

別解
補助線が思いつかなかった場合でも「問題設定1」に倣って解くことができます。
FG を求めたいですが、一気には難しそうなので、FI=x, IG=y と分割して置くことにします。
そうすると、
EI:AB=1:4
EI:DC=1:4
より下図が書けます。

そうすると、
3x+3y=6
なので、
x+y=2
となり、これは求めたかった FG そのものなので、これが答えとなります。
まとめ
蝶々型の図形から相似を発見するパターンを見てきました。隠れ蝶々型も見ました。図形の問題を苦手にする人が多いですが、隠れ図形が楽に見抜けるようになれば楽しくなります。
このシリーズでは平面図形の問題に出会った際、教科書的な求め方はもちろん、それ以外の求め方にも触れることで発想法の引き出しを増やします。引き出しが増えれば問題を見た際に、さてどれで解こうかな、とパズル的な楽しみが出てきます。また、それら解法が点と点でつながり、さらに強固なイメージへとつながります。シリーズ最初はこちら↓です。

コメント