直角三角形の三辺が既知で高さを求める際、大抵の人は相似を使いますが、面積を活用することで一瞬で求められます。さらに、他の点から高さの足までの長さは円を発想することで相似を考えることなく楽に求められます。
この記事を読み終えた後はこちらの記事↓にも挑戦ください。
このシリーズでは平面図形の問題に出会った際、教科書的な求め方はもちろん、それ以外の求め方にも触れることで発想法の引き出しを増やします。引き出しが増えれば問題を見た際に、さてどれで解こうかな、とパズル的な楽しみが出てきます。また、それら解法が点と点でつながり、さらに強固なイメージへとつながります。
シリーズ最初はこちら↓です。
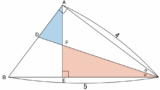
問題設定:直角頂点から下ろした垂線の足でできる3線分の長さを求める
$x$, $y$, $z$ を求めよ。

$x$ を求める

解1(初級). 相似:ほとんどの人はこれで解く
この問題を見たらほとんどの人はこの解法で解くと思います。それは、相似を学習する際に代表的な問題として出てくるからです。実際には次の解2に示す面積の解法の方がシンプルで楽です。
しかし、解法の引き出しとして直角三角形を見たら常に相似を意識することは大切です。
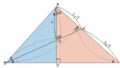
相似のイメージ

解
$\triangle\mathrm{ABC}\unicode[sans-serif]{x223D}\triangle\mathrm{HAC}$ より、
\begin{eqnarray}
3:x &=& 5:4\\
3\times 4 &=& 5x\\
\therefore\; x &=& \frac{12}{5}
\end{eqnarray}
解2(上級). スマートな解法_面積:楽に求められ、空間図形にも応用が利く
こちらの解法で解く人はなかなかセンスが良いなと思います。解1の相似の解法よりもずっと楽に解けるからです。
ただし、この解法で三角形の高さを求められるのは、$\triangle\mathrm{ABC}$ が直角三角形であるときに限ります。
これは、$\triangle\mathrm{ABC}$ の面積を底辺の見方を変えて2通りの方法で表します。三角形の面積の計算には常に係数 $\displaystyle\frac{1}{2}$ がついてくるので、ちょっとしたテクニックとしては三角形の2倍の面積 $2\triangle\mathrm{ABC}$ を持ち出すとすっきりします。
解
三角形の面積を2通りの方法で表す。すなわち、
\begin{eqnarray}
2\triangle\mathrm{ABC} &=& 3\times 4\\
&=& 5x\\
\therefore\; x &=& \frac{12}{5}
\end{eqnarray}
解説
解1と2は結局同じ
解1と解2は結局同じ式であることに注目しましょう。全く同じ式なので考えやすい方で考えればよいです。そうなると、解2の方が考えやすいですね。相似図形を考える手間が無いので。
解2は空間図形でもよく使うテクニック
解2の解法は空間図形でもよく使います。「三角錐の頂点から底面に下した垂線の足の長さを求めよ」というもので、体積と底面積が容易に求められる場合に使います。
例えばこちらの記事↓の問題3(2)です。
実際には三辺の内の一つは隠されている
実際の問題では $\triangle\mathrm{ABC}$ の三辺の内のどれか一つは隠されている状態で出題されます。直角三角形という条件から三平方の定理を用いて残りの一辺を求めさせてから始める感じになります。
三平方の定理は中三で習うため、ここでは未学習者も見る可能性を考慮して三辺を予め示しました。
あるいは、より本質的には「$x$, $y$, $z$ のような部分を求める求め方」に注力してもらいたいため、その他の部分は予め示したという側面もあります。
三平方の定理についてはこちら↓に分かりやすい証明アニメーションを作りました。
$y$ を求める

解1(初級). 相似:ほとんどの人はこれで解く
$x$ を求めた際と同様ですが、直角三角形を見たら相似を意識することは基本としておきましょう。
相似のイメージ

解
$\triangle\mathrm{ABC}\unicode[sans-serif]{x223D}\triangle\mathrm{HBA}$ より、
\begin{eqnarray}
3:y &=& 5:3\\
5y &=& 3^2\\
\therefore\; y &=& \frac{9}{5}
\end{eqnarray}
解2(上級). スマートな解法_方べきの定理:円とのコラボ
$\triangle\mathrm{AHC}$ は直角三角形です。そこに円が見えれば方べきの定理が使えます。方べきの定理は中三の円の単元で習います。
方べきの定理のイメージ

解
方べきの定理より、
\begin{eqnarray}
5y &=& 3^2\\
\therefore\; y &=& \frac{9}{5}
\end{eqnarray}
解説
解1と2は結局同じ
解1と解2は結局同じ式であることに注目しましょう。全く同じ式なので考えやすい方で考えればよいです。方べきの定理は中三で習うところなので少し高度ではありますが、こちらで慣れておくと円の問題でも発想が湧いてくるようになるのでおススメです。
なお、方べきの定理の証明は三角形の相似を用いてなされるため、本質的に解1と解2は同じです。
円とのコラボといえば・・・
円とのコラボといえばこちらも面白い発想です。円とのコラボつながりで理解を深めればより効果的ですので、見てみてください。
$z$ を求める

解1. 相似
直角三角形を見たら常に相似を意識しましょう。
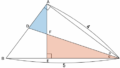
相似のイメージ

解
$\triangle\mathrm{ABC}\unicode[sans-serif]{x223D}\triangle\mathrm{HAC}$ より、
\begin{eqnarray}
4:z &=& 5:4\\
5z &=& 4^2\\
\therefore\; z &=& \frac{16}{5}
\end{eqnarray}
解2. 方べきの定理
方べきの定理のイメージ

解
方べきの定理より、
\begin{eqnarray}
5z &=& 4^2\\
\therefore\; z &=& \frac{16}{5}
\end{eqnarray}
解3(素直). 引き算:$y$ が分かっているならこれで十分
$y$ が既に分かっていれば、引き算ですぐに求まります。
解
\begin{eqnarray}
z &=& 5-y\\
&=& 5-\frac{9}{5}\\
&=& \frac{16}{5}
\end{eqnarray}
$x$, $y$, $z$ を一度に求める:三平方の定理
$y$ と $z$ には $y+z=5$ という関係があるため、$z$ は予め $5-y$ としておきます。

解1(万能). $\triangle\mathrm{ABC}$ が直角三角形でなくても使える万能薬
これまでの解法(特に解2)は全て $\triangle\mathrm{ABC}$ が直角三角形のときに使えるものです。解1の相似は、直角三角形でないときにも相似の場合もありますが、任意の三角形というわけにはいきません。それに対してこの解法は $\triangle\mathrm{ABC}$ の形状は任意です。
解
$\triangle\mathrm{ABH}$ に三平方の定理を適用すると、
$$x^2+y^2=3^2\tag{1}\label{p3808eq1}$$
同様に、$\triangle\mathrm{ACH}$ に三平方の定理を適用すると、
$$x^2+(5-y)^2=4^2\tag{2}\label{p3808eq2}$$
\eqref{p3808eq2}-\eqref{p3808eq1}
\begin{eqnarray}
(5-y)^2-y^2 &=& 16-9\\
(25-10y+\cancel{y^2})-\cancel{y^2} &=& 7\\
-10y &=& 7-25\\
10y &=& 18\\
y &=& \frac{9}{5}
\end{eqnarray}
これを\eqref{p3808eq1}に代入して
\begin{eqnarray}
x^2 &=& 3^2-\left(\frac{9}{5}\right)^2\\
&=& 9\left(1-\frac{9}{25}\right)\\
&=& 9\cdot\frac{16}{25}\\
&=& \left(\frac{3\times4}{5}\right)^2\\
\therefore\; x &=& \frac{12}{5}\quad (\because x>0)\\
\therefore\; z &=& 5-y\\
&=& \frac{16}{5}
\end{eqnarray}
解説
$\triangle\mathrm{ABC}$ が直角三角形のときには解2で示したように面積や方べきの定理を用いると楽です。直角三角形でない時には三平方の定理を使って求めることになります。
まとめ
直角三角形の相似の基本部分を押さえました。それにより各種の辺の長さを求めました。その際、相似を利用するだけでなく様々な方法での解法にも触れました。いずれの解法を取るにせよ、
三角形の三辺が既知の場合は、
頂点から下した垂線の足でできる3線分の長さは分かる
と理解しましょう。
三角形がたまたま直角三角形であった場合では、おススメは、$x$ を求める際に使った面積の方法と、$y$, $z$ を求めると気に使った方べきの定理の方法です。
解法の中には中三後半で学ぶ部分もあり未学習の人もいると思いますが、その部分は今のところは読み飛ばしてもよいですし、また内容的にはそれほど難しくもないのでこの機に学習してみるのもいいと思います。
いろいろな見方ができると、それぞれで学んだ「点と点の知識」が線で結ばれて行きます。

コメント