ここでは円周角の定理の証明を、さっとイメージで理解します。
円周角の定理とは
円周角の定理とは、中心角と円周角の関係を謳ったもので、次のようです。
円周角の定理

証明
アニメーションでイメージ
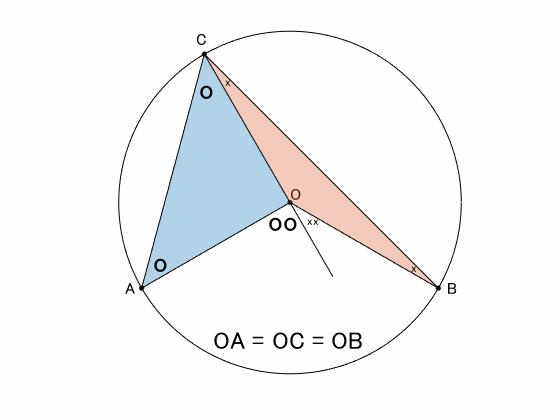
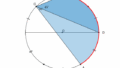
証明は、OCを結んでできる三角形が二等辺三角形であることを用います。
二等辺三角形に着目
青の三角形と赤の三角形はともに二等辺三角形です。従って青の三角形に着目すれば、
$$\angle\mathrm{OCA}=\angle\mathrm{OAC}=”\mathrm{o}”$$
であり、その外角は “oo” です。
赤の三角形にも同様のことが言えるので、角度を “x” と書くことにします。アニメーションでは “o” と “x” の角度は刻一刻と変わっていますが、同じ記号を使っています。その代わりに大きさを変えています。
さて、このように書けばもう明らかなように、
$$\angle\mathrm{ACB}=”\mathrm{ox}”$$
であるのに対し、
$$\angle\mathrm{AOB}=”\mathrm{ooxx}”$$
です。
これで証明のイメージは終わりです。
点Cは円上を移動しても角度は変わらない
点 $\mathrm{C}$ が円上を動いても(同じ側の弧であるとする)、$\angle\mathrm{AOB}$ は変わりません。なぜなら、動いているのは $\mathrm{C}$ だけであって、$\mathrm{A}$ も $\mathrm{O}$ も $\mathrm{B}$ も動いていないからです。

そして “o” と “x” の大きさ自体は異なりますが、”o” と “x” の関係は変わらないので、円周角は中心角の半分であり続けます。
本当はこのようなケースも考えないといけない
厳密には点 $\mathrm{C}$ がさらに移動した下記のようなケースも考えないといけないですが、ここではイメージを持つことを目的にするため、省略します。

特別な場合:直角三角形
直径の円周角と見る
円周角の定理の特別な場合として、直径の円周角がたびたび取り上げられます。直径の中心角は $180^\circ$ なので、その円周角は $90^\circ$ です。つまり、直角三角形です。

外接円の直径と見る
上記の逆の見方ですが、応用力を試す問題として下記のようなものがあります。
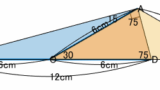
?の角度を求めよ。

これのミソは三角形 $\mathrm{ABD}$ が直角三角形であり、上記のように外接円が見えることです。これの解答は下記↓の記事にあります。
まとめ
円周角の定理の証明の本質的な部分をイメージで理解しました。補助線 $\mathrm{OC}$ を入れることにより $\mathrm{OA}=\mathrm{OC}=\mathrm{OB}$ から二等辺三角形が二つ見え、それゆえに外角の定理を使うことにより円周角の定理が証明できます。
ただ一方で円周角の定理そのものの証明が入試等で出ることはまれで、大抵は弧長を用いた角度の計算問題です。下記↓の記事で取り上げました。

コメント