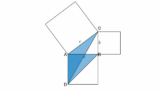
三角定規の辺の比は基本の直角三角形です。三角定規を2つ合わせてできる三角形が見落としがちな三角形です。105度とか75度とかが出てきますが、この角度をみてピンとくるようにしておきたいものです。また、5-12-13と3-4-5の直角三角形の組み合わせも、面白い形をしています。
三平方の定理そのものの理解は、鮮やかな証明を下記で行っているので、そちらを参照ください。
基本の直角三角形
まずは基本形から確認していきます。

上の二つは三辺の比が整数になる組み合わせです。
下の二つは三角定規です。
どちらも頻出なので、これは基本形として確実に覚えておきましょう。
特殊な直角三角形1
105度編
問題にしてみる
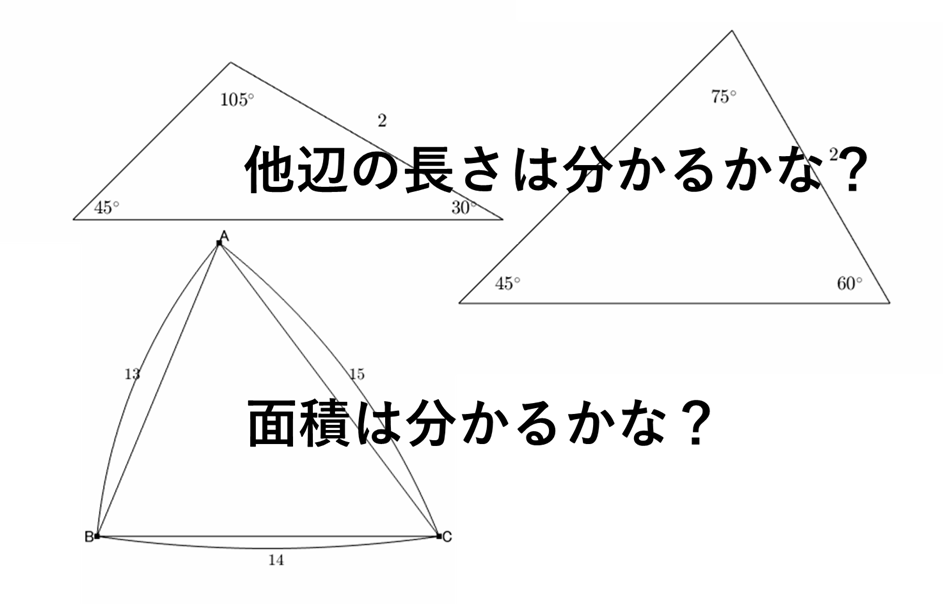
下の三角形の残りの辺の長さを求めよ。

三角定規をくっつけた三角形
一気通貫アニメーションで確認します。
くっつける様をアニメーションで確認
75度編
問題風にしてみる
下の三角形の残りの辺の長さを求めよ。

三角定規をくっつけた三角形
一気通貫アニメーションで確認します。
くっつける様子をアニメーションで確認
特殊な直角三角形2
三辺の長さ編
問題風にしてみる
面積を求めよ。

面積を求めるには高さが欲しいです。
基本の直角三角形をくっつけた三角形
一気通貫アニメーションで確認します。
解答が書けるように
まずは点 $\mathrm{A}$ から辺 $\mathrm{BC}$ に垂線を下ろします。

直角三角形が二つできますので、底辺の長さを文字で置きます。$\mathrm{BH}=x$ と置けば、$\mathrm{HC}=14-x$ です。

ここで、二つの直角三角形それぞれに三平方の定理を適用します。まずは左側。

そして、右側。

二つの式が $\mathrm{AH}^2$ で結ばれているので、$x$ について解きます。
計算は省略して、$x=5$ と求まります。

すると、$\mathrm{BH}=5$, $\mathrm{HC}=9$ と求まります。
$x=5$ が求まれば、これを $\mathrm{AH}$ の式に代入することにより、
$$\mathrm{AH}=12$$
もすぐに求まります。

これは、よく見ると基本の直角三角形を二つくっつけたものになっています。
問題は、面積を求めよ、でしたので、求めます。

まとめ
見落としがちな特殊な三角形を取り上げました。結構高校入試で頻繁に出てきますが、発想の引き出しを持っていないとなかなか思いつきません。
$$45^\circ+60^\circ=105^\circ$$
$$45^\circ+30^\circ=75^\circ$$
の角度を見たらピンとくるように引き出しにしっかりとしまっておきましょう。


コメント