食塩水の濃度問題は、中学数学でもつまずきやすい単元の一つです。「混ぜる」「薄める」「蒸発させる」などパターンが多く、公式だけ覚えても応用が効かないと感じる人は少なくありません。この記事では、どんな問題でも迷わず解けるようになる “食塩の量に着目する解法” を、図を使って体系的に整理しました。混合・加水・蒸発・加塩など、入試で頻出のパターンをすべてカバーしています。食塩水問題を根本から理解したい人は、ぜひ読み進めてください。
基本の計算を確認
濃度の計算
濃度は次の式で求めます。

例えば、$200\mathrm{g}$ の食塩水の中に食塩が $12\mathrm{g}$ 溶けているなら、
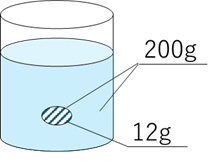
$$\frac{12}{200}=\frac{6}{100}=0.06$$
$0.06$ が濃度です。これを $\%$ に直すと、$6\%$ です。
公式よりも意味の理解を
濃度を求める公式は上で示したように、

ですが、これはつまり、
食塩水 $1\mathrm{g}$ の中に入っている食塩の重さ
を表しています。食塩水の重さで割るということは、食塩水 $1\mathrm{g}$ 当たりを求めている、ということです。割り算が $1$ 当たりを求めているということについては下記の記事↓で面白い見方含めてじっくりと取り組んでいます。
また、この $1$ 当たりに $100$ を掛けると当然 $100$ 当たりを求めていることになりますが、これがいわゆる $\%$ です。つまり、
$6\%$ というのは、食塩水 $100\mathrm{g}$ 当たりに食塩が $6\mathrm{g}$ 入っている濃度
ということです。
図を描きましょう
ここで強調したいのは、図を描きましょうということです。図を描くことで食塩量の変化や水量の変化が同時に、しかも直感的に分かるためです。特に、食塩水問題の本質は「食塩量保存」であり、これが一目で理解できることが大きいです。
図を描きながら問題を解くことを通じて、直感的にわかる感覚を会得していくことで、どんな問題でも解けるという自信につながります。
自分で図を描くときにはきれいな図は不要です。こんな感じで充分です。
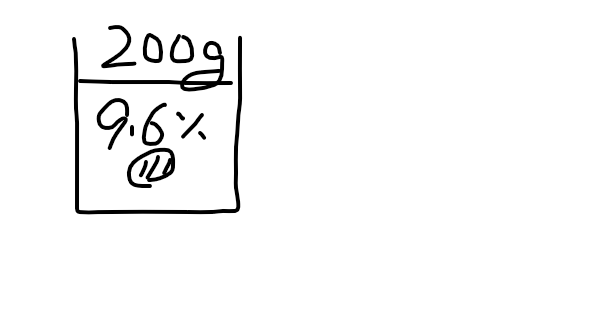
食塩の重さの計算
上記の公式を式変形しただけです。

実際の問題ではこちらをよく用います。例えば、$6\%$ の食塩水 $200\mathrm{g}$ に含まれる食塩の重さは、
$$200\times 0.06=12 \mathrm{[g]}$$
です。
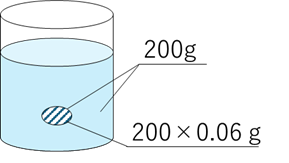
「の」は×(掛ける)
ここで面白いテクニックを教えます。「のは×(掛ける)」です。
例えば上記の例を再掲して、「$6\%$ の食塩水 $200\mathrm{g}$」なら、
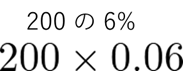
という具合です。ほかの例も見てみましょう。
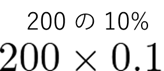
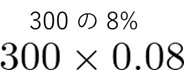
という具合です。簡単でしょう? これが食塩の重さです。
混合(混ぜる)
ここからは実際の問題をパターン別に見ていきます。水の量と食塩の量に着目するのがポイントです。その際、必ず図を描くようにしましょう。
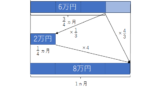
$ 8\%$ の食塩水 $ 300\mathrm{g}$ と、$ 12\%$ の食塩水 $ 200\mathrm{g}$ を混ぜる
$ 8\%$ の食塩水 $ 300\mathrm{g}$ と、$ 12\%$ の食塩水 $ 200\mathrm{g}$ を混ぜると、何 $\%$ の食塩水になるか?
図を描きましょう。
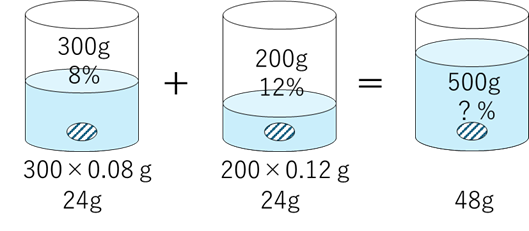
よって濃度は、
$$\frac{48}{500}=0.096$$
$$9.6\%$$
$ 0.096$ の出し方のちょっとしたコツ
もちろん下記のように素直に割り算をすればよいです。
\begin{eqnarray}
\require{enclose}
0.096 \\
500 \enclose{longdiv}{48} \phantom{000} \\
\underline{4500} \phantom{0} \\
3000 \\
\underline{3000} \\
0
\end{eqnarray}
しかしここでちょっと工夫をして、$48$ に $2$ を掛けるという発想を持つと楽です。実際、
$$48\times 2=96$$
なので、答えにぐっと近づいていますよね。そして、$48$ である分子に $2$ を掛けている訳なので同じように分母である $500$ にも $2$ を掛けます。そうすると、$1000$ です。ここから、$0.096$ が導けます。これはつまり、次の計算をしていることになります。
$$\frac{48}{500}=\frac{96}{1000}=0.096$$
このような計算の工夫ができると、楽でミスがありません。
加水
$ 10\%$ の食塩水 $ 150\mathrm{g}$ に水 $ 50\mathrm{g}$ を加える
まず、水で薄めているので元の $10\%$ よりは薄くなるな、という感覚を持ちましょう。この感覚が意外と計算ミスを防ぎます。
$10\%$ の食塩水 $150\mathrm{g}$ に水 $50\mathrm{g}$ を加えた。新しい濃度は何 $\%$ か?
図を描きましょう。
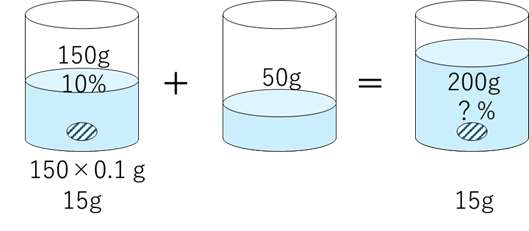
よって濃度は、
$$\frac{15}{200}=0.075$$
$$7.5\%$$
$ 7.5\%$ の出し方のちょっとしたコツ
この場合は、$15$ を $2$ で割るだけで $\%$ が出ます。なぜなら、$\%$ とは $100\mathrm{g}$ 当たりなので。あえて式で表すと下記です。
$$\frac{15}{200}=\frac{7.5}{100}$$
蒸発
$ 10\%$ の食塩水 $ 150\mathrm{g}$ から水 $ 50\mathrm{g}$ を蒸発させる
この場合は、水を蒸発させているので濃度は増します。
$10\%$ の食塩水 $150\mathrm{g}$ から水 $50\mathrm{g}$ を蒸発させた。新しい濃度は何 $\%$ か?
図を描きましょう。
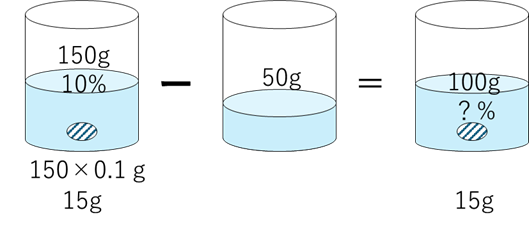
よって濃度は、
$$\frac{15}{100}=0.15$$
$$15\%$$
加塩
$ 4\%$ の食塩水 $ 600\mathrm{g}$ に $ 40\mathrm{g}$ の食塩を加える
この場合は、塩を加えているので濃度は増します。
$4\%$ の食塩水 $600\mathrm{g}$ に $40\mathrm{g}$ の食塩を加えた。新しい濃度は何 $\%$ か?
図を描きましょう。
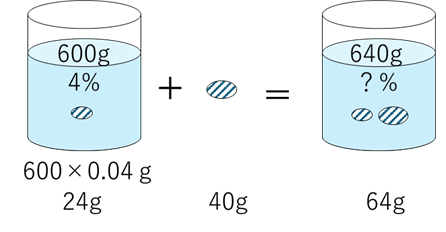
よって濃度は、
$$\frac{64}{640}=\frac{10}{100}=0.1$$
$$10\%$$
複合:食塩水を捨てて水を加える
濃度 $ 10\%$ の食塩水 $ 300\mathrm{g}$ がある。このうち $ 60\mathrm{g}$ を捨てて、同じ量の水を加えた。
この場合は、結局塩分だけ抜けているので濃度は下がります。
濃度 $10\%$ の食塩水 $300\mathrm{g}$ がある。このうち $60\mathrm{g}$ を捨てて、同じ量の水を加えた。新しい濃度は何 $\%$ か?
図を描きましょう。
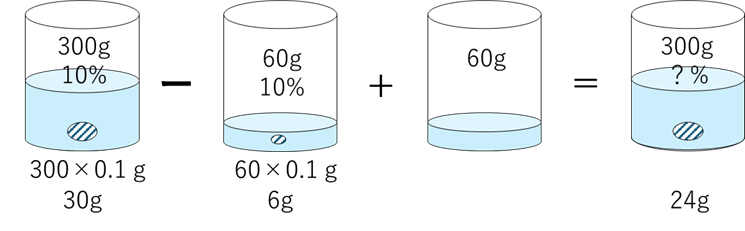
よって濃度は、
$$\frac{24}{300}=\frac{8}{100}=0.08$$
$$8\%$$
指定濃度
この場合は方程式になります。
$ 4\%$ の食塩水 $ 600\mathrm{g}$ に 食塩を加えて $ 10\%$ にする
$4\%$ の食塩水 $600\mathrm{g}$ に食塩を加えて $10\%$ の食塩水を作りたい。加える食塩は何 $\mathrm{g}$ か?
図を描きましょう。
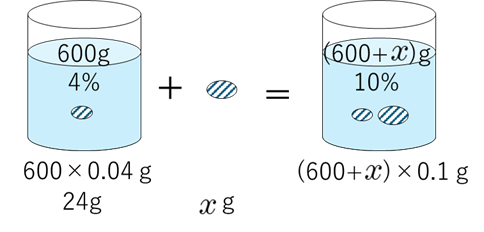
よって、次の方程式が成り立つ。
$$24+x=(600+x)\times 0.1$$
$x$ を解いて、
$$x=40$$
$$40\mathrm{g}$$
これは、加塩の方程式版です。
$ 8\%$ の食塩水 $ 300\mathrm{g}$ と $ 12\%$ の食塩水を混ぜて $ 9.6\%$ の食塩水を作る
$8\%$ の食塩水と $12\%$ の食塩水を混ぜて $9.6\%$ の食塩水を作りたい。$8\%$ の食塩水を $300\mathrm{g}$ 使うとき、$12\%$ の食塩水は何 $\mathrm{g}$ 必要か?
図を描きましょう。
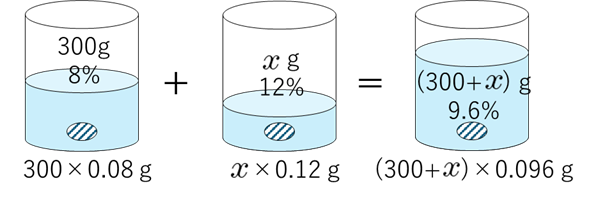
よって、次の方程式が成り立つ。
$$300\times 0.08+x\times 0.12=(300+x)\times 0.096$$
$x$を解いて、
$$x=200$$
$$200\mathrm{g}$$
これは、混合の方程式版です。
$ 8\%$ の食塩水と $ 12\%$ の食塩水を混ぜて $ 9.6\%$ の食塩水を $ 500\mathrm{g}$ 作る
$8\%$ の食塩水と $12\%$ の食塩水を混ぜて $9.6\%$ の食塩水を $500\mathrm{g}$ 作りたい。それぞれの濃度の食塩水何 $\mathrm{g}$ 必要か?
図を描きましょう。
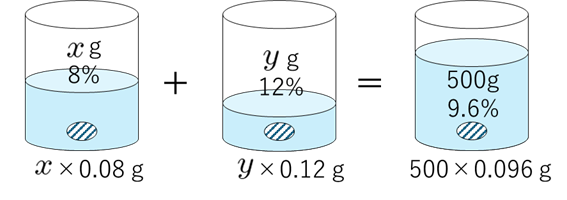
よって、次の方程式が成り立つ。
\begin{eqnarray}
x+y &=& 500\\
x\times 0.08+y\times 0.12 &=& 500\times 0.096
\end{eqnarray}
$x,\; y$ を解いて、
$$x=300,\; y=200$$
$8\%$ の食塩水 $300\mathrm{g}$、$12\%$ の食塩水 $200\mathrm{g}$
これは、混合の連立方程式版です。
まとめ
食塩水問題を網羅的に扱いました。食塩水問題を代表とする濃度や割合の問題は苦手にしている人も多いですが、コツをつかめば非常に簡単です。食塩水問題の場合は、食塩の量に着目する、です。

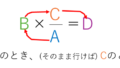

コメント