空間図形は「見えないから難しい」と感じる人が多い分野です。切断面の形や高さの位置関係がつかめないまま式だけ追ってしまうと、どこで何をしているのか分からなくなってしまいます。
この投稿では、まずアニメーションで “立体の動き” や “切断の様子” を視覚的につかみ、次に図形の構造を丁寧に整理し、最後に計算へ落とし込む流れで進めていきます。
3つの問題を通して、空間図形に共通する「見方」が自然と身につくように構成しています。イメージ → 構造 → 計算 の順で読み進めてみてください。
問題1:正四角錐の切断1(底面の角から切断)
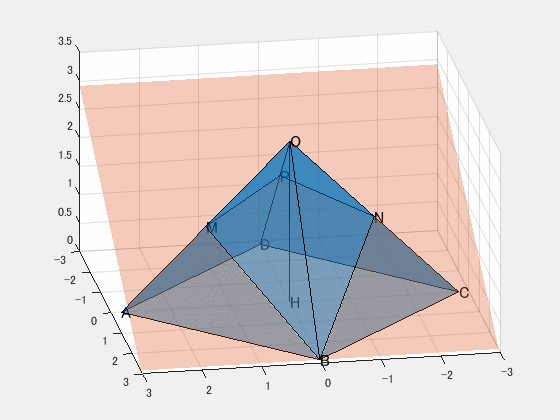
図のように、すべての辺の長さが 4cm の正四角錐 $\mathrm{O\!-\!ABCD}$ がある。辺 $\mathrm{OA}$, $\mathrm{OC}$ の中点をそれぞれ $\mathrm{M}$、$\mathrm{N}$ とする。また、点 $\mathrm{O}$ から底面 $\mathrm{ABCD}$ に垂線 $\mathrm{OH}$ を下ろす。この正四角錐を 3 点 $\mathrm{B},\mathrm{M},\mathrm{N}$ を通る平面で切ったとき、

(1) $\mathrm{OH}$ の長さを求めよ。
(2) 切り口の面積を求めよ。
(3) 2 つに分けた立体のうち、点 $\mathrm{O}$ を含む方の体積を求めよ。
(23年 東海高校)
まずは切断のイメージをつかみましょう。次のアニメーションを見ると、平面 $\mathrm{BMN}$ がどのように立体を貫いているかが分かります。
解(1). $\mathrm{OH}$ の長さ
(1) $\mathrm{OH}$ の長さを求めよ。
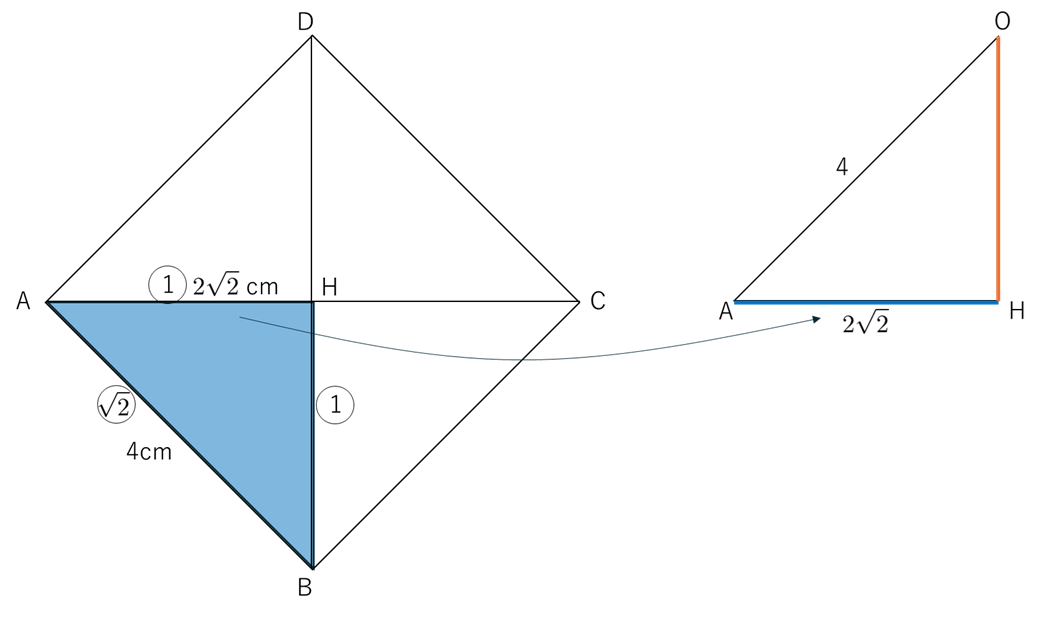
底面 $\mathrm{ABCD}$ は正方形なので、$\triangle \mathrm{AHB}$ は直角二等辺三角形です。したがって、
$\mathrm{AH}$ $= 2\sqrt{2} $
三平方の定理より、
$\mathrm{OH}^2$ $= 4^2 -$ $(2\sqrt{2})^2$ $= 8$
$\mathrm{OH}$ $= 2\sqrt{2}$
解(2). 切り口の面積
(2) 切り口の面積を求めよ。
切り口は四角形 $\mathrm{BMPN}$ です。二等辺三角形を二つ重ねた四角形です。
面積は次の式で求められます。
$$ S = \frac12 \cdot \mathrm{MN} \cdot \mathrm{BP} $$
したがって、$\mathrm{MN}$ と $\mathrm{BP}$ の 2 本の長さを求めれば十分です。

$\mathrm{MN}$ の長さ
$\mathrm{M}$ と $\mathrm{N}$ は対角線 $\mathrm{AC}$ の中点なので、
$$ \mathrm{MN} = 2\sqrt{2} $$
$\mathrm{BP}$ の長さ
点 $\mathrm{P}$ は $\mathrm{OD}$ を 3 等分する点です。これは次の図の相似関係から分かります。
($\mathrm{BP}/\!/\mathrm{HQ}$ となるように点 $\mathrm{Q}$ を取りました。)
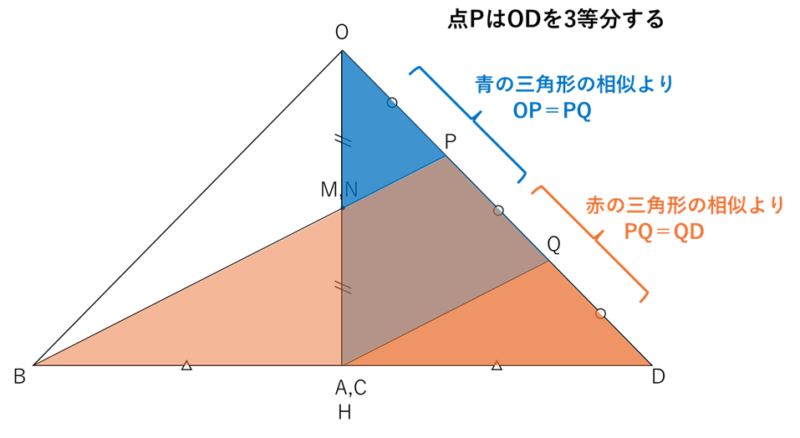
次に、直角三角形 $\mathrm{BPI}$ に着目します($\mathrm{I}$ は $\mathrm{P}$ から $\mathrm{BD}$ に下ろした垂線の足)。

高さ方向の比($\mathrm{OD}:\mathrm{PD}=3:2$)より、
$$ \mathrm{PI} = \frac{2}{3}\,\mathrm{OH} = \frac{4\sqrt{2}}{3} $$
底辺方向の比($\mathrm{HD}:\mathrm{HI}=3:1$)より、
$$ \mathrm{HI} = \frac{1}{3}\,\mathrm{BH} = \frac{2\sqrt{2}}{3} $$
よって、三平方の定理より
\[\mathrm{BP}^2 = \left(2\sqrt{2} + \frac{2\sqrt{2}}{3}\right)^2 + \left(\frac{4\sqrt{2}}{3}\right)^2 \\= \left(\frac{4\sqrt{2}}{3}\right)^2 \cdot 5\]
$$ \therefore\;\mathrm{BP} = \frac{4}{3}\sqrt{10} $$
以上より、切り口の面積は
\begin{eqnarray}
S &=& \frac12 \cdot \mathrm{MN} \cdot \mathrm{BP}\\
&=& \frac12 \cdot 2\sqrt{2} \cdot \frac{4}{3}\sqrt{10} = \frac{8}{3}\sqrt{5}
\end{eqnarray}
解(3). 切断上側の体積
(3) 2 つに分けた立体のうち、点 $\mathrm{O}$ を含む方の体積を求めよ。
ここでは(2)まで解いてきた誘導に従い、底面を四角形 $\mathrm{BMPN}$ と見て高さ $\mathrm{OJ}$ を求める方法で体積を計算します。後で、よりシンプルな別解も紹介します。
平面 $\mathrm{OBD}$ で立体を切って考えます。そして、$\mathrm{O}$ から $\mathrm{BP}$ に下ろした垂線の足を $\mathrm{J}$ とします。

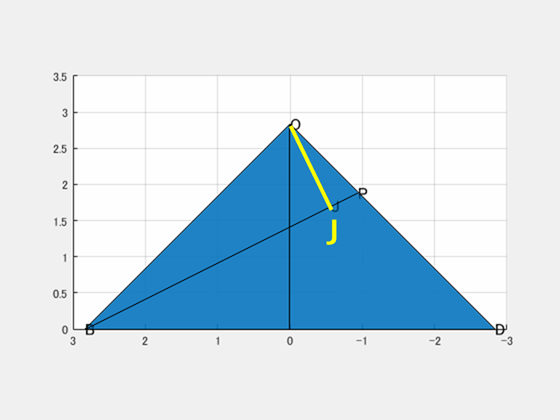
点 $\mathrm{B}$ を原点とする座標平面を考えます。すると、(1)(2) の結果から点 $\mathrm{O}$、$\mathrm{D}$、$\mathrm{P}$ の座標が決まります。

直線 $\mathrm{BP}$ の傾きは $\displaystyle\frac12$ なので、これに垂直な直線 $\mathrm{OJ}$ の傾きは $-2$ です。したがって、$\mathrm{OJ}$ の式は
$$ y = -2(x – 2\sqrt{2}) + 2\sqrt{2} $$
この「傾きと1点で一行で書く」直線の式の出し方は、次の記事で詳しく解説しています。
直線 $\mathrm{BP}$ と直線 $\mathrm{OJ}$ の交点が $\mathrm{J}$ なので、
- 直線 $\mathrm{BP}:y=\displaystyle\frac12x$
- 直線 $\mathrm{OJ}:y = -2(x – 2\sqrt{2}) + 2\sqrt{2}$
この連立方程式を解くと(WolframAlphaに解かせる)
$$ \mathrm{J}\left(\frac{12}{5}\sqrt{2},\; \frac{6}{5}\sqrt{2}\right) $$
よって、$\mathrm{OJ}$ の長さは
$$ \mathrm{OJ}^2 = \left(\frac{12}{5}\sqrt{2} – 2\sqrt{2}\right)^2 + \left(\frac{6}{5}\sqrt{2} – 2\sqrt{2}\right)^2 $$
$$ = \left(\frac{2}{5}\sqrt{2}\right)^2 + \left(\frac{4}{5}\sqrt{2}\right)^2 = \left(\frac{2}{5}\sqrt{2}\right)^2 \cdot 5 $$
$$ \therefore\;\mathrm{OJ} = \frac{2}{5}\sqrt{10} $$
したがって、求める体積は
\begin{eqnarray}
V &=& \frac13 \cdot S \cdot \mathrm{OJ}\\
&=& \frac13 \cdot \frac{8}{3}\sqrt{5} \cdot \frac{2}{5}\sqrt{10} = \frac{16}{9}\sqrt{2}
\end{eqnarray}
別解:底面の捉え方を変える
誘導に従って高さ $\mathrm{OJ}$ を求める方法でも体積は求められますが、実はもっとシンプルに体積比を求める方法があります。
それは、立体を $\mathrm{OBD}$ で縦半分に割り、底面を $\mathrm{OCD}$ と見る方法です。
三角形 $\mathrm{ONP}$ は三角形 $\mathrm{OCD}$ の $\displaystyle\frac{1}{6}$ です。


つまり、底面積が $\displaystyle\frac{1}{6}$ になるので、体積もそのまま $\displaystyle\frac{1}{6}$ になります。
($\displaystyle\frac16 = \displaystyle\frac12 \cdot \displaystyle\frac13$)
元の正四角錐の体積は
$$ V_{\mathrm{O\!-\!ABCD}} = \frac13 \cdot \frac12 \cdot \mathrm{AC} \cdot \mathrm{BD} \cdot \mathrm{OH} = \frac{32}{3}\sqrt{2} $$
したがって、求める体積は
$$ V = \frac16 \cdot V_{\mathrm{O\!-\!ABCD}} = \frac{16}{9}\sqrt{2} $$
まとめ
正四角錐を平面 $\mathrm{BMN}$ で切断し、切り口の面積と体積を求めました。
ポイントは次の 5 つです。
- 高さ $\mathrm{OH}$ は三平方の定理で求まる。
- 切り口の面積は $\displaystyle\frac12 \cdot \mathrm{MN} \cdot \mathrm{BP}$ で求まる。
- $\mathrm{P}$ が $\mathrm{OD}$ を三等分することは、相似で理解できる。
- 高さ($\mathrm{OJ}$)を求めるのは大変。座標を持ち出した。
- 別解として、体積は底面の捉え方を変えると比だけで一瞬で求まった。
問題2:正四角錐の切断2(底面の辺から切断)
図のように、1 辺がすべて 8cm の正四角錐 $\mathrm{OABCD}$ があり、辺 $\mathrm{OB}$ の中点を $\mathrm{P}$ とする。この正四角錐を 3 点 $\mathrm{A}$, $\mathrm{D}$, $\mathrm{P}$ を通る平面で切ったとき、

(1) 正四角錐 $\mathrm{OABCD}$ の体積を求めよ。
(2) 切り口の図形の面積を求めよ。
(3) 2 つに分けた立体のうち、点 $\mathrm{O}$ を含む方の体積を求めよ。
(21年 東海高校)
まずは切断のイメージをつかみましょう。次のアニメーションを見ると、平面 $\mathrm{ADP}$ がどのように立体を貫いているかが分かります。
解(1). 正四角錐の体積
(1) 正四角錐 $\mathrm{OABCD}$ の体積を求めよ。
問題1と同様に、点 $\mathrm{O}$ から底面に下ろした垂線の足を $\mathrm{H}$ とします。問題1の正四角錐は 1 辺が 4cm でしたが、今回はその 2 倍なので、高さも 2 倍になります。
$\mathrm{OH} = 4\sqrt{2}$
底面の面積は $8\times 8 = 64$ なので、体積は
$$V=\frac13\cdot 64\cdot 4\sqrt{2}=\frac{256}{3}\sqrt{2}$$
解(2). 切り口の面積
(2) 切り口の図形の面積を求めよ。
切り口は四角形 $\mathrm{ADQP}$ です($\mathrm{Q}$ は辺 $\mathrm{OC}$ と切断平面との交点)。
これは台形なので、(上底+下底)×高さ÷2 で求められます。

台形の上底・下底
四角形 $\mathrm{ADQP}$ は台形で、上底・下底は
・$\mathrm{AD}=8$(問題文より)
・$\mathrm{PQ}=4$($\mathrm{BC}$ の中点を通るため)
台形の高さ
あとは台形の高さ $\mathrm{PR}$ を求めます($\mathrm{R}$ は $\mathrm{P}$ から $\mathrm{AD}$ に下ろした垂線の足)。

まず、左図より $\triangle \mathrm{APB}$ は直角三角形なので、
$$\mathrm{AP}=4\sqrt{3}$$
次に、右図の直角三角形 $\triangle \mathrm{PRA}$ に三平方の定理を使うと、
$$\mathrm{PR}=\sqrt{44}=2\sqrt{11}$$
台形の面積
よって、台形 $\mathrm{ADQP}$ の面積は
$$S=\frac12(8+4)\cdot 2\sqrt{11}=12\sqrt{11}$$
解(3). 切断上側の体積
(3) 2 つに分けた立体のうち、点 $\mathrm{O}$ を含む方の体積を求めよ。
ここでは(2)まで解いてきた誘導に従い、底面を四角形 $\mathrm{ADQP}$ と見て高さ $\mathrm{OJ}$ を求めます。後で、よりシンプルな別解も紹介します。
$\mathrm{AD}$ と $\mathrm{BC}$ の中点をそれぞれ $\mathrm{S}$, $\mathrm{T}$ とし、平面 $\mathrm{OST}$ で立体を切ります。$\mathrm{O}$ から底面に下ろした垂線の足を $\mathrm{J}$ とします。

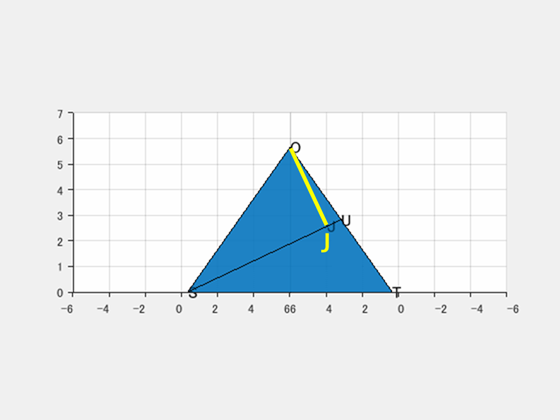
点 $\mathrm{S}$ を原点とする座標平面で考えます。すると、(1)(2) の結果から点 $\mathrm{O}$、$\mathrm{T}$、$\mathrm{U}$ の座標が決まります。

直線 $\mathrm{SU}$ の傾きは $\displaystyle\frac{\sqrt{2}}{3}$、これに垂直な直線 $\mathrm{OJ}$ の傾きは $-\displaystyle\frac{3}{\sqrt{2}}$ です。したがって、$\mathrm{OJ}$ の式は
$$y=-\frac{3}{\sqrt{2}}(x-4)+4\sqrt{2}$$
直線 $\mathrm{SU}$ と直線 $\mathrm{OJ}$ の交点が $\mathrm{J}$ なので、
- 直線 $\mathrm{SU}:y=\displaystyle\frac{\sqrt{2}}{3}x$
- 直線 $\mathrm{OJ}:y=-\displaystyle\frac{3}{\sqrt{2}}(x-4)+4\sqrt{2}$
この連立方程式を解くと(WolframAlphaに解かせる)
計算すると
$$\mathrm{J}\left(\frac{60}{11},\frac{20}{11}\sqrt{2}\right)$$
よって $\mathrm{OJ}$ の長さは
\begin{eqnarray}
\mathrm{OJ}^2 &=& \left(\frac{60}{11}-4\right)^2 +\left(\frac{20}{11}\sqrt{2}-4\sqrt{2}\right)^2\\
&=&\left(\frac{8}{11}\right)^2\cdot 22
\end{eqnarray}
$$\therefore\;\mathrm{OJ}=\frac{8}{11}\sqrt{22}$$
したがって、求める体積は
\[ V=\frac13\cdot 12\sqrt{11}\cdot \frac{8}{11}\sqrt{22} =32\sqrt{2} \]
別解:底面の捉え方を変える
誘導に従う方法でも体積は求められますが、問題1と同様に、底面の捉え方を変えると体積比だけで一瞬で求められます。

三角形の対応より、
\[ \triangle\mathrm{ODQ}=\frac12\triangle\mathrm{ODC},\qquad \triangle\mathrm{OPQ}=\frac14\triangle\mathrm{OBC} \]
よって体積比は
$$\frac12\left(\frac12+\frac14\right)=\frac38$$
元の体積 $\displaystyle\frac{256}{3}\sqrt{2}$ の $\displaystyle\frac38$ なので、
$$V=32\sqrt{2}$$
まとめ
正四角錐を底面の辺と隣の辺の中点を結ぶ平面で切断しました。
問題1と同様、まずは 高さは三平方の定理で一瞬で求まる ことを押さえましょう。
そのうえで、誘導に従って切り口の面積と高さを求める方法と、底面の捉え方を変えて体積比で求める 別解 の両方を経験しておくと、空間図形の見え方が大きく広がります。
問題3:四角柱の角を切り落とす
問題文は長いので問題の要点を示すと、
青の直方体に対し、$\mathrm{PQR}$ で切り取られた四面体の辺の長さは $t$ 秒後、
$\mathrm{FP}=4-t$, $\mathrm{FQ}=t$, $\mathrm{FR}=2t$
です。この3本の長さが、$\mathrm{PQR}$ の変化を理解するカギになります。
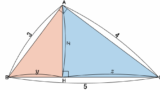
図の立体 $\mathrm{ABCD}-\mathrm{EFGH}$ は、正方形 $\mathrm{ABCD}$ を底面とし、$\mathrm{AB}=4\mathrm{cm}$, $\mathrm{AE}=8\mathrm{cm}$ の直方体である。図のように、辺 $\mathrm{EF}$ 上を動く点 $\mathrm{P}$ は、頂点 $\mathrm{E}$ を出発して毎秒 $1\mathrm{cm}$ の速さで点 $\mathrm{F}$ に到達するまで動き、辺 $\mathrm{FG}$ 上を動く点 $\mathrm{Q}$ は、頂点 $\mathrm{F}$ を出発して毎秒 $1\mathrm{cm}$ の速さで点 $\mathrm{G}$ に到達するまで動き、辺 $\mathrm{FB}$ 上を動く点 $\mathrm{R}$ は、頂点 $\mathrm{F}$ を出発して毎秒 $2\mathrm{cm}$ の速さで点 $\mathrm{B}$ に到達するまで動く。3 点 $\mathrm{P}$, $\mathrm{Q}$, $\mathrm{R}$ が同時に出発するとき、

(1) $\triangle\mathrm{PQR}$ が二等辺三角形になるのは何秒後と何秒後か?
(2) 1 秒後のときの四面体 $\mathrm{FPQR}$ の頂点 $\mathrm{F}$ から底面 $\mathrm{PQR}$ に下した垂線の長さは何 $\mathrm{cm}$ か?
(20年 東海高校)
まずは三角形 $\mathrm{PQR}$ がどのように変化していくか、イメージをつかみましょう。次のアニメーションを見ると、三角形が時間とともにどのように形を変えるかが分かります。(二等辺になる瞬間は 2 回あります。)
(2) は、四面体の体積を使って高さを求めます。
解(1). 二等辺三角形になる時刻
$t$ 秒後の辺の長さ
ここでは、三角形 $\mathrm{PQR}$ の 3 辺の長さを時間 $t$ の式で表し、二等辺三角形になる時刻を求めます。
$t$ 秒後の長さは
$\mathrm{FP}=4-t$, $\mathrm{FQ}=t$, $\mathrm{FR}=2t$
したがって、三平方の定理より、
- $\mathrm{PQ}^2 =$ $(4-t)^2$$+$$t^2$$ = 2t^2-8t+16$
- $\mathrm{QR}^2 =$ $t^2$$+$$(2t)^2$$ = 5t^2$
- $\mathrm{RP}^2 =$ $(2t)^2$$+$$(4-t)^2$$ = 5t^2-8t+16$
二等辺三角形になるのは、$\mathrm{PQ}=\mathrm{QR}$, $\mathrm{QR}=\mathrm{RP}$, $\mathrm{RP}=\mathrm{PQ}$ のいずれかです。
$\mathrm{PQ}=\mathrm{QR}$ の場合
$2t^2-8t+16=5t^2$
\begin{eqnarray} 3t^2+8t+16=0\\ (3t-4)(t+4)=0 \end{eqnarray}
$t=\displaystyle\frac{4}{3}$($t>0$ より)
$\mathrm{QR}=\mathrm{RP}$ の場合
$5t^2=5t^2-8t+16$ より
$t=2$
$\mathrm{RP}=\mathrm{PQ}$ の場合
$5t^2-8t+16=2t^2-8t+16$ より
$3t^2=0$
$t=0$ となり、題意に合わない。
よって、二等辺三角形になるのは
$\displaystyle\frac{4}{3}$ 秒後 と 2 秒後。
解(2). 頂点 $\mathrm{F}$ から底面 $\mathrm{PQR}$ に下ろした垂線の長さ
ここでは、四面体 $\mathrm{FPQR}$ の体積を 2 通りの方法で表し、高さを求めます。
1 秒後の位置関係は次の図の通りです。

底面を直角三角形と見た体積(例えば $\triangle\mathrm{PQF}$)
このとき、$\mathrm{FP}=3$, $\mathrm{FQ}=1$, $\mathrm{FR}=2$ なので、四面体 $\mathrm{FPQR}$ の体積は
$$V=1\tag{1}\label{eq1}$$
底面を $\triangle\mathrm{PQR}$ と見る
次に、底面を $\triangle\mathrm{PQR}$ と見て、その面積を求めます。
三平方の定理より、
\[\mathrm{PR}^2=\mathrm{PF}^2+\mathrm{FR}^2=3^2+2^2=13\\
\mathrm{RQ}^2=\mathrm{RF}^2+\mathrm{FQ}^2=2^2+1^2=5\\
\mathrm{QP}^2=\mathrm{QF}^2+\mathrm{FP}^2=1^2+3^2=10\]

$\mathrm{Q}$ から $\mathrm{PR}$ に下ろした垂線の足を $\mathrm{H}$ とし、$\mathrm{PH}=x$, $\mathrm{QH}=y$ と置きます。
直角三角形 $\triangle\mathrm{QHP}$, $\triangle\mathrm{QHR}$ に三平方の定理を適用すると、
\begin{eqnarray}
\left\{\begin{array}{l}
10 = x^2+y^2\\
5 = (\sqrt{13}-x)^2+y^2
\end{array}\right.
\end{eqnarray}
この連立方程式を解くと(WolframAlphaに解かせる)
\begin{eqnarray} x=\frac{9}{\sqrt{13}},\qquad y=\frac{7}{\sqrt{13}} \end{eqnarray}
よって、底面積 $S$ は
$$S=\frac12\cdot \sqrt{13}\cdot \frac{7}{\sqrt{13}}=\frac{7}{2}\tag{2}\label{eq2}$$
既知の体積から高さを求める
体積の公式 $V=\displaystyle\frac13Sh$ に \eqref{eq1} \eqref{eq2} を代入すると、
\[ 1=\frac13\cdot \frac72\cdot h \]
$$\therefore\;h=\frac{6}{7}$$
解説1:四面体の高さを求めるアイデアについて
体積を2通りの見方で表現することにより高さを求めました。これを2次元で説明した下記の記事が参考になります。
解説2:△PQRの高さを求めるアイデアについて
三辺の長さが既知の場合の高さです。下記の記事の「基本その2」もその発想です。
まとめ
四角柱の角を切り落としました。
三辺の長さが分かっている三角形の高さは、三平方の定理を2回適用することで求められます。


また、平面に下した垂線の長さは、体積を 2 通りに捉えることで求められることも確認しました。下記はこの発想を平面図形で確認する記事です。
まとめ
3つの問題を通して、空間図形の見方が大きく整理されました。
- 高さは三平方の定理で一瞬で求まる。(問題1,2)
- 切り口は空間のままでは構造がつかみにくいが、
「台形として見られないか」「二等辺三角形として捉えられないか」と眺め直すと、
図形の特徴、長さや平行、高さの関係が一気に見えるようになる。(問題1,2) - 直線の式は「傾き+1点」で一行で書ける。(問題1,2)
- 体積は底面の捉え方を変えると一気に求まる。(問題1,2の別解)
- 錐体の高さは体積の逆算で求められる。(問題3)
空間図形は、まずイメージ、次に構造、最後に計算。この流れを押さえておくと、どんな問題でも安定して解けるようになります。



コメント