運動エネルギーの公式はなぜ1/2なのか？ 運動量、力積との違いは？

　運動エネルギーの公式は次の式です。

$W$ は与えた仕事であり、この仕事によりもともと持っていた運動エネルギー $\displaystyle\frac{1}{2}mv_0^2$ が $\displaystyle\frac{1}{2}mv^2$ になった、というものです。

ここではこの公式を仕事の定義から導くことにより、その意味を考えてみます。とはいっても、式変形をひたすらに行ってもつらいだけなので、できるだけ「パッと見」で理解できるように工夫します。その分記号の説明は省略する部分があります。

　こちらの記事↓も参考にしてください。↓は運動エネルギーだけではなく、力学的エネルギー全般について論じています。

運動エネルギーの公式を仕事の定義から導く

　次のような状況を想定します。

すなわち、あなたの手が力 $F$ で質量 $m$ の物体を距離 $x$ だけ引っ張ります。距離 $x$ だけ引っ張ったことにより初速度 $v_0$ が速度 $v$ に変化しました。摩擦は無いとします。

さてここで、あなたの手が行った「仕事」は物体にどのような形で乗り移ったのかを考えます。

簡単のため、等加速度運動を前提にして考える

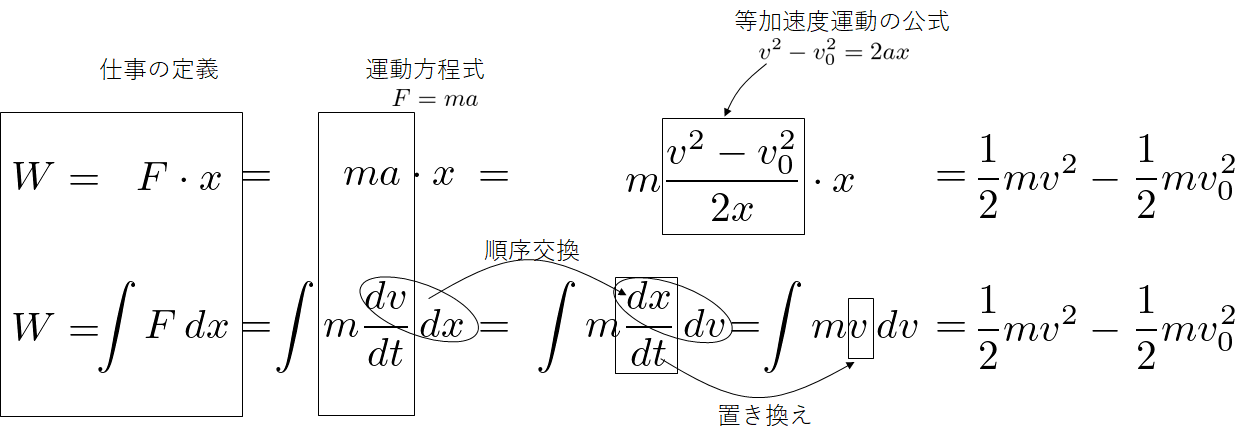
　結論を一行で示すと次のようです。ここでは簡単のために一定の力を加えており、従って物体は等加速度運動をしているとします。

つまり、

• 仕事の定義から出発し、
• 運動方程式を用い、
• 式変形をしていくことにより
• $\displaystyle\frac{1}{2}mv^2$ の形が表れる

ということになります。

なぜ $\displaystyle\frac{1}{2}$ が表れるのかと問われれば、仕事の定義を式変形した結果、というのが一番正しいのですが、あえてその意味を解釈すれば、$\displaystyle\frac{1}{2}$ が等加速度運動の公式の右辺の係数 $2$ に由来していることに依ります。そして等加速度運動でなぜ $2$ が係数として出てきたのかと思い出せば、この公式は次の式から $t$ を消去したものですので、

• $v=v_0+at$
• $x=v_0t+\displaystyle\frac{1}{2}at^2$

それはつまり、速度を積分した結果として $\displaystyle\frac{1}{2}$ が出てきていることになります。しかしこれもまた「式変形した結果」ということにはなってしまうので、これもまたあえてその意味を解釈すれば、距離 $x$ は $v-t$ グラフで描かれる三角形（もしくは台形）の面積であり、それはつまり初めは遅くだんだん速くなっていくことを反映していると言えます。

また、同様にエネルギーが $v$ の2乗であることも理解できます。これは、距離 $x$ は時間の2乗に比例して伸びていき、速度は時間に比例して伸びていくため、距離をベースにした仕事は速度の2乗に比例することになります。

一般形で考える

　ここでは加える力は一定とは限らない一般の場合で考えます。結論を一行で示すと次のようです。

つまり、これも先と同様、

• 仕事の定義から出発し、
• 運動方程式を用い、
• 式変形をしていくことにより
• $\displaystyle\frac{1}{2}mv^2$ の形が表れる

ということになります。

↓の記事ではここで述べた一般形で最初から説明をしています。

まとめ

　等加速度運動の場合もそうでない場合も同じ結果になりました。まとめとして両者を比較します。

運動エネルギーの導出から見る力学的エネルギー保存の法則

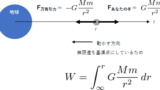
　上記の導出では仕事は「あなたの手」が行いましたが、これは説明都合上だけの話であり、この仕事を「重力」が行えば力学的エネルギー保存の法則になります。

すなわち、重力による位置エネルギーの問題では、力学的エネルギー保存の法則を用いて問題を解くのと、等加速度運動の公式を用いて問題を解くのとは実は同じである、ということが分かります。

運動量との関係

　運動エネルギーに対して運動量という物理量もあります。まず、この両者を整理します。

これらはどちらも力 $F$ が与えられた結果得られる速度 $v$ を用いて表現する物理量であり、どのように違うのか分かりづらいですね。

運動エネルギーは、上記で見たように仕事の定義から導かれました。一方、運動量は力積の定義から導かれます。運動エネルギーの導出と並べて書き表すと次のようです。

すなわち、

• 仕事は力を距離で積分
• 力積は力を時間で積分

した違いがあるということになります。最右辺の量と絡めて表現すれば、

• 仕事をした分だけ運動エネルギーが変化する
• 力積を加えた分だけ運動量が変化する

ということですが、どちらももとをただせば同じ力 $F$ が起源になっているのに違う物理量が出てくるところがモヤモヤするのではないかと思います。

しかしこれはそういうものだと理解するしかないような気がします。

• 力と距離が大切な物理量があり、それが仕事であり、それは運動エネルギーを変化させる
• 力と時間が大切な物理量があり、それが力積であり、それは運動量を変化させる

そしてその両者はそれぞれ、

• エネルギー保存の法則、や
• 運動量保存の法則

といった独自の法則を持つ。ということになると思います。

まとめ

　運動エネルギーが係数 $\displaystyle\frac{1}{2}$ を持つことにフォーカスを当てて運動エネルギーの公式の成り立ちを考えました。また同時に $v^2$ が出てくる理由も考えました。

$v^2$ が出てくるのは、仕事は距離に比例する一方、速度を2倍にするには引っ張る距離をその2乗の4倍にしないといけないからです。これは次の比例関係からそうなりますが、直感的には、すでに速度を持っている状態からさらに同じ力で引っ張ると、速度を持っていないときから引っ張るよりも距離は当然伸びるということです。

係数 $\displaystyle\frac{1}{2}$ が出てくるのは、距離 $x$ は $v-t$ グラフで描かれる三角形（もしくは台形）の面積であり、それはつまり初めは遅くだんだん速くなっていくことを反映しています。

これらを合わせて整理すると次の式変形となります。

類似記事として↓の記事も見てみてください。こちらは力学的エネルギー保存の法則にスポットを当てて解説しています。