二次関数の問題は入試で頻出分野です。前記事では5つの頻出パターンを会得しました。今回はそれらがしっかりとマスターできたかどうか、実際の入試問題で確認をしましょう。前記事はこちら↓です。
ここでは実際に出された入試問題の中で面積問題の部分だけをピックアップしました。とは言いつつ実際には、面積問題にたどり着く前にはもっと基本的な問題が並んでいますので、まずはそこを確実に解き、その上で差がつくこの部分を取る、そういう戦略で行きましょう。面積問題の部分も復習しやすくするために問題文を端折ったりしていますので、実際の問題はどのようなのか確認できるよう、リンクをつけました。
問題1：22年 大阪星光学院
$\triangle\mathrm{AOD}=\triangle\mathrm{APD}$ となる点 $\mathrm{P}$ の座標は？
点 $\mathrm{P}$ は点 $\mathrm{C}$ から点 $\mathrm{D}$ の間にあり、点 $\mathrm{O}$ とは異なる。
前年分の掲載のみのようです。↑の問題はもうないです。
イメージ
解
$\mathrm{AB}$ の傾きは $\displaystyle\frac{1}{2}$ なので、求める点 $\mathrm{P}$ は、$y=\displaystyle\frac{1}{2}x$ と $y=x^2$ との $\mathrm{O}$ ではない交点である。
よって、
\begin{eqnarray}
\left\{ \begin{array}{l}
y &=& x^2\\
y &=& \displaystyle\frac{1}{2}x
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
\begin{array}{c}
x^2 = \displaystyle\frac{1}{2}x\\
2x^2-x=0\\
x(2x-1)=0\\
x=\displaystyle\frac{1}{2}\quad (\because 点 \mathrm{P} は 点 \mathrm{O} とは異なるので\, x\ne 0)
\end{array}
\end{eqnarray}
$$\therefore\;\mathrm{P}(\frac{1}{2},\frac{1}{4})$$
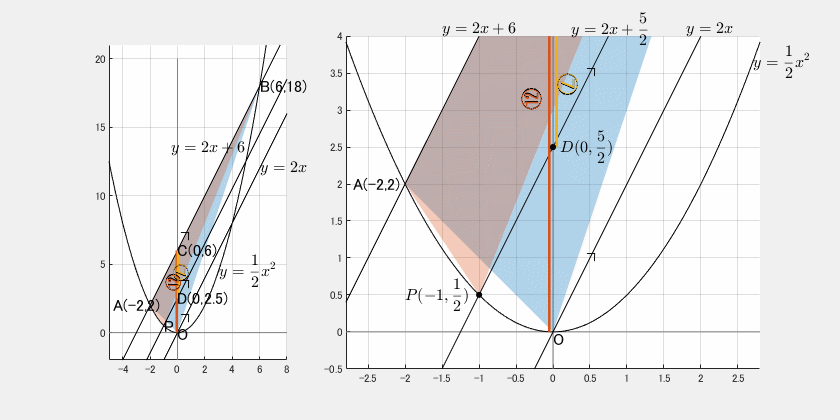
問題2：23年 西大和学園
$\triangle\mathrm{OAB}:\triangle\mathrm{PAB}=12:7$ のとき、$\mathrm{P}$ の座標は？
$\mathrm{P}$ は $y=\displaystyle\frac{1}{2}x^2$ 上で $\mathrm{OA}$ 間にあるものとする。
イメージ
解
$\triangle\mathrm{OAB}:\triangle\mathrm{PAB}=12:7$ より $\mathrm{AB}$ を底辺として、
$\triangle\mathrm{OAB}$ の高さ $: \triangle\mathrm{PAB}$ の高さ $= 12:7$
になればよく、それは、$y$ 軸上の長さで測ればよい。すなわち、$\mathrm{CO}=\displaystyle\frac{12}{2}$ より、$\mathrm{CD}=\displaystyle\frac{7}{2}$ なる点 $\mathrm{D}$、つまり
$\mathrm{D}(0,\displaystyle\frac{5}{2})$
を取って、話を続ける。
すると、点 $\mathrm{P}$ は、
点 $\mathrm{D}$ を通り、傾きが $\mathrm{AB}$ に等しい直線上
にある。すなわち、
$$ y=2x+\frac{5}{2}$$
上にある。
加えて点 $\mathrm{P}$ は $y=\displaystyle\frac{1}{2}x^2$ 上でもあるから、求める点 $\mathrm{P}$ は両者の連立方程式の解である（ただし、問題文より $\mathrm{OA}$ 上に限定される）。よって、
\begin{eqnarray}
\left\{ \begin{array}{l}
y &=& \displaystyle\frac{1}{2}x^2\\
y &=& 2x+\displaystyle\frac{5}{2}
\end{array}
\right.
\end{eqnarray}
より $y$ を消去して、
\begin{eqnarray}
\begin{array}{c}
\displaystyle\frac{1}{2}x^2 = 2x+\displaystyle\frac{5}{2}\\
x^2-4x-5=0\\
(x+1)(x-5)=0\\
\therefore\; x=-1\quad (\because \text{点 }\mathrm{P}\text{ は }\mathrm{OA}\text{ 上})
\end{array}
\end{eqnarray}
問題3：23年 成城学園
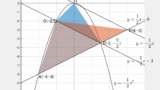
$\triangle\mathrm{OAB}$ を二等分する直線 $y=k$ の $k$ は？
イメージ
解
$y=1$ と $\mathrm{OA}$ の交点を $\mathrm{Q}$ と置くと、
明らかに $\triangle\mathrm{OQB}<\triangle\mathrm{AQB}$ より、直線 $y=k$ は $y=1$ より上であり、かつ点 $\mathrm{A}\;(y=4)$ よりも下であるから、
$$1<k<4$$
である。
従って、$y=k\;(1<k<4)$ と $\mathrm{OA}$, $\mathrm{AB}$ の交点 $\mathrm{Q}$, $\mathrm{R}$ の座標は
\begin{eqnarray}
\begin{array}{c}
\mathrm{Q}(-k,k)\\
\mathrm{R}(4-2k,k)
\end{array}
\end{eqnarray}
と置ける。$(\rightarrow\text{解説1:丁寧に求める})$
このとき、
\begin{eqnarray}
\triangle\mathrm{AQR} &=& \left\{(4-2k)-(-k)\right\}\times(4-k)\times\frac{1}{2}\\
&=& (4-k)\times (4-k)\times\frac{1}{2}\\
&=& \frac{1}{2}(4-k)^2
\end{eqnarray}
これが $\triangle\mathrm{OAB}$ の面積 $6$ の半分になればよいから、
$(\rightarrow\text{解説2:}\triangle\mathrm{OAB}\text{の面積})$
\begin{eqnarray}
\begin{array}{c}
\displaystyle\frac{1}{2}(4-k)^2 = 3\\
(4-k)^2=6\quad (\rightarrow\text{解説3})\\
4-k = \pm\sqrt{6}\\
\therefore\; k=4-\sqrt{6}\quad (\because k<4)\quad (\rightarrow\text{解説4})
\end{array}
\end{eqnarray}
よって、求める直線は、
$$y=4-\sqrt{6}$$
解説1. 点 $\mathrm{Q}$, $\mathrm{R}$ の座標を丁寧に求める：直線 $\mathrm{AB}$ の式は一行で求めよう
点 $\mathrm{Q}$ の座標
まず、点 $\mathrm{Q}$ はすぐに求められると思います。直線 $\mathrm{OA}$ の式が
$$y=-x$$
であり、その $y=k$ のときの $x$ を求めればよいので、
$$x=-k$$
$$\therefore\;\mathrm{Q}(-k,k)$$
点 $\mathrm{R}$ の座標
直線 $\mathrm{AB}$ の式を求めますが、傾きが求められればその式は一行で求められます。この記事↓で述べています。
直線 $\mathrm{AB}$ は傾き $-\displaystyle\frac{3}{6}(=-\textstyle\frac{1}{2})$ で点 $(2,1)$ を通るので、
\begin{eqnarray}
y &=& -\frac{1}{2}(x-2)+1\\
&=& -\frac{1}{2}x+2
\end{eqnarray}
と、一行で（二行ですが、式としては一本で）求められます。
解説2. $\triangle\mathrm{OAB}$ の面積
$\triangle\mathrm{OAB}$ の面積は、
\begin{eqnarray}
\triangle\mathrm{OAB} &=& 2\times 6\times\frac{1}{2}\\
&=& 6
\end{eqnarray}
で求められます。
解説3. 計算は工夫しよう（展開しない）
もちろん展開しても解けますが、展開しなくても解けます。展開して解いても、
\begin{eqnarray}
\begin{array}{c}
16-8k+k^2=6\\
k^2-8k+10=0\\
k=4\pm\sqrt{16-10}=4\pm\sqrt{6}
\end{array}
\end{eqnarray}
となり、もちろん同じ結果にはなりますが、展開しない方が楽に解けます。
細かいことではありますが、このような工夫ができるかどうかで計算の速さや正確性がかなり変わります。
解説4. $+$ の方はどうなった？
$+$ の方は $\mathrm{A}$ の上側に三角形を作ることを意味します。もちろんこれは $\triangle\mathrm{OAB}$ を二等分するものではないので不適切です。
この不適切なものを排除するために
$$1<k<4$$
の記述があります。特に、$k<4$ です。
問題4. 23年 奈良大学附属
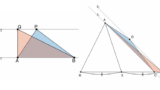
四角形 $\mathrm{OAPB}$ の面積が、平行四辺形 $\mathrm{ABOC}$ の面積の2倍になるとき、点 $\mathrm{P}$ の座標を全て求めよ。
解
題意を満たすためには下図のような面積配分になればよい。
すなわち、
$$\triangle\mathrm{OAB}:\triangle\mathrm{PAB}=1:3$$
になればよい。この2つの三角形は底辺を共有しているので高さの比が $1:3$ になればよいから、
点 $\mathrm{P}$ の $y$ 座標は $8$
であればよい。点 $\mathrm{P}$ は $y=\displaystyle\frac{1}{2}x^2$ 上の点なので、$y$ 座標が $8$ となるのは、
$$(4,8),\; (-4,8)$$
である。
解説. 面積配分に気づけば簡単
面積問題パターン5選の記事↓のパターン3も同様の発想でした。いくつかの三角形に分割することで面積比が表れてきます。「困難は分割せよ」とデカルトも言っています。
まとめ
二次関数の問題は入試で頻出分野です。ここで上げた問題はいずれも設問中の後半に登場する問題です。前半には、$y=ax^2$ の $a$ の値を求めよ、とか、$\triangle\mathrm{OAB}$ の面積を求めよ、とかの問題ですのでまずはこれらは確実に正解し、そして後半のこれらの問題を解けるようにすることで差がつきます。まずは「型」「パターン」をしっかりとマスターすることが重要なので、↓の記事でそれを復習ください。
また、さらにダメ押しでもう一つ記事を書きました。↓こちらにも挑戦してください。
コメント