【円周角の定理】円周角は弧長である！入試や定期テスト頻出問題を徹底理解！！

　円周角を弧長で眺めることができるようになることを目的にします。そのためにイメージをしっかりと植えつけます。

円周角の定理とは、円周角は中心角の半分である、という定理で下記↓で解説していますが、入試や定期テストで出る際には実際に角度を求めさせるものがほとんどです。

ここでは実戦で役に立つ、弧長と円周角の関係について、しっかりとイメージすることを目的にします。

弧長は中心角であり円周角である

　まずはこの感覚を身につけましょう。直径の中心角は当然ながら $180^\circ$ であり、その円周角は半分の $90^\circ$ です。

これはこの図↑のように、半円を考えて、

• 半円の中心角は $180^\circ$
• 半円の円周角は $90^\circ$

という感覚を持ちましょう。

その上で、円弧が増減したときの中心角と円周角をアニメーションで確認します。

当たり前ですが、円弧が小さくなればその分中心角と円周角は小さくなり、大きくなれば大きくなります。その感覚を持つことが重要です。その際、

• 半円の中心角は $180^\circ$
• 半円の円周角は $90^\circ$

から始めて、弧長に応じて中心角と円周角が変化する感覚を持ちましょう。

演習問題

円周が等分されている場合

イメージ

　$\mathrm{A}$ は半円を3等分しています。また $\mathrm{B}$ は半円を半分にしています。これをイメージ化すると下記↓のようになります。

解

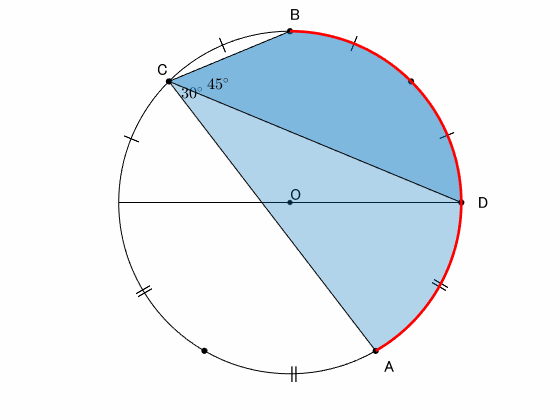
弧 $\overset{\frown}{\mathrm{AD}}$ の円周角は $30^\circ$

弧 $\overset{\frown}{\mathrm{BD}}$ の円周角は $45^\circ$

であるから、弧 $\overset{\frown}{\mathrm{AB}}$ の円周角は $75^\circ$

既知の円周角がある場合

イメージ

　円周を、既知の円周角 $40^\circ$ に対する弧とその排他部分の弧に分けたとき、排他部分の弧に対する円周角は $180-40=140^\circ$ です。その上、求めたい円周角は排他円周角 $140^\circ$ の半分であることに気づけばOKです。

解

弧 $\overset{\frown}{\mathrm{BFC}}$ の円周角 $\angle\mathrm{BAC}=40^\circ$ より、その反対側の弧 $\overset{\frown}{\mathrm{BAC}}$ の円周角は $140^\circ$ である。

ここで、求めたい円周角 $\angle\mathrm{DFE}$ に対するの弧長 $\overset{\frown}{\mathrm{DAE}}$ は $\overset{\frown}{\mathrm{BAC}}$ の半分であるから、求めたい円周角は

$$140\div 2 = 70^\circ$$

円周を付け足す発想

イメージ

　半円の円周角は $90^\circ$ です。$\angle\mathrm{ADC}=110^\circ$ は半円に弧 $\overset{\frown}{\mathrm{BC}}$ を加えた円周角であることに気づけばOKです。

解

$\angle\mathrm{ADC}=110^\circ$ は半円に弧 $\overset{\frown}{\mathrm{BC}}$ を加えた円周角であるから、弧 $\overset{\frown}{\mathrm{BC}}$ に対する円周角の大きさは、

$$110-90=20^\circ$$

である。

一方、求めたい角 $\angle\mathrm{BAD}$ は弧 $\overset{\frown}{\mathrm{BC}}=20^\circ$ の2倍の弧長の円周角なので、

$$\angle\mathrm{BAD}=20\times 2=40^\circ$$

入試例

帝塚山学院泉が丘高校 2025年度

2025kou-mondai-sugaku.pdf

イメージ

　求めたい角 $\angle\mathrm{BCD}$ を円周角の定理を使って移動させるところから始めます。

解

　$\angle\mathrm{BCD}=\angle\mathrm{BAD}$

$\overparen{\mathrm{BD}}=\overparen{\mathrm{DE}}$ より

$$\angle\mathrm{BAD}=\angle\mathrm{DAE}$$

ここで、$\triangle\mathrm{BAE}$ は直角三角形なので、$\angle\mathrm{ABE}=42^\circ$ とから、

$$\angle\mathrm{BAE}=48^\circ$$

求めたい角 $\angle\mathrm{BCD}$ は $\angle\mathrm{BAE}$ の半分なので、

$$\angle\mathrm{BCD}=24^\circ$$

まとめ

　円周角の定理の実践的な問題を取り上げました。弧長がそのまま中心角や円周角に対応付けられるようにイメージしましょう。

円周角の定理そのものの解説、証明は下記↓の記事で述べています。

また、円周角の定理の入試問題例は他に下記↓の記事で述べています。