【京都大学 文系 2024】対称性で読み解く空間ベクトルの体積問題｜図解で直感！

京都大学（文系）の空間ベクトル問題は、対称性をうまく使えば解決の糸口がつかめる、非常に美しい問題です。対称性をイメージしてもらいたいので、アニメーションを交えながら丁寧に理解していきます。

京都大学文系（24年度）

方針

長さや角度に条件があるので点の位置はかなり限定されます。 まずはその制約を一つずつ具体化していきます。

• $\mathrm{OA}=\mathrm{OB}=1$, $\angle{\mathrm{AOB}}=90^\circ$ から点 $\mathrm{A}$, $\mathrm{B}$ を制限（仮置き）
• $\angle{\mathrm{COA}}=\angle{\mathrm{COB}}$ から点 $\mathrm{C}$ を制限
• $\mathrm{OC}=1$ から点 $\mathrm{C}$ をさらに制限

です。その上で、

• $\angle{\mathrm{COA}}=\angle{\mathrm{COB}}=\angle{\mathrm{ACB}}$

でとどめを刺します。

解答

対称性から $\mathrm{A}$, $\mathrm{B}$ の位置を仮置きする

$\mathrm{OA}=\mathrm{OB}=1$, $\angle{\mathrm{AOB}}=90^\circ$ から、$\mathrm{A}$ と $\mathrm{B}$ は次のように置けます。

$$\mathrm{A}(1,0,0),\quad \mathrm{B}(0,1,0)$$

さらに対称性から $\mathrm{C}$ の位置を限定する

$\angle{\mathrm{COA}}=\angle{\mathrm{COB}}$ という対称性から、点 $\mathrm{C}$ の $x$ 座標と $y$ 座標は等しく、

$$(p,\,p,\,〇)$$

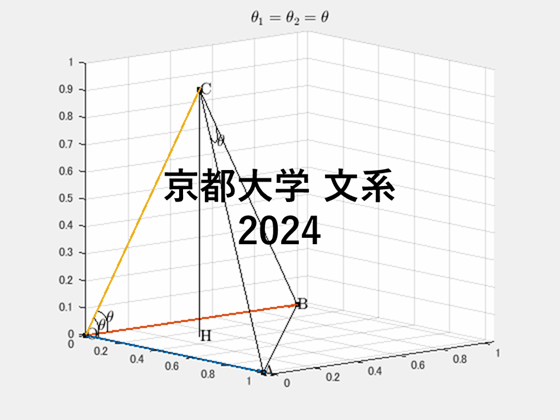
と限定できます。まずはこの立体のイメージをアニメーションで確認しましょう。

$\mathrm{C}$ の制約からさらに限定する

$\mathrm{OC} = 1$ なので、$\mathrm{C}$ の $z$ 座標は $\sqrt{1-2p^2}$ となり、

$$\mathrm{C}(p,p,\sqrt{1-2p^2})$$

と限定できます。

角度条件 $\angle{\mathrm{COA}}=\angle{\mathrm{COB}}=\angle{\mathrm{ACB}}$ を使う

このイメージは、

$\angle{\mathrm{COA}}=\angle{\mathrm{COB}}=\theta_1$ を変えたら
$\angle{\mathrm{ACB}}=\theta_2$ が変わる

ということで、このアニメーションです。

$\theta_1$ を表す

$\mathrm{A}(1,0,0)$, $\mathrm{C}(p,p,\sqrt{1-2p^2})$ なので、

\begin{eqnarray}
\cos\theta_1 &=& \frac{\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OC}}}{|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OC}}|}=\frac{\begin{pmatrix}1\\0\\0\end{pmatrix}\cdot\begin{pmatrix}p\\p\\\sqrt{1-2p^2}\end{pmatrix}}{1\times 1}\\
&=& p
\end{eqnarray}

$\theta_2$ を表す

$\mathrm{A}(1,0,0)$, $\mathrm{B}(0,1,0)$, $\mathrm{C}(p,p,\sqrt{1-2p^2})$ なので、

\begin{eqnarray}
\cos\theta_2 &=& \frac{\overrightarrow{\mathrm{CA}}\cdot\overrightarrow{\mathrm{CB}}}{|\overrightarrow{\mathrm{CA}}||\overrightarrow{\mathrm{CB}}|}=\frac{\begin{pmatrix}1-p\\-p\\-\sqrt{1-2p^2}\end{pmatrix}\cdot\begin{pmatrix}-p\\1-p\\-\sqrt{1-2p^2}\end{pmatrix}}{\left|\begin{pmatrix}1-p\\-p\\-\sqrt{1-2p^2}\end{pmatrix}\right|\cdot\left|\begin{pmatrix}-p\\1-p\\-\sqrt{1-2p^2}\end{pmatrix}\right|}\\
&=& \frac{1-2p}{2(1-p)}
\end{eqnarray}

方程式を解く

$p=\displaystyle\frac{1-2p}{2(1-p)}$ より、$p=\displaystyle\frac{2\pm\sqrt{2}}{2}$

$p=\cos\theta_1\le1$ に注意すると、

$$p=\frac{2-\sqrt{2}}{2}$$

体積を求める

$\mathrm{A}(1,0,0)$, $\mathrm{B}(0,1,0)$ より底面積は $\displaystyle\frac12$。

$\mathrm{C}(p,p,\sqrt{1-2p^2})$ より高さは $\sqrt{1-2p^2}$。$p$ の値を代入すると、$\displaystyle\sqrt{2\sqrt{2}-2}$。

よって体積 $V$ は

$$V = \frac{1}{6}\sqrt{2\sqrt{2}-2}$$

まとめ

他の入試問題にも挑戦してください：