この解法は学校ではおそらく出てきません。私自身も結構レベルの高い参考書で初めて出会い、こんな解法があるのかと感動したことを覚えています。その感動を、裏技と位置付けて皆さんに共有します。
$y=2tx-t^2$ の通過領域：$t$ が実数全体
【通過領域：順像法】【通過領域：逆像法】と同じ問題をここでは包絡線の解法で解きます。同じ問題を別の解法で解くことで、それぞれの解法のうまみ、特徴がよくわかると思います。
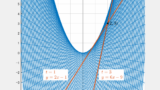
$t$ が実数全体を動くとき、直線 $y=2tx-t^2$ が通過する領域を図示せよ。
求める包絡線とは、
直線群 $y=2tx-t^2$ の全てに接している曲線
のことで、次のアニメーションで確認します。
この裏技的解法を3つ紹介します。1つ目と2つ目は裏技的とはいえ比較的素直な解法ですが、$t$ の2次式でしか使えない限定版です。3つ目はそれ以外でも使える万能版ですが、高校数学の範囲では超裏技的です。
解法1（初級裏技）：判別式を用いる方法
これは【通過領域：逆像法】とほぼ同じ発想の解法なので裏技ではないのですが、$D=0$ にすることにより接する情報を引き出しているところが興味深いです。しかし残念なことにこの解法は $t$ が二次式のときにしか使えません。
解
直線の式を $t$ で整理して
$$t^2-2xt+y=0\tag{1-1}\label{p3478eq1-1}$$
これを $t$ に関する二次方程式とみてその判別式を $D$ と置くと、
\begin{eqnarray}
\frac{D}{4} &=& x^2-y\\
&=& 0
\end{eqnarray}
より、
$$y=x^2\tag{1-2}\label{p3478eq1-2}$$
これを\eqref{p3478eq1-1}に戻すと、
$$(t-x)^2=0$$
すなわち、\eqref{p3478eq1-2}は $x=t$ で\eqref{p3478eq1-1}に接する包絡線となっている。
よって、求める範囲は
$$y\le x^2$$
解法2（中級裏技）：平方完成を用いる方法
知ってしまえばなんてことは無いですが、平方完成をこのような用途で使う発想に感動します。しかし残念なことにこの解法は $t$ が二次式のときにしか使えません。
解
\begin{eqnarray}
y &=& -t^2+2xt\\
&=& -(t-x)^2+x^2\tag{2-1}\label{p3478eq2-1}
\end{eqnarray}
一方、この直線と
$$y=x^2\tag{2-2}\label{p3478eq2-2}$$
との交点は、\eqref{p3478eq2-1}, \eqref{p3478eq2-2}から $y$ を消去した式
$$(t-x)^2=0$$
より、$x=t$ で重解を持つことが分かる。
すなわち、\eqref{p3478eq2-1}は $x=t$ で\eqref{p3478eq2-2}に接する包絡線となっている。
よって、求める範囲は
$$y\le x^2$$
解法3（上級裏技）：微分を用いる方法
証明は後ほど示しますが、高校範囲を超えるのでこの解法は学校ではおそらく教えません。しかし、知っていることに罪は無いので使っても一向にかまいません。
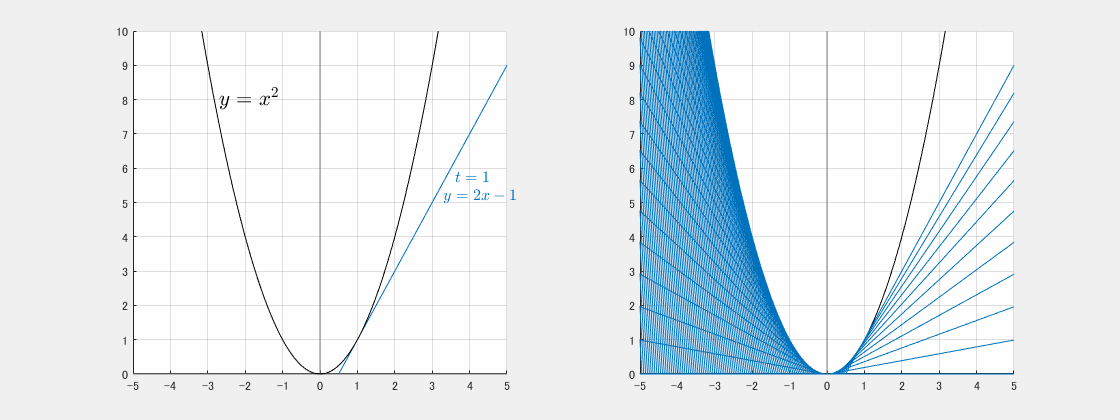
$y=2tx-t^2$ の包絡線の方程式は
- $y=2tx-t^2$ そのもの
- $y=2tx-t^2$ を $t$ で偏微分（偏微分：$x$, $y$ を定数と見なして $t$ で微分）したもの
から $t$ を消去することで得られる。
実は、下側の $t$ で偏微分したものが接点の座標を表しています。
解
$y=2tx-t^2\tag{3-1}\label{p3478eq3-1}$ は $y=x^2\tag{3-2}\label{p3478eq3-2}$ の点 $(t,t^2)$ における接線である。
実際、\eqref{p3478eq3-2}を $x$ で微分すると
$$y^\prime = 2x$$
なので、点 $(t,t^2)$ における接線の方程式は
\begin{eqnarray}
y &=& 2t(x-t)+t^2\\
&=& 2tx-t^2
\end{eqnarray}
となり、\eqref{p3478eq3-1}となっている。
すなわち、\eqref{p3478eq3-1}は $x=t$ で\eqref{p3478eq3-2}に接する包絡線となっている。
よって、求める範囲は
$$y\le x^2$$
解説
どのようにして $y=x^2$ を得たか？
$y=2tx-t^2$ を $t$ で偏微分します。このとき、$x$ や $y$ は定数と見なして微分します。すると、
$$0=2x-2t$$
となり、
$$t=x\tag{3-3}\label{p3478eq3-3}$$
を得ます。これを元の式 $y=2tx-t^2$ に戻すことにより、
\begin{eqnarray}
y &=& 2xx-x^2\\
&=& x^2
\end{eqnarray}
を得ます。\eqref{p3478eq3-3}の $x=t$ は接点の $x$ 座標を表しています。
なお、答案にはこの過程を書く必要はありません。いきなり解のように書けばよいです。
$y=2tx-t^2$ の通過領域：$t$ の範囲が限定されているとき
包絡線解法の利点はこの例のように $t$ の範囲が限定されているときです。【通過領域：順像法】の解法で各自解いて比べてみてください。
$t$ が $0\le t\le 1$ を動くとき、直線 $y=2tx-t^2$ が通過する領域を図示せよ。
アニメーションで確認します。
ここでは、初級解法を例にして解答します。
解
直線の式を $t$ で整理して
$$t^2-2xt+y=0\tag{4-1}\label{p3478eq4-1}$$
これを $t$ に関する二次方程式とみてその判別式を $D$ と置くと、
\begin{eqnarray}
\frac{D}{4} &=& x^2-y\\
&=& 0
\end{eqnarray}
より、
$$y=x^2\tag{4-2}\label{p3478eq4-2}$$
これを\eqref{p3478eq4-1}に戻すと、
$$(t-x)^2=0$$
すなわち、\eqref{p3478eq4-2}は $x=t$ で\eqref{p3478eq4-1}に接する包絡線となっている。
ここで、$t$は
$$0\le t\le 1$$
の範囲を動くから、
求める範囲は図のようになる。ただし、境界を含む。
$y=3t^2x-2t^3\; 0\le t\le 1$ の通過領域
これもまずはアニメーションで確認します。これも、練習問題として【通過領域：順像法】の解法でも各自解いてみてください。
包絡線の解法では、初級解法と中級解法は $t$ の二次式限定版なのでこの問題は解けません。上級解法で解きます。
解
$y=3t^2x-2t^3\tag{5-1}\label{p3478eq5-1}$ は $y=x^3\tag{5-2}\label{p3478eq5-2}$ の点 $(t,t^3)$ における接線である。
実際、\eqref{p3478eq5-2}を $x$ で微分すると
$$y^\prime = 3x^2$$
なので、点 $(t,t^3)$ における接線の方程式は
\begin{eqnarray}
y &=& 3t^2(x-t)+t^3\\
&=& 3t^2x-2t^3
\end{eqnarray}
となり、\eqref{p3478eq5-1}となっている。
すなわち、\eqref{p3478eq5-1}は $x=t$ で\eqref{p3478eq5-2}に接する包絡線となっている。
ここで、$t$は
$$0\le t\le 1$$
の範囲を動くから、
求める範囲は図のようになる。ただし、境界を含む。
解説
どのようにして $y=x^3$ を得たか？
$y=3t^2x-2t^3$ を $t$ で偏微分します。このとき、$x$ や $y$ は定数と見なして微分します。すると、
$$0=6xt-6t^2$$
となり、$6t(x-t)=0$ より
$$t=0,x\tag{5-3}\label{p3478eq5-3}$$
を得ます。これを元の式 $y=3t^2x-2t^3$ に戻しますが、$t=0$ を戻すと $y=0$ です。
$t=x$ を戻すと、
\begin{eqnarray}
y &=& 2xx-x^2\\
&=& x^3
\end{eqnarray}
を得ます。\eqref{p3478eq5-3}の $x=t$ は接点の $x$ 座標を表しています。
また、$t=0$, $y=0$ は $t=x$, $y=x^3$ に含まれているので、$t=x$, $y=x^3$ だけ取り上げれば十分です。
なお、答案にはこの過程を書く必要はありません。いきなり解のように書けばよいです。
上級裏技解法の証明
雰囲気だけつかむ
ではここで、上級裏技の解法でなぜうまくいくのかを説明します。厳密な証明は大学の数学科に任せるとして、ここでは「確かにうまくいくんだな」と何となく雰囲気だけつかむことにします。今一度、証明したい内容を再掲します。
$y=2tx-t^2$ の包絡線の方程式は
- $y=2tx-t^2$ そのもの
- $y=2tx-t^2$ を $t$ で偏微分したもの
から $t$ を消去することで得られる。
求めたいゴールの再確認
直線 $y=2tx-t^2$ と求めたい包絡線との接点を
$$(x,y)$$
と置くと、この $(x,y)$ の満たす関係式を求めることがゴールです。
$(x,y)$ は当然、上の式を満たす
点 $(x,y)$ は $y=2tx-t^2$ 上の点なので、当然ながら $y=2tx-t^2$ に代入して成り立ちます。
$y=2tx-t^2$ に包絡線の条件を組み込むと、下の式となる
包絡線の条件とは何でしょうか。それは一言でいえば、
直線 $y=2tx-t^2$ と接する
ということです。「当たり前やん！それが包絡線でしょ！！」という突っ込みはごもっともです。これをかみ砕くと、点 $(x,y)$ が包絡線との接点なら、$t$ を少し動かして得られる新たな接点 $(x+\Delta x, y+\Delta y)$ までの移動方向
$(\Delta x, \Delta y)$
は包絡線の接線方向である、ということです。すなわち
直線の法線 $(2t,-1)$ と垂直である
ということです。後のためにこの条件を式で表現すると、
$$2t\,\Delta x -1\,\Delta y=0$$
です。$(2t,-1)$ と $(\Delta x,\Delta y)$ が垂直なので、内積を取ってゼロです。ここでこの後の式変形のために両辺を $\Delta t$ で割り、さらに $\Delta x$ を $dx$、$\Delta y$ を $dy$、$\Delta t$ を $dt$ と表記を変えておくと、
$$2t\frac{dx}{dt} -\frac{dy}{dt}=0\tag{6}\label{p3478eq6}$$
です。
このように、微小な変化を大雑把にとらえる感覚は意外と重要です。この感覚の基礎は↓の記事ですので、合わせて確認してもらえると嬉しいです。
さてここで、これを用いるための式変形をします。直線の式
$$y=2tx-t^2$$
を $t$ で全微分します。ここが高校の範囲外なので、これ以下は雰囲気だけつかんでもらえればよいです。直線の式を $2tx-y-t^2=0$ と整理し $t$ で全微分すると次のようになります。
$$2t\frac{dx}{dt}+2x -\frac{dy}{dt}-2t=0$$
ここで、$2t\displaystyle\frac{dx}{dt}-\displaystyle\frac{dy}{dt}$ は\eqref{p3478eq6}よりゼロです。よってこの式は
$$2x-2t=0$$
となりますが、これは直線の式 $y=2tx-t^2$ を $t$ で偏微分（偏微分：$x$, $y$ を定数と見なして $t$ で微分）したものにほかなりません。
つまり
つまり、
点 $(x,y)$ が包絡線との接点の座標なら $2x-2t=0$ を満たす
ということであり、また
点 $(x,y)$ が包絡線との接点の座標なら元の直線の式 $y=2tx-t^2$ を満たす
でもあるわけなので、この2つから $t$ を消去すれば包絡線の軌跡となります。
まとめ
領域問題を包絡線の解法で解きました。この解法は楽に解けますが少しトリッキーでもあります。従って、まずは基本形である【通過領域：順像法】【通過領域：逆像法】をしっかりとできるようになり、余裕があればこの解法をマスターするようにしましょう。この解法を知っていれば見通しは良くなるので、余裕のある人はさらなるレベルアップを狙えます。
コメント