【放物線の1/3公式と1/12公式】1/6公式だけではない 裏技の時短公式！ でも、覚えるより導出を

　1/6公式は比較的有名ですが、近しいものに1/3公式と1/12公式があります。これらも使えればかなりの時短になるため、経験しておくとよいと思います。しかし覚えるほど頻繁には出てこないので、そんな公式があるな、くらいの認識で大丈夫です。要は必要になれば自分で導出すればよいのですから。

ここでは公式の導出を行います。自分で楽に導出ができるように、式変形のポイントをアニメーションでイメージ付けします。

この公式のうま味は解と係数の関係を用いることです。使い方は↓の記事と共通なのでこちらを見てください。

1/3公式

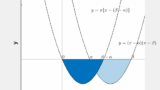
それは、放物線と直線が接する場合の面積　

　下の図↓のように放物線と直線が接していて、接点を端点とする面積 $S$ は次のようになります。

証明

式変形のイメージ

　面積を求めるので、上の線である放物線から下の線である直線を引いて $\alpha$ から $\beta$ まで積分します。

証明

$$\begin{eqnarray} S &=& \int_\alpha^\beta \{(x^2+bx+c)-(px+q)\}\,dx\\ &=& \int_\alpha^\beta (x-\alpha)^2\,dx\\ &=& \left[\frac{1}{3}(x-\alpha)^3\right]_\alpha^\beta\\ &=& \frac{1}{3}(\beta-\alpha)^3 \end{eqnarray}$$

1/12公式

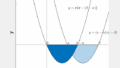
それは、2つの放物線と直線が接する場合の面積

　下の図↓のように2つの放物線と直線が接していて、接点を端点とする面積 $S$ は次のようになります。ただし、2つの放物線の二次の係数は同じでなくてはなりません。

証明

式変形のイメージ

　面積を求めるので、上の線である放物線から下の線である直線を引いて $\alpha$ から $\beta$ まで積分します。ただし、その間に放物線が2つあるので、積分を切り替える必要があります。切り替えるポイントは、対称性から $\alpha$ と $\beta$ の中点です。

証明

$$\begin{eqnarray} S &=& \int_\alpha^\frac{\alpha+\beta}{2} \{(x^2+b_1x+c_1)-(px+q)\}\,dx\\ && +\int_\frac{\alpha+\beta}{2}^\beta \{(x^2+b_2x+c_2)-(px+q)\}\,dx\\ &=& \int_\alpha^\frac{\alpha+\beta}{2} (x-\alpha)^2\,dx + \int_\frac{\alpha+\beta}{2}^\beta (x-\beta)^2\,dx\\ &=& \left[\frac{1}{3}(x-\alpha)^3\right]_\alpha^\frac{\alpha+\beta}{2} + \left[\frac{1}{3}(x-\beta)^3\right]_\frac{\alpha+\beta}{2}^\beta\\ &=& \frac{1}{12}(\beta-\alpha)^3 \end{eqnarray}$$

まとめ

　この手の公式はそんなに頻繁に出てくるわけではないので覚えるだけのコスパは良くないと思います。しかし一方で知っていればかなりの時短にはなるため、公式自体を覚えるのではなく、ここで示したようなアニメーションをイメージできるようにしておき、

確か簡単な式になるな

という感覚を持っておくとよいです。そうすれば計算をする気になりますし、あるいはここに示したように公式を導出してから問題に取り掛かることもできます。

解と係数の関係を用いたうまい使い方は↓の記事を見てください。1/3公式や1/12公式にも応用できます。