ここでは次のような積分をかっこのままで行うことを目的にします。かっこのままで行うので置換積分とは言い難いかもしれないですが、置換積分を暗算しているにすぎません。
$$\int(2x-1)^2\, dx$$
$$\int\sin x\,\cos x\,dx$$
かっこのままで積分する
これは、合成関数の微分↓の逆演算です。
$\left((2x-1)^3\right)^{\prime} = 3(2x-1)^2\cdot 2$
$\left(\sin^2 x\right)^{\prime} = 2\sin x\cdot\cos x$
です。これを巻き戻すイメージです。
$\int(2x-1)^2\, dx$
解
$\left((2x-1)^3\right)^{\prime} = 3(2x-1)^2\cdot 2$ より、
$$(2x-1)^2 = \frac{1}{2}\frac{1}{3}\left((2x-1)^3\right)^{\prime}$$
$$\therefore\;\int(2x-1)^2\, dx = \frac{1}{6}(2x-1)^3 + C$$
不定積分の場合、積分定数 $C$ を忘れずにつけるようにしましょう。
$\int\sin x\,\cos x\,dx$
解
$\left(\sin^2 x\right)^{\prime} = 2\sin x\cdot\cos x$ より、
$$\sin x\cos x = \frac{1}{2}\left(\sin^2 x\right)^{\prime}$$
$$\therefore\;\int\sin x\,\cos x\,dx = \frac{1}{2}\sin^2 x + C$$
置換して積分する
適当な $g(x)$ を選び、$t=g(x)$ と置換します。この置換のイメージは、【置換積分#2】なぜ置換するとうまく積分できるのかで述べていますので、ここでは上記の「かっこのままで積分する」を暗算しているに過ぎないということを理解するだけにします。
$\int(2x-1)^2\, dx$
$t=2x-1$ とおくと、
- $(2x-1)^2 = t^2$
- $dt = 2dx$
であるから、
\begin{eqnarray}
\int(2x-1)^2\,dx &=& \int t^2\cdot\frac{1}{2}dt\\
&=& \frac{1}{2}\frac{1}{3}t^3 + C\\
&=& \frac{1}{6}(2x-1)^3 + C
\end{eqnarray}
となり、先の結果と一致しますし、途中の式はまさに「かっこのままで積分する」場合の暗算になっています。
$\int\sin x\,\cos x\,dx$
同様に、$t=\sin x$ とおくと、
- $\sin x\,\cos x = t\cos x$
- $dt = \cos x\, dx$
であるから、
\begin{eqnarray}
\int\sin x\,\cos x\,dx &=& \int t\, dt\\
&=& \frac{1}{2}t^2 + C\\
&=& \frac{1}{2}\sin^2 x + C
\end{eqnarray}
です。$t=\sin x$ と置換しても $t\cos x$ となって $x$ が残ってしまうところが不安になりますが、その次の $dt=\cos x\, dx$ で不安の種だった $\cos x$ がうまく消えてくれます。この不安も、$\sin^2 x$ を微分した際に $\cos x$ が出てくることを思い出せば後に消えてくれることが想像されるため、解消されます。結局、暗算の力が不安を解消してくれています。
ここまでのところで凡そつかめた方は、より本質的なこちらの記事をご覧くださいませ。
もう少し例題を踏まえたい方は続きをご覧ください。
例題: かっこのままで
$\int x(x^2-1)\, dx$
$〇^2$ を微分すると $〇$ の項が出てくることと、$x^2-1$ を微分すると $x$ の項が出てくることに着目すると、$(x^2-1)^2$ を微分してみようかと動機付けされます。
解
$\left((x^2-1)^2\right)^{\prime} = 2(x^2-1)\times 2x$ より、
$$x(x^2-1) = \frac{1}{4}\left((x^2-1)^2\right)^{\prime}$$
$$\therefore\; \int x(x^2-1)\, dx = \frac{1}{4}(x^2-1)^2+C$$
確認
一瞬、答えが違うように見えてしまいますが、よくよく見ると同じです。定数項に騙されています。
$\int\displaystyle\frac{x}{\sqrt{1-x^2}}\, dx$
$\sqrt{〇}$ を微分すると $\displaystyle\frac{1}{\sqrt{〇}}$ の項が出てくることと、$1-x^2$ を微分すると $x$ の項が出てくることに着目すると、$\sqrt{1-x^2}$ を微分してみようかと動機づけされます。
解
$\left(\sqrt{1-x^2}\right)^{\prime} = \displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{\sqrt{1-x^2}}\times (-2x)$ より、
$$\frac{x}{\sqrt{1-x^2}}=-\left(\sqrt{1-x^2}\right)^{\prime}$$
$$\therefore\;\int\frac{x}{\sqrt{1-x^2}}\, dx = -\sqrt{1-x^2}+C$$
確認
$\int\displaystyle\frac{x}{x^2+1}\, dx$
$\log{〇}$ を微分すると $\displaystyle\frac{1}{〇}$ の項が出てくることと、$x^2+1$ を微分すると $x$ の項が出てくることに着目すると、$\log{(x^2+1)}$ を微分してみようかと動機付けされます。
解
$\left(\log{(x^2+1)}\right)^{\prime}=\displaystyle\frac{1}{x^2+1}\times 2x$ より、
$$\frac{x}{x^2+1} = \frac{1}{2}\left(\log{(x^2+1)}\right)^{\prime}$$
$$\therefore\;\int\frac{x}{x^2+1}\, dx = \frac{1}{2}\log{(x^2+1)}+C$$
確認
$\int\displaystyle\frac{\log{x}}{x}\, dx$
$〇^2$ を微分すると $〇$ の項が出てくることと、$\log{x}$ を微分すると $\displaystyle\frac{1}{x}$ の項が出てくることに着目すると、$(\log{x})^2$ を微分してみようかと動機付けされます。
解
$\left((\log{x})^2\right)^{\prime} = 2\log{x}\times\displaystyle\frac{1}{x}$ より、
$$\frac{\log{x}}{x} = \frac{1}{2}\left((\log{x})^2\right)^{\prime}$$
$$\therefore\;\int\frac{\log{x}}{x}\, dx = \frac{(\log{x})^2}{2}+C$$
確認
$\int xe^{x^2}\,dx$
$e^{〇}$ を微分しても $e^{〇}$ の項が残ることと、$x^2$ を微分すると $x$ の項が出てくることに着目すると、$e^{x^2}$ を微分してみようかと動機付けされます。
解
$\displaystyle\left(e^{x^2}\right)^{\prime} = 2xe^{x^2}$ より、
$$xe^{x^2} = \frac{1}{2}\left(e^{x^2}\right)^{\prime}$$
$$\therefore;\int xe^{x^2}\, dx=\frac{1}{2}e^{x^2}+C$$
確認
$\int x(x-2)^4\,dx$
$0$ を足すことでうまくいきます。
解
\begin{eqnarray}
x(x-2)^4 &=& (x-2+2)(x-2)^4\\
&=& (x-2)^5+2(x-2)^4
\end{eqnarray}
より、
\begin{eqnarray}
&&\int x(x-2)^4\, dx\\
&&\qquad = \int \left\{(x-2)^5+2(x-2)^4\right\}\, dx\\
&&\qquad = \frac{1}{6}(x-2)^6+\frac{2}{5}(x-2)^5+C
\end{eqnarray}
確認
$\int\sqrt{x+1}\,(x+2)\, dx$
これも先ほどと同様です。今度は $2$ を $1+1$ に分けます。
解
\begin{eqnarray}
\sqrt{x+1}\,(x+2) &=& \sqrt{x+1}\,(x+1+1)\\
&=& (x+1)^\frac{3}{2}+(x+1)^\frac{1}{2}
\end{eqnarray}
より、
\begin{eqnarray}
&&\int\sqrt{x+1}\,(x+2)\, dx\\
&&\qquad = \int\left\{(x+1)^\frac{3}{2}+(x+1)^\frac{1}{2}\right\}\, dx\\
&&\qquad = \frac{2}{5}(x+1)^\frac{5}{2}+\frac{2}{3}(x+1)^\frac{3}{2}+C
\end{eqnarray}
確認
まとめ
以上のように、合成関数の微分を逆再生することでかっこのままで積分することができます。
従って、かっこのままで積分することができるようになるためには、合成関数の微分の練習をしっかり行うことが必要です。それも、できるだけシンプルに解けるように。シンプルな解き方は冒頭で紹介した↓の記事の中で「かっこのままで微分」として述べていますので、ぜひ参考にしてください。
目次で「例1：$y=(2x-1)^2$の微分 かっこのままで微分する」まで進んでください。もしくは直接該当箇所へはこちら。
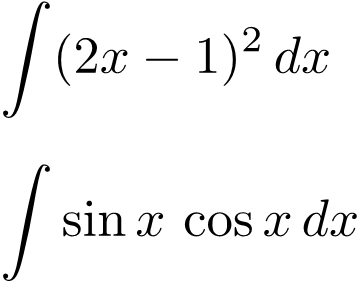
コメント