【外接円の半径】円周角の定理と相似で求める 高校入試対策

　高校入試数学で頻出する『三角形の外接円の半径を求める問題』。円周角の定理や相似の利用、三平方の定理を組み合わせることで、複雑に見える問題もスッキリ解けます。本記事では、外接円の半径を求める解法の流れと入試で役立つポイントを徹底解説します。

解きたい問題と解くための基本事項

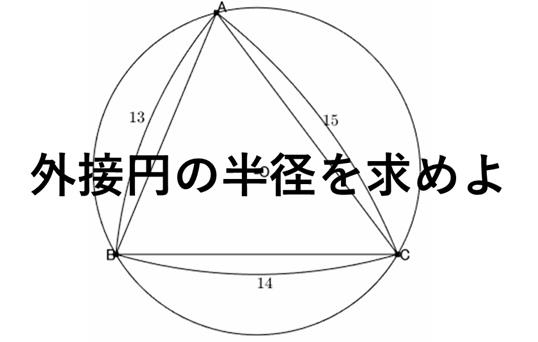
問題

　解き方が想像つく人は「解きたい問題の解答」章に行ってください。ここでは、この問題を解く発想を基本問題から確認していきます。

基本その1：相似で解く（円周角の定理の利用に気づく必要あり）

一気通貫アニメーション

解説

　実は色のついている三角形二つは相似です。どちらも直角三角形です。$\triangle\mathrm{ABH}$ は $\mathrm{H}$ を直角になるようにとったので良いとして、$\triangle\mathrm{ADC}$ は、$\mathrm{AD}$ が直径なので、円周角の定理より $\angle\mathrm{ACD}=90^\circ$ です。

　そしてさらにもう一つ、これも円周角の定理により、

$$\angle\mathrm{ABH}=\angle\mathrm{ADC}$$

です。
これは、どちらも同じ弧 $\stackrel{\huge\frown}{\mathrm{AC}}$ に対する円周角なので、同じです。

2角が等しいので、相似です。

$$\triangle\mathrm{ABH}\unicode[sans-serif]{x223D}\triangle\mathrm{ADC}$$

実際、下記のアニメーションで $\triangle\mathrm{ABH}$ を回転させて $\triangle\mathrm{ADC}$ に重ねれば相似であることは直感的にも理解できます。

そして比例式を立てれば、

$$13:\mathrm{AD}=12:15$$

なので、

$$\mathrm{AD}=\frac{13\times\cancel{15}\,5}{\cancel{12}\,4}=\frac{65}{4}$$

です。$\mathrm{AD}$ は直径であり、$2r$ なので、

$$r=\frac{65}{8}$$

です。

基本その2：三平方の定理で直角三角形に分割する

一気通貫アニメーション

解説

三辺が分かっているときの高さの求め方はこうだ！

　まずは点 $\mathrm{A}$ から辺 $\mathrm{BC}$ に垂線を下ろします。

直角三角形が二つできますので、底辺の長さを文字で置きます。$\mathrm{BH}=x$ と置けば、$\mathrm{HC}=14-x$ です。

ここで、二つの直角三角形それぞれに三平方の定理を適用します。$\mathrm{AH}$ を介して二つ式を立てます。

これを $x$ について解けば、$x=5$ と求まります。

下記の記事も併せて読むと幅が広がります。

解答

問題再掲

　以上で解答するための基礎知識は養えたので、解答していきます。再度問題を思い出します。

一気通貫アニメーション

解説

基本その1により、直角三角形を得る

　基本その1により、下記の直角三角形を得ます。

直径を斜辺とする直角三角形を作る

　直径を斜辺とし、点 $\mathrm{C}$ を対角とする直角三角形を作ります。

基本形その1により、半径が分かる

　基本形その1により $\triangle\mathrm{ABH}\unicode[sans-serif]{x223D}\triangle\mathrm{ADC}$ です。

相似の比例式を立て、

$$13:2r=12:15$$

から、

$$r=\frac{65}{8}$$

を得ます。

まとめ

　三角形の外接円の半径を求めました。この求め方の中には、三辺が既知の場合の高さの求め方があり、また円周角があり、そして相似がありで複合的です。この問題は誘導があって出てくるのであって、一から全てを自分で構成して外接円の半径を求めさせる問題は難しすぎてあまり出ないと思いますが、自分で構成して求められるようになっておけば、誘導問題も楽になりますし、他の問題でも発想が応用できたりします。