微分の代表的な応用のひとつが「接線の方程式」です。
「微分で接線を求める」と聞くと難しく感じますが、実は考え方は3パターンに整理できます。
本記事では、次の3つの状況を順に扱いながら、接線の求め方を体系的に整理していきます。
- 接点の座標が分かっている場合
- 接点が分からない場合
- 曲線外の点から接線を引く場合
曲線上の点から接線を引く:接点既知
$y=x^3-2x-2$ 上の点で、接点の座標が $x=1$ のとき、その接線の方程式ともう一つの交点の座標を求めよ。
直線の方程式は、傾きと通る点が分かれば求まります。
傾きは微分で求め、通る点は $x=1$ を代入すれば分かります。
傾きは微分で求める
元の関数
$$f(x)=x^3-2x-2$$
を微分すると、
$$f^\prime(x)=3x^2-2$$
よって、
$$f^\prime(1)=1$$

通る点は $x=1$ を代入して $y=-3$
$$f(1)=1^3-2\cdot 1-2=-3$$
接線の方程式
傾きと通る点が出たので、直線の方程式はすぐに出ます。
\begin{eqnarray}
y &=& 1(x-1)-3\\
&=& x-4
\end{eqnarray}
接線の方程式:$y=x-4$
あえて $y=1(x-1)-3$ と書いています。直線の式のコツです(下記記事)。

もう一つの交点
曲線と接線を連立すると、
\begin{eqnarray}
\left\{ \begin{array}{l}
y=x^3-2x-2 \\
y=x-4\tag{1}\label{p306eq1}
\end{array}
\right.
\end{eqnarray}
より、
$$x^3-3x+2=0$$
ここで次のことに着目します。
$x=1$ で接している $\Leftrightarrow$ $(x-1)^2$ を因数に持つ
つまり、
$$(x-1)^2(x-□)=0$$
の形になるはず。元の式:
$$x^3-3x+2=0$$
と見比べて、半ば強引に、
$$(x-1)^2(x+2)=0$$
と分かります。(定数項を見比べれば分かりますね。一応、展開して検算しましょう。)
もう一つの交点は、$x=-2$。\eqref{p306eq1}より $y=-6$ も分かります。
もう一つの交点:$(-2,-6)$
曲線上の点から接線を引く:接点未知
$y=x^3-2x-2$ において、傾きが $1$ である接線の方程式を求めよ。
これは直前の問題と酷似しているので、接線の1本はすぐに分かります。
そう、$y=x-4$ です。
しかしここでは、直前の問題がないとして2つの方法で解いていきます。
- 接点が彷徨うイメージ
- 直線が彷徨うイメージ
方法1:接点が彷徨う
接点が彷徨って、傾きが $1$ になったところで「ここだ!」という感じです。
そして、その「ここだ!」は実は 2か所 あります。
では、その “傾き $1$ の場所” をどう探すかというと $—$
ポイントは 微分 です。
接点を彷徨わせるには、まず微分して、導関数(下の赤い線)を見ます。
これが「各 $x$ での傾き」を表しています。
微分すると、
$$y^\prime = 3x^2-2$$
この値が $1$ になる $x$ を求めればよく、
$$3x^2-2=1$$
$$3(x-1)(x+1)=0$$
よって、
$$x=-1,\, 1$$
の2か所で「ここだ!」が現れます。
一つ目の「ここだ!」
接線が彷徨って傾き $1$ を探しています。
赤のグラフは青の傾きの値です。
$x=-1$ のとき、青の傾きが $1$ になります。
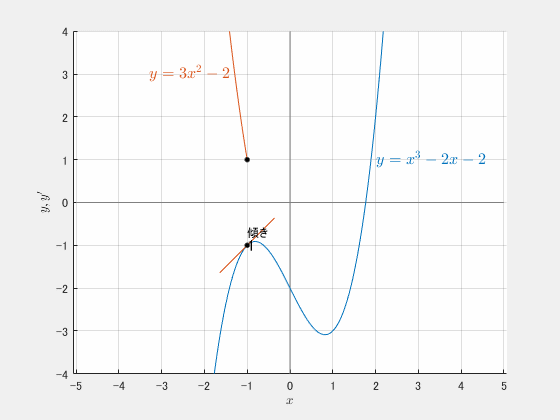
接点の座標は $(-1,-1)$。
このときの接線の方程式は、
\begin{eqnarray}
y &=& 1(x+1)-1\\
&=& x
\end{eqnarray}
二つ目の「ここだ!」
さらに彷徨って傾き $1$ を探すと、もう一つ見つかります。
$x=1$ のときも、青の傾きは $1$ になります。
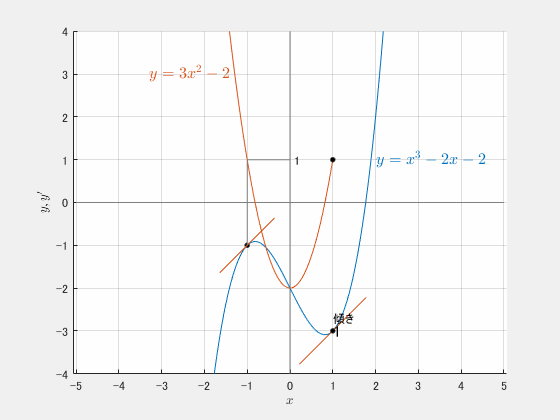
接点の座標は $(1,-3)$。
このときの接線の方程式は、
\begin{eqnarray}
y &=& 1(x-1)-3\\
&=& x-4
\end{eqnarray}
接線の方程式
求める接線の方程式は、
\begin{eqnarray}
y&=&x\\
y&=&x-4
\end{eqnarray}
方法2:直線が彷徨う
傾き $1$ の直線が彷徨って、曲線に接したところで「ここだ!」という感じです。
そして、その「ここだ!」は 2か所 あります。
では、直線をどう彷徨わせるかというと $—$
ポイントは、
傾き $1$ の直線を $y=x+a$ と置き、$a$ を動かす
という発想です。
この直線が曲線に接するということは、
連立方程式が重解を持つ
ということです。
連立方程式を立てる
まずは素直に連立します。
\begin{eqnarray}
\left\{ \begin{array}{l}
y=x^3-2x-2 \\
y=x+a
\end{array}
\right.
\end{eqnarray}
これが重解を持てばよいのですが、
このままでは少し扱いにくいので、見方を変える工夫 をします。
連立方程式の見方を変える
上記の連立方程式の解 $x$ は、次の連立方程式の解 $x$ と同じです。
\begin{eqnarray}
\left\{ \begin{array}{l}
y=x^3-3x-2 \\
y=a
\end{array}
\right.
\end{eqnarray}
こう見ると、
$y=x^3-3x-2$ のグラフと、水平線 $y=a$ の交点
という形になり、状況が一気に分かりやすくなります。

この図より、
- $a=0$
- $a=-4$
のとき、水平線が曲線に接している(=重解を持つ)ことが分かります。
接線の方程式
接線の方程式は $y=x+a$ と置いていたので、
求める接線の方程式は、
\begin{eqnarray}
y&=&x\\
y&=&x-4
\end{eqnarray}
となります。
連立方程式の見方を変える発想は下記の記事で取り扱っています。
曲線外の点から接線を引く
$y=x^3-2x-2$ の接線が点 $(1,1)$ を通るとき、接線の方程式を求めよ。
外部点から接線を引く典型問題です。
接線が彷徨って、点 $(1,1)$ を通ったところで「ここだ!」という感じです。
そして、その「ここだ!」は 1か所だけ です。
では、どう彷徨わせるかというと $—$
ポイントは、
接点を $x=a$ と置き、その点での接線の式を立てる
という発想です。
その接線が点 $(1,1)$ を通るということは、
接線の式に $(1,1)$ を代入して成り立つ
ということです。
接点を設定して接線の方程式を立てる
直線の方程式は、傾きと通る点が分かれば書けます。
傾き
微分すると、
$$f^\prime(x) = 3x^2-2$$
よって、接点 $x=a$ における傾きは、
$$f^\prime(a) = 3a^2-2$$
通る点
接点の座標は、
$$f(a)=a^3-2a-2$$
接線の方程式
傾きと通る点が分かったので、接線の方程式は
$$y = (3a^2-2)(x-a)+a^3-2a-2\tag{2}\label{p306eq2}$$
となります。
接線が点 $(1,1)$ を通る
では、この接線が点 $(1,1)$ を通る条件を立てます。
\begin{gather}
1=(3a^2-2)(1-a)+a^3-2a-2\\
2a^3-3a^2+5=0\\
(a+1)(2a^2-5a+5)=0
\end{gather}
一つの解は、$a+1=0$
$$a+1=0 \Rightarrow a=-1$$
もう一つの解は、$2a^2-5a+5=0$
判別式を計算すると、
$$D=5^2-4\cdot 2\cdot 5=25-40<0$$
よって実数解なし。
接線の方程式
意味を持つのは $a=-1$ のときだけです。
接線のは \eqref{p306eq2} の、
$$y = (3a^2-2)(x-a)+a^3-2a-2$$
に $a=-1$ を代入して、
$$y=x$$
となります。
まとめ
接線の方程式は、状況によってアプローチが変わりますが、
本質はどれも 「傾き(導関数)と通る点」 の2つです。
- 接点が分かっているとき
→ 微分して傾きを出し、通る点を代入するだけ。 - 接点が分からないとき(接点が彷徨う)
→ 導関数を見て「傾きが1になる場所」を探す。
つまり、導関数の値=接線の傾き。 - 接点が分からないとき(直線が彷徨う)
→ 直線を $y=x+a$ などといったパラメータで置き、
パラメータを避けた連立方程式で接する場所を探す。 - 外部点から接線を引くとき
→ 接点を (a) と置き、接線の式に外部点を代入して条件式を作る。
どの方法も、
「接するとはどういうことか?」
というイメージを持つと一気に理解が深まります。
今回の記事では、
- 接点が動く
- 直線が動く
- 外部点から接線を引く
という3つの“彷徨う”イメージを通して、
接線の方程式の考え方を体系的に整理しました。
接線は、微分の中でも特に“イメージ”が大事なテーマです。
ぜひ、図や動画を見ながら「ここだ!」の感覚をつかんでみてください。





コメント