複素数の逆数 $\displaystyle\frac{1}{z}$ は、単なる計算上の操作ではなく、複素数平面においておもしろい幾何変換になっています。これを理解すると、複素数の問題の見通しが一気によくなります。
本記事では、アニメーションと図形的アプローチを中心に、「直線 → 円」「円 → 円」へと変換される逆数の性質を統一的に理解します。計算よりもまずイメージをつかむことを大切にしています。
逆数 $\displaystyle\frac{1}{z}$ の基本イメージ
複素数 $z$ の逆数 $\displaystyle\frac1z$ は次のように定義されます。
$$z\cdot\frac{1}{z}=1$$
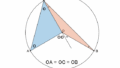
図形的には、青い点 $z$ に対して赤い点 $\displaystyle\frac{1}{z}$ は次の性質をもちます。
・長さは逆数になる($|z|=3$ なら $|1/z|=1/3$)
・角度は $x$ 軸に関して対称になる(共役と同じ)

単位円を描いているのは、単位円の外側の点は逆数を取ると単位円の内側に移ることを強調するためです。
$z$ が単位円上にあるときは、当然 $\displaystyle\frac{1}{z}$ も単位円上にあります。

さらに、$z$ が下図の灰色の円上を動くとき、$\displaystyle\frac{1}{z}$ は驚くべきことに $x=1$ の直線上 を動きます。

これは 2025 年度の東大で出題された内容です。(解説はこちら)
直線はどう変換されるか
アニメーションで理解する
まずはイメージをつかみましょう。
青い直線を動かしても、逆数である赤い線は常に「円」を描きます。
しかもその円は必ず 原点を通る円 になります。
直線が原点に近づくほど、赤い円は大きくなり、直線が原点を通る瞬間だけ、赤い軌跡は直線になります。



式で理解する
図形的にイメージできたら、式でも確認してみましょう。直線は複素数 $a$ を用いて次のように表せます。
$$|z|=|z-a|$$
これは原点と点 $a$ の垂直二等分線です。(詳しくはこちら)
逆数変換 $\omega=\displaystyle\frac{1}{z}$ を用いると、$z=\displaystyle\frac{1}{\omega}$ を代入して、
$$\left|\frac{1}{\omega}\right|=\left|\frac{1}{\omega}-a\right|$$
両辺に $\left|\displaystyle\frac{\omega}{a}\right|$ を掛けると、
$$\left|\omega-\frac{1}{a}\right|=\left|\frac{1}{a}\right|$$
これは、
中心 $\displaystyle\frac{1}{a}$、半径 $\displaystyle\left|\frac{1}{a}\right|$ の円
を表します。直線が円に変換される理由が式からも分かります。
原点を通らない円はどう変換されるか
アニメーションで理解する
青い円を動かしても、逆数である赤い線は常に「円」を描きます。
青の円が原点に近づくほど、赤の円は大きくなる。
そして、青の円が原点を通る瞬間だけ、赤の軌跡は直線になります(下図真ん中)。



式で理解する
円は複素数 $a$ と正の数 $r$ を用いて次のように表せます。
$$|z-a|=r$$
逆数変換 $\omega=\displaystyle\frac{1}{z}$ を用いて $z=\displaystyle\frac{1}{\omega}$ を代入すると、
$$\left|\frac{1}{\omega}-a\right|=r$$
両辺に $\left|\displaystyle\frac{\omega}{a}\right|$ を掛けると、
$$\left|\omega-\frac{1}{a}\right|=\frac{r}{|a|}|\omega|$$
つまり、
$$\left|\omega-\frac{1}{a}\right|:|\omega|=\frac{r}{|a|}:1$$
これは、
点 $\displaystyle\frac{1}{a}$ と原点からの距離が一定比 $\left(\displaystyle\frac{r}{|a|}:1\right)$ になる点の集合(=円)
を表します。円は円に変換されることが分かります。
逆数変換は「円円変換」である
ここまでの結果をまとめると、逆数変換 $\displaystyle\frac{1}{z}$ は次のように整理できます。
・直線 → 原点を通る円
・原点を通る円 → 直線
・原点を通らない円 → 原点を通らない円
つまり、逆数変換は「円円変換」です。直線も円の一部とみなせば、すべてが円に変換される統一的な構造が見えてきます。
まとめ
複素数の逆数 $\displaystyle\frac{1}{z}$ が描く軌跡を、アニメーションと式の両面から整理しました。直線も円も、逆数変換によってすべて円に変換されるという統一的な構造が見えてきたと思います。
逆数変換は軌跡問題でも頻出で、2025 年度の東大入試でも登場しました。実戦的な扱いは次の記事で解説しています:
また、直線や円の軌跡の基本的な考え方を整理したい場合は、こちらの記事が参考になります:





コメント