【ベクトル：一次独立、内積】直感的イメージでその意味を完全理解！！

　ベクトルを学習していきなりこのような言葉に見舞われ苦戦しますよね。しかしこの二つ、一次独立と内積は非常に大事な概念なのでここで完全に理解します。一次独立はアニメーションを使ってその意味を理解します。内積は図形的な意味を理解して垂線の足問題などへの発展もできるようにします。

一次独立のイメージ

平面上の任意の点は2つの一次独立なベクトルを定めれば表現できる

　通常私たちが使う座標平面は下図の左のようです。当然ながらこの座標平面を使って、すなわち $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ を使って平面上の任意の点を表現できます。例えば点 $\mathrm{P}$ は $(5,4)$ ですが、これは、

$$\begin{eqnarray} \begin{pmatrix}5\\4\end{pmatrix} &=& 5\begin{pmatrix}1\\0\end{pmatrix}+4\begin{pmatrix}0\\1\end{pmatrix}\\ &=& 5\,\overrightarrow{\mathrm{OA}}+4\,\overrightarrow{\mathrm{OB}} \end{eqnarray}$$

と表現できます。

一方、図の右のように $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ を取ったとしても同様に点 $\mathrm{P}$ を表現できます。このときは、

$$\begin{eqnarray} \begin{pmatrix}5\\4\end{pmatrix} &=& 2\begin{pmatrix}2\\1\end{pmatrix}+1\begin{pmatrix}1\\2\end{pmatrix}\\ &=& 2\,\overrightarrow{\mathrm{OA}}+1\,\overrightarrow{\mathrm{OB}} \end{eqnarray}$$

です。

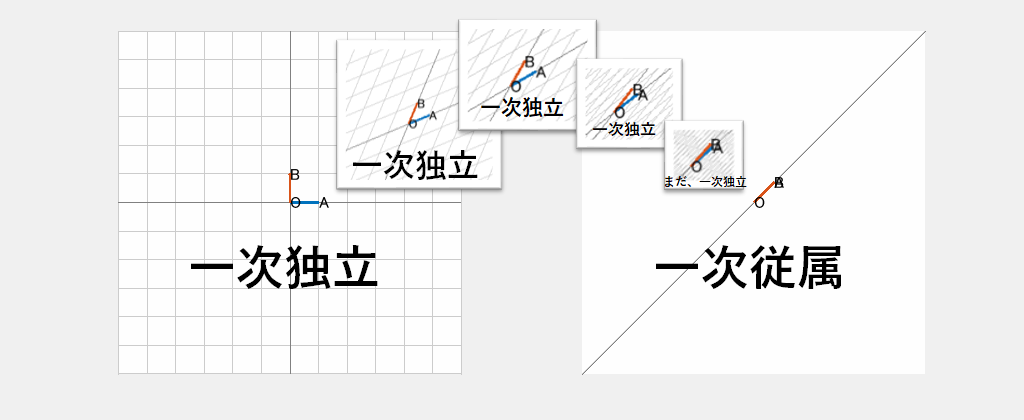
このように基本的には $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ をどのように取っても任意の点を表現することができます。ある条件を除いては。

その、除くべきある条件とは、$\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ が平行になる場合、もしくは少なくともどちらか一方が $\overrightarrow{0}$ となる場合です。この時だけは、表現できる点は直線上の点のみになってしまいます。

そのことを下記でイメージします。これは、$\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ が平行でない間はどんな場合でも座標のメッシュが描かれており、任意の点が表現できることを表しています。一方、最後の瞬間に平行になってしまい、こうなると座標のメッシュが描けず、直線上の点のみしか表現できません。このような状態を、一次独立に対して一次従属と言います。

以上のように、

のです。もちろん、これが空間なら3つのベクトル、ということになります。それに関してはこの記事↓で詳しく扱っています。

内積の図形的意味

$\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}=|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|\cos\theta$

　内積の図形的定義は次のようです。

この式は角度を求める際によく使います。

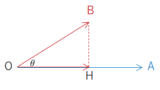
角度問題の例

解

$$\begin{eqnarray} \cos\theta &=& \frac{\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}}{|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|}\\ &=& \frac{\begin{pmatrix}\sqrt{3}\\1\end{pmatrix}\cdot\begin{pmatrix}1\\\sqrt{3}\end{pmatrix}}{\left|\begin{pmatrix}\sqrt{3}\\1\end{pmatrix}\right|\left|\begin{pmatrix}1\\\sqrt{3}\end{pmatrix}\right|}\\ &=& \frac{2\sqrt{3}}{2\times 2}\\ &=& \frac{\sqrt{3}}{2} \end{eqnarray}$$

より、

$$\theta = \frac{\pi}{6}$$

$\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}=|\overrightarrow{\mathrm{OH}}||\overrightarrow{\mathrm{OA}}|$

　また、これをもう少しかみ砕いて次のように解釈できると理解の幅が広がります。

　このように捉えることで、$\theta=90^\circ$ の場合は内積の値が $0$ になることが直感的に理解できますし、また内積の正負の値も直感的に理解できます。

それ以上に役に立つ場面があります。垂線の足問題です。別記事↓にて詳しく解説しています。

まとめ

　一次独立と内積を直感的に理解しました。平面上の任意の点は、一次独立なベクトルを2つ使うことにより表現できます。また角度は内積と結びつけることができます。これらの性質を使い、図形の問題を単なる計算問題に落とし込むことができる、それがベクトルの強みです。