平面への垂線の足

0. 問題

問題のイメージ

関連記事

ここでは、下記の記事と同じ問題を扱いますので、それらを合わせて読むことでより幅の広い理解ができます。

この記事↓は、平面の方程式が与えられている場合で、今回の 2. の解き方に相当します。

この記事↓は、平面の方程式が与えられている場合で、1. も 2. もすっ飛ばして距離だけをより簡単に求める方法です。

準備

平面 $\alpha$ は、2つの一次独立なベクトル $\overrightarrow{\mathrm{AB}}$ と $\overrightarrow{\mathrm{AC}}$ で張られる平面です。$\mathrm{A}(0,0,1)$, $\mathrm{B}(0,1,0)$, $\mathrm{C}(2,0,0)$ から、

\[\overrightarrow{\mathrm{AB}} = \begin{pmatrix}0\\1\\-1\end{pmatrix}\\
\overrightarrow{\mathrm{AC}} = \begin{pmatrix}2\\0\\-1\end{pmatrix}\]

この二つのベクトルを基底ベクトルと呼びます。

後に使うので $\overrightarrow{\mathrm{PA}}$ もここで求めておきます。$\mathrm{P}(-2,-1,0)$ から、

$$\overrightarrow{\mathrm{PA}} = \begin{pmatrix}2\\1\\-1\end{pmatrix}$$

1. 垂直：内積=0

平面上の点の表し方

点 $\mathrm{H}$ は平面 $\alpha$ 上の点なので、

$$\overrightarrow{\mathrm{PH}} = \overrightarrow{\mathrm{PA}}+s\,\overrightarrow{\mathrm{AB}}+t\,\overrightarrow{\mathrm{AC}}\tag{1-1}\label{eq1-1}$$

と書けます。平面上の点をベクトルで表現する方法は下記で詳しく扱っています。

垂直：内積＝0

平面 $\alpha$ に垂直ということは $\alpha$ の基底ベクトル $\overrightarrow{\mathrm{AB}}$, $\overrightarrow{\mathrm{AC}}$ に垂直。すなわち、

• $\overrightarrow{\mathrm{PH}}\perp\overrightarrow{\mathrm{AB}}$
• $\overrightarrow{\mathrm{PH}}\perp\overrightarrow{\mathrm{AC}}$

ということです。

$\overrightarrow{\mathrm{PH}}\perp\overrightarrow{\mathrm{AB}}$

$$\overrightarrow{\mathrm{PH}}\cdot\overrightarrow{\mathrm{AB}}=0$$

より\eqref{eq1-1}を代入して、

$$(\overrightarrow{\mathrm{PA}}+s\,\overrightarrow{\mathrm{AB}}+t\,\overrightarrow{\mathrm{AC}})\cdot\overrightarrow{\mathrm{AB}}=0$$

準備の項で求めている成分をそれぞれ代入して計算すると、

$$0+2s+t=0\tag{1-2}\label{eq1-2}$$

$\overrightarrow{\mathrm{PH}}\perp\overrightarrow{\mathrm{AC}}$

同様に、

$$\overrightarrow{\mathrm{PH}}\cdot\overrightarrow{\mathrm{AC}}=0$$

より\eqref{eq1-1}を代入して、

$$(\overrightarrow{\mathrm{PA}}+s\,\overrightarrow{\mathrm{AB}}+t\,\overrightarrow{\mathrm{AC}})\cdot\overrightarrow{\mathrm{AC}}=0$$

$$\therefore\;3+s+5t=0\tag{1-3}\label{eq1-3}$$

連立方程式を解く

\eqref{eq1-2}\eqref{eq1-3}より、

$$s=\frac13,\quad t=-\frac23$$

$\overrightarrow{\mathrm{PH}}$

$s,\, t$ を\eqref{eq1-1}の $\overrightarrow{\mathrm{PH}} = \overrightarrow{\mathrm{PA}}+s\,\overrightarrow{\mathrm{AB}}+t\,\overrightarrow{\mathrm{AC}}$ に代入し、

$$\overrightarrow{\mathrm{PH}}=\frac23\begin{pmatrix}1\\2\\2\end{pmatrix}$$

答え

$\mathrm{P}(-2,-1,0)$ より、

$$\mathrm{H}\left(-\frac43,\frac13,\frac43\right)$$

2. 垂直：外積

垂線方向とは？

平面 $\alpha$ に垂直ということは $\alpha$ の基底ベクトル $\overrightarrow{\mathrm{AB}}$, $\overrightarrow{\mathrm{AC}}$ に垂直。すなわち、

• $\overrightarrow{\mathrm{PH}}\perp\overrightarrow{\mathrm{AB}}$
• $\overrightarrow{\mathrm{PH}}\perp\overrightarrow{\mathrm{AC}}$

ということです。ここまでは先ほどの 1. と同じです。

ここでは、これら2つを同時に満たす $\overrightarrow{\mathrm{PH}}$ の方向を一発で求めます。それが、外積です。

詳細は下記の記事を参照ください。

垂直：外積

外積を求める

外積は上記の記事を参考にすると次のように求められます。

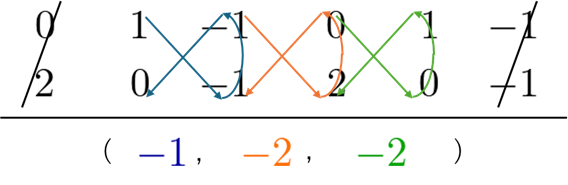
垂直な方向という意味では $-1$ 倍しても同じなので、これは、

$$\overrightarrow{n}=\begin{pmatrix}1\\2\\2\end{pmatrix}$$

としてよいです。

平面 $\alpha$ の方程式

平面 $\alpha$ の方程式は、$\mathrm{A}(0,0,1)$, $\overrightarrow{\mathrm{AB}}=(0,1,-1)$, $\overrightarrow{\mathrm{AC}}=(2,0,-1)$ より、

$$\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}0\\0\\1\end{pmatrix}+s\,\begin{pmatrix}0\\1\\-1\end{pmatrix}+t\,\begin{pmatrix}2\\0\\-1\end{pmatrix}$$

これと $\overrightarrow{n}=(1,2,2)$ と内積を取り、平面 $\alpha$ の方程式は、

$$x+2y+2z=2$$

直線の方程式

平面 $\alpha$ に垂直な方向 $\overrightarrow{n}=(1,2,2)$ が分かったので、点 $\mathrm{P}(-2,-1,0)$ からこの方向に直線を引きます。

$$\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}-2\\-1\\0\end{pmatrix}+u\,\begin{pmatrix}1\\2\\2\end{pmatrix}\tag{2-1}\label{eq2-1}$$

平面との交点

この直線の式を平面 $\alpha:\; x+2y+2z=2$ に代入して $u$ を求めると、

$$u=\frac23$$

答え

これを\eqref{eq2-1}に代入すると $\mathrm{H}$ の座標です。

$$\mathrm{H}\left(-\frac43,\frac13,\frac43\right)$$

関連記事

同じ問題を扱っています。平面の方程式が与えられている場合で、垂線の足までの距離を求めるものです。こちらも見るとより理解が深まります。