余弦定理って、微妙に覚えにくくないですか? 公式の気持ちを理解すれば覚えられます。加えて図形による証明は美しいので一度見ておくとよいでしょう。
余弦定理:$c^2=a^2+b^2-2ab\cos\theta$

気持ち:三平方の定理を微調整
直角三角形と比べる
まず、大雑把な気持ちとして直角三角形を考えます。$\theta=90^\circ$ のケースです。そして、辺 $\mathrm{a}$, $\mathrm{b}$ の長さはそのままに $\theta<90^\circ$ とすると、当然もう一つの辺 $c^\prime$ は元の直角三角形の状態 $c$ よりも短くなります。

hogehoge 部分はいくらか?
問題は短くなる調整項の hogehoge がいくらになるか?です。
三角形の大きさが大きくなればそれに比例して $c$ や $c^\prime$ の長さも大きくなるでしょう。つまり、調整項は $ab$ に比例するはずです。なので、
$$c^{\prime\,2}=a^2+b^2-(\mathrm{hoge})\times ab$$
という形になるはずです。
次に、余弦定理というくらいなので、$\cos\theta$ が出てくるのも想像に難くないと思います。よって、
$$c^{\prime\,2}=a^2+b^2-(\mathrm{hoge})\times ab\cos\theta$$
かな、と想像します。実際、$\theta=90^\circ$ なら $\cos\theta=0$ なので三平方の定理となり、よさそうだと思えます。
そして最後に定数項の $2$ ですが、これは残念ながら覚えておかなくてはならないです。もしくは後に示す証明を少しイメージすれば $2$ は思い出しやすくなります。これで、
$$c^{\prime\,2}=a^2+b^2-2ab\cos\theta$$
を思い出せます。
このように、三平方の定理を基本形としてそれに余弦 $(\cos\theta)$ の調整項がついた形である、と理解するとよいです。
図形による証明:アニメーションで理解
基本形として三平方の定理のアニメーションがあります↓。
証明動画
三平方の定理のアニメーションとほぼ同じですが、隙間ができるところが異なります。この隙間が調整項です。
隙間部分だけ確認
隙間以外の部分は三平方の定理のステップバイステップ解説を確認することにして、ここでは隙間部分だけを確認します。
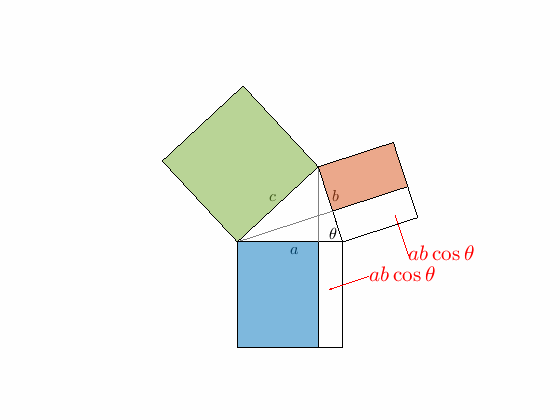
2つの隙間部分の面積はどちらも $ab\cos\theta$
下図で細長いほうの隙間(四角形$\mathrm{LMEB}$)に着目します。

その隙間の辺の長さは、短い方が $\mathrm{LB}=b\cos\theta$ で長い方が $a$ です。従ってその面積は
$$ab\cos\theta$$
になります。もう一つの隙間も同様に $ab\cos\theta$ なので、2つ合わせて
$$2ab\cos\theta$$
となり、これが隙間の面積です。
隙間の面積を引くと、余弦定理の公式
青の四角同士と赤の四角同士は同じ面積なので、
$$c^2=a^2+b^2-2ab\cos\theta$$
が成り立ちます。
式による証明:ベクトルで一発
証明というより、そもそも余弦定理を持ち出さずにベクトルで解いてしまう、という感覚で十分です。下図において求めたいのは $|\overrightarrow{\mathrm{AB}}|^2$ ですので、$\overrightarrow{\mathrm{AB}}$ を $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ で表現します。

\begin{eqnarray}
|\overrightarrow{\mathrm{AB}}|^2 &=& |\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}|^2\\
&=& |\overrightarrow{\mathrm{OB}}|^2-2\,\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}+|\overrightarrow{\mathrm{OA}}|^2\\
&=& |\overrightarrow{\mathrm{OB}}|^2-2\,|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|\cos\theta+|\overrightarrow{\mathrm{OA}}|^2\\
&=& a^2+b^2-2ab\cos\theta
\end{eqnarray}
です。ここでも余弦定理の公式で出てくる定数項の $2$ が表れました。2乗の展開としてです。
まとめ
余弦定理の覚え方についていろいろな角度から眺めてみました。
一つ目は余弦定理の気持ちになることです。具体的には、三平方の定理から始まって角度と辺の長さによる調整項が加わる、という気持ちです。定数項の $2$ についてだけは覚えておく必要があります。
二つ目は美しい図形証明です。これ自体は「へぇー」くらいで眺めてもらえばよいですが、調整項として出てくる空白の長方形が2つできることに注目です。これが調整項に出てくる $2$ です。
最後はベクトルでの計算です。ベクトルは図形の問題を単なる計算問題に落とし込んでくれる便利な道具です。余弦定理を覚えなくてもベクトル化することで解けてしまいます。なおここでも調整項に出てくる $2$ を理解できました。2乗の展開です。


コメント