置換積分は「変数を変えると簡単になる」と説明されますが、その本質は至ってシンプルです。それは、横と縦のスケールを伸縮して、面積を保ったまま関数の形を変える操作です。このイメージをアニメーションとともに丁寧に確認していきます。
置換積分では何が起きているのか
置換積分の本質は、横($x$ 方向)と縦($y$ 方向)のスケールを調整して、面積を保ったまま “扱いやすい形” に変形することです。まずは仕組みがよく見える簡単な例で確認します。
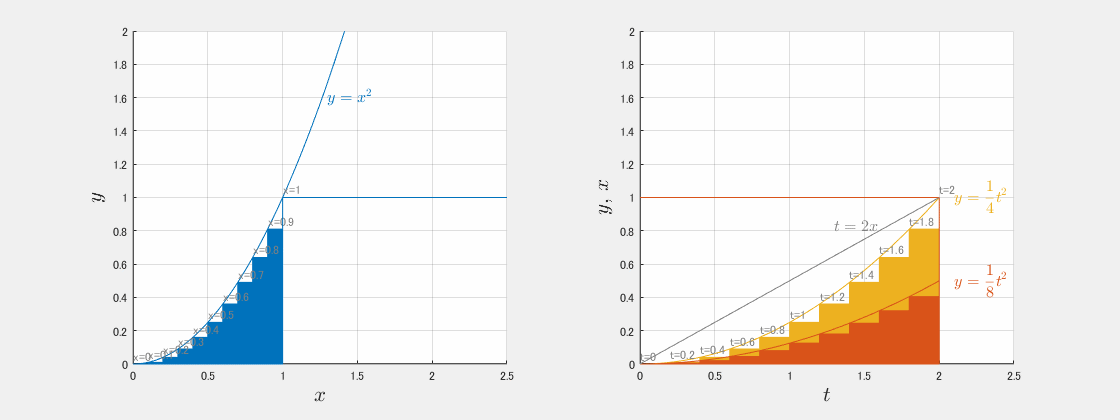
例:$\int_0^1 x^2\, dx$ を $t=2x$ で置換する
計算上のメリットはありませんが、置換積分の仕組みを理解するには最適な例です。
$$\int_0^1 x^2\, dx = \frac{1}{3}$$
これを、
$$t=2x$$
で置換します。すると、
- $y=x^2=\displaystyle\frac14 t^2$(高さは同じ)
- $dt=2dx$(横幅が2倍)
- $x:0\to1$ に対し $t:0\to2$
これらを使うと、
$$\int_0^1 x^2\, dx = \int_0^2 \frac14 t^2 \cdot \frac12 dt=\frac13\tag{1}\label{eq1713-1}$$
となり、当然ながら元の値と一致します。
高さは同じで横幅だけ変わる $y-t$ グラフでは面積はどうなる?
置換 $t=2x$ により $y-t$ グラフ(下図右)は、高さは同じまま、横幅だけ2倍になります。短冊で見ると次のようになります。
横幅が2倍なので 面積も2倍 になってしまいます。つまり、置換しただけでは、
$y$ は同じだが横幅が変わる → 面積がズレる
という状態になります。
横幅が変わった分を縦で補正する
横幅が2倍になったので、面積を保つには縦を1/2に補正すればよいことになります。
これは $dt=2dx$ を変形した
$$dx=\frac12 dt$$
から分かります。この場合、常に1/2倍します。補正のイメージは次の動画です。
これで、赤の面積(置換後$:y-t$ の面積)=青の面積(置換前$:y-x$ の面積)となります。
横と縦のスケール伸縮をひとまとめに見る
$t=2x$ の置換を視覚的に確認します。横軸が $t$、縦軸が $x$ であることに注意してください。縦軸 $x$ が $dx$ だけ増えれば横軸 $t$ は $2dx$ 増えることを直感的に理解するための図です。

この図を用いて先ほどの動画を眺めなおします。
- 横の増え方は、$t=2x$ で制御され、
- 縦の調整は、$dx=\displaystyle\frac12 dt$ の $\displaystyle\frac12$ で制御されます。
横幅が2倍 → 縦を1/2 に補正 → 面積が一致、という流れをまとめて見ると次のようになります。
この例では関数形はほとんど変わりませんが、置換積分の仕組みは完全に見えました。
例題による確認
置換積分の本質は、横と縦のスケールを調整して、面積を保ったまま “簡単な形” に変形することです。ここからは、置換によって「形が劇的に簡単になる」例を見ていきます。
例題1:$\int_0^{\frac{\pi}{2}}\sin x\,\cos x\, dx$
置換すると、なんと $y=t$ の積分になります。
$t=\sin x$ とおくと、$dt=\cos x\,dx$ より、
\begin{eqnarray} \int_0^{\frac{\pi}{2}}\sin x\cos x\,dx &=& \int_0^1 t\,dt = \frac12 \end{eqnarray}
イメージ
- 横の増え方は、$t=\sin x$ で制御され(右の図のグレーのグラフ)、
- 縦の調整は、$dx=\displaystyle\frac{1}{\cos x}\,dt$ の $\displaystyle\frac{1}{\cos x}$ で制御されます。
その結果、左の図の横軸 $x$ (=右の図の縦軸 $x$) が線形に増えていっているのに対し、右の図の横軸 $t$ は $1$ に近づくにつれ歩みが遅くなっています。一方、縦の長さは、左の図の青と右の図の黄が同じ高さですが、$\displaystyle\frac{1}{\cos x}$ で調整した結果右の図の赤になり、それが $y=t$ です。
例題2:$\int_0^1 2x\sqrt{x^2+1}\, dx$
置換すると $y=\sqrt{t}$ の積分になります。
$t=x^2+1$ とおくと、$dt=2x\,dx$ より、
\begin{eqnarray} \int_0^1 2x\sqrt{x^2+1}\,dx &=& \int_1^2 \sqrt{t}\,dt = \frac23(2\sqrt2-1) \end{eqnarray}
イメージ
- 横の増え方は、$t=x^2+1$ で制御され(右の図のグレーのグラフ)、
- 縦の調整は、$dx=\displaystyle\frac{1}{2x}\,dt$ の $\displaystyle\frac{1}{2x}$ で制御されます。
その結果、左の図の横軸 $x$ (=右の図の縦軸 $x$) が $0\rightarrow 1$ に増えていっているのに対し、右の図の横軸 $t$ は $1\rightarrow 2$ になっています。縦の長さは、左の図の青と右の図の黄が同じ高さですが、$\displaystyle\frac{1}{2x}$ で調整した結果右の図の赤になり、それが $y=\sqrt{t}$ です。
例題3:$\int_0^1\frac{1}{x^2+1}\, dx$
置換すると $y=1$ の積分になります。
$x=\tan\theta$ とおくと、$dx=\displaystyle\frac{1}{\cos^2\theta}d\theta$ より、
\begin{eqnarray} \int_0^1\frac{1}{x^2+1}\,dx &=& \int_0^{\frac{\pi}{4}} 1\,d\theta = \frac{\pi}{4} \end{eqnarray}
イメージ
- 横の増え方は、$x=\tan\theta$ で制御され(右の図のグレーのグラフ)、
- 縦の調整は、$dx=\displaystyle\frac{1}{\cos^2 x}\,d\theta$ の $\displaystyle\frac{1}{\cos^2 x}$ で制御されます。
その結果、左の図の横軸 $x$ (=右の図の縦軸 $x$) が $0\rightarrow 1$ に増えていっているのに対し、右の図の横軸 $\theta$ は $0\rightarrow \displaystyle\frac{\pi}{4}$ になっています。一方、縦の長さは、左の図の青と右の図の黄が同じ高さですが、$\displaystyle\frac{1}{\cos^2 x}$ で調整した結果右の図の赤になり、それが $y=1$ です。
まとめ
置換積分の本質は、横と縦のスケールを伸縮して、面積を保ったまま関数形を変形することです。
その仕組みを、まずは $t=2x$ の例で「横幅が変わる → 縦で補正する」という流れとして確認しました。その後、実践的な例題で、置換により関数形が劇的に簡単になる様子を見ました。
このイメージを持って置換積分に取り組むことで、何をしているのかわからないモヤモヤから解放されると幸いです。


コメント