【微分積分学の基本定理】積分は微分の逆演算ですよ！？ その関係、イメージできますか？

　ここでは、積分が微分の逆演算であることを、厳密な証明というよりはイメージで理解します。イメージゆえ、厳密な証明よりもむしろしっくりくると思います。

積分は教科書的には微分の逆演算として導入されます。$F(x)$ を $f(x)$ の原始関数とすると、

$$\int_a^b f(x)\, dx = F(a)-F(b)\tag{1}\label{p922eq1}$$

が成り立つ、と。そして、

$F(x)$ は微分して $f(x)$ になるようなそんな元の関数だ

と。何のことやらと思うと思いますが、この投稿を最後まで読むことで、

そうだよね、それは当然そうなるよね

と思うようになります。

微小変化量の累積が全体の変化量

理解したいゴールの再確認：$\int_a^b f^{\prime}(x)\, dx = f(a)-f(b)$

　ここでは具体的に、$y=f(x)=x^2$ を用いて考えてみます。理解したいゴールは、

$$\int_a^b f^{\prime}(x)\, dx = f(a)-f(b)\tag{2}\label{p922eq2}$$

で、$a=1,\, b=2$ を考えてみます。ここで、式$\eqref{p922eq2}$は式$\eqref{p922eq1}$とちょっと違ってピンと来ないかもしれないので補足します。式$\eqref{p922eq2}$と式$\eqref{p922eq1}$とは次のように対応します。

　式$\eqref{p922eq2}$の関係式が言えれば、式$\eqref{p922eq1}$において「$F(x)$ は微分して $f(x)$ になるようなそんな元の関数だ」と言えるという魂胆です。

　そして、式$\eqref{p922eq2}$の関係を理解するための結論的なイメージは下記のようですが、順番に見ていきます。

$f^{\prime}(x)\, dx$ は図形的に何を表しているか？

　いま一度式$\eqref{p922eq2}$を見ます。左辺の値がどうなるのか、それを示しているのが上の動画なのですが、そのポイントは積分とは何を表しているのか、また $f^{\prime}(x)\, dx$ は図形的には何を表しているかを理解することです。

　まず、積分とは何を表しているか、については【積分のイメージ】積分は細かい短冊の寄せ集めで見たように、細かい短冊の寄せ集めです。式$\eqref{p922eq2}$ の積分に於いその短冊は、
$$f^{\prime}(x)\, dx$$
です。さて、次にこれは図形的には何を表しているか、です。ここで $y=f(x)$ のグラフと絡めてその図形的意味を考えるのがミソです。

それは、元の関数 $f(x)$ の微小区間 $dx$ での変化量！

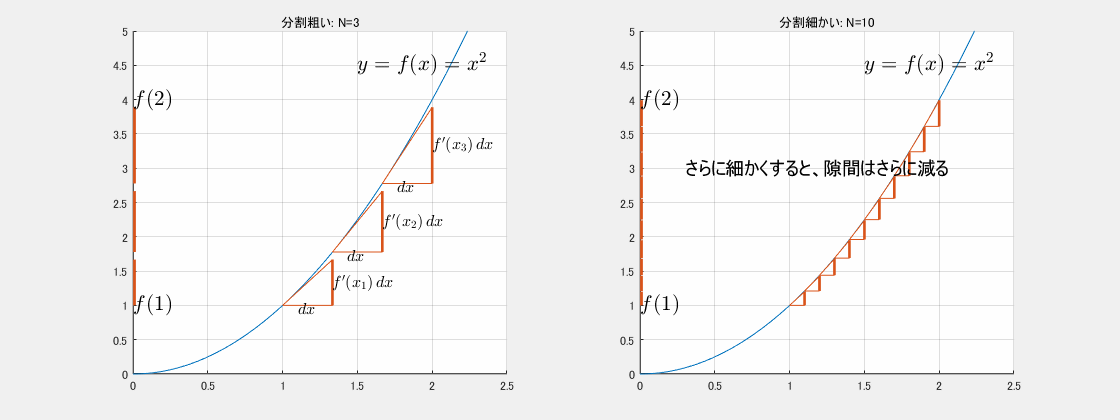
　$f^{\prime}(x)\, dx$ は $y=f(x)$ のグラフに於いては点 $x$ において微小距離 $dx$ だけ進んだ時の $y$ の変化量 $(dy)$ を表しています。次の図は3分割してその様子を確かめたものです。

　具体的には、いま、3分割を考えているので、$x_1=1,$ $x_2=1+\displaystyle\frac{1}{3}=\displaystyle\frac{4}{3},$ $x_3=1+\displaystyle\frac{2}{3}=\displaystyle\frac{5}{3}$ であり、$dx=\displaystyle\frac{1}{3}$ です。また、$f(x)=x^2$ の微分 $f^{\prime}(x)$ は $2x$ なので、

• $f^{\prime}(x_1)\, dx = 2x_1\, dx =2\cdot 1\cdot\displaystyle\frac{1}{3}=\frac{6}{9}$
• $f^{\prime}(x_2)\, dx = 2x_2\, dx =2\cdot\displaystyle\frac{4}{3}\cdot\displaystyle\frac{1}{3}=\frac{8}{9}$
• $f^{\prime}(x_3)\, dx = 2x_3\, dx =2\cdot\displaystyle\frac{5}{3}\cdot\displaystyle\frac{1}{3}=\frac{10}{9}$

より、

$$\begin{eqnarray} 微小長さの合計 &=& f^{\prime}(x_1)\, dx + f^{\prime}(x_2)\, dx + f^{\prime}(x_3)\, dx\\ &=& \frac{6}{9}+\frac{8}{9}+\frac{10}{9}\\ &=&\frac{24}{9}\\ &=&2.66\cdots \end{eqnarray}$$

となります。これは、$f(2)-f(1)=2^2-1^2=3$ に近いですが、隙間があります。

　実際、$f^{\prime}(x_i)\, dx$ を $y$ 軸に寄せていったとき、$f(1)$ から $f(2)$ の間に若干の隙間があることが分かります。しかしここではその隙間はあまり重要ではありません。なぜなら、$dx$ とは本来は3分割という粗い分割ではないからです。次の図は10分割です。

　次の図は100分割です。

それを足し合わせたものが $\int_a^b f^{\prime}(x)\, dx$

　もっと細かい $dx$ で分割したときの $f^{\prime}(x_i)\, dx$ の寄せ集めが、
$$\int_1^2 f^{\prime}(x)\, dx$$
です。そしてその寄せ集められた結果は、
$$f(2)-f(1)$$
になることはこれまでの図からわかるでしょう。これが、積分は微分の逆演算であるイメージです。

まとめ

　微分が積分の逆演算であることを理解しました。

$$f^\prime(x)\, dx$$

というのが $y=f(x)$ の微小区間 $dx$ での $y$ の変化量 $dy$ を表しており、その総和である

$$\int_a^b f^\prime(x)\, dx$$

が $y=f(x)$ の $x=a$ から $x=b$ までの $y$ の変化量 $(f(b)-f(a))$ を表します。すなわち、

$$\int_a^b f^\prime(x)\, dx = f(b) – f(a)$$

となるわけです。