「空間での直線の表し方」では、 「基準点+t×方向ベクトル」 という直線の型を学びました。
この記事では、その型の理解を深めるために、 まず 2次元で $t$ を消去して軌跡方程式を作る感覚 をつかみます。それには法線ベクトルを使うと $t$ が一瞬で消えます。3次元よりもイメージしやすいので、 軌跡方程式の本質がよりクリアになります。
空間での直線の表し方:
1. 例題:$\mathrm{A}(1,2)$, $\mathrm{B}(2,3)$ を通る直線の式
まずは、2点 $\mathrm{A}(1,2)$, $\mathrm{B}(2,3)$ を通る直線を考えます。
1-1. 方向ベクトルを求める
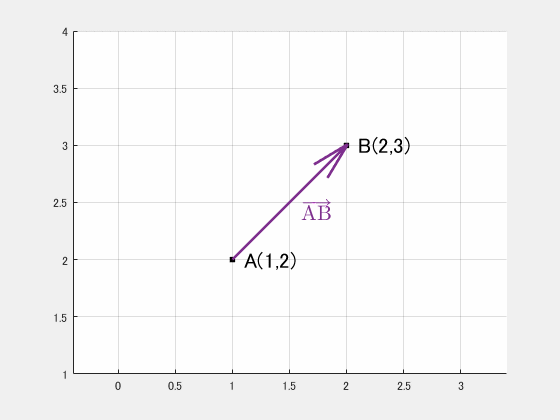
$$\overrightarrow{\mathrm{AB}}=\begin{pmatrix}2\\3\end{pmatrix}-\begin{pmatrix}1\\2\end{pmatrix}=\begin{pmatrix}1\\1\end{pmatrix}$$
(図)$\mathrm{A} → \mathrm{B}$ の方向ベクトル
1-2. ベクトル方程式を立てる
基準点を $\mathrm{A}$ とすると、
$$\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}1\\2\end{pmatrix}+t\begin{pmatrix}1\\1\end{pmatrix}\tag{1}\label{p8526eq1}$$
(図)ベクトル方程式のイメージ
2. 成分表示に書き下す
ベクトル方程式を成分ごとに書くと、
\begin{eqnarray}
\left\{\begin{array}{l}
x &=& 1 + t\\
y &=& 2 + t
\end{array}\right.
\end{eqnarray}
となります。
3. $t$ を消去して軌跡方程式を求める
それぞれを $t =$ の形にすると、
\begin{eqnarray}
\left\{\begin{array}{l}
t &=& x – 1\\
t &=& y – 2
\end{array}\right.
\end{eqnarray}
よって、
$$x – 1 = y – 2$$
これが 軌跡方程式 です。
参考記事:$t$(パラメータ)を消去して軌跡方程式になることは下記で詳しく扱っています。
4. 見慣れた形に直すと…
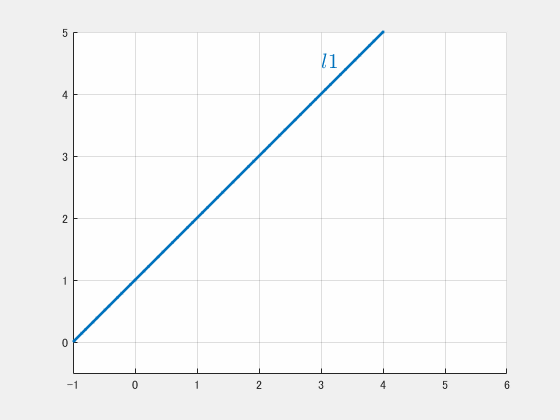
$$y = x + 1$$
これは中学のときから見慣れている直線の式ですね。
(図)最終的な直線のグラフ
5. 法線ベクトルとの内積を取って $t$ を消去する方法
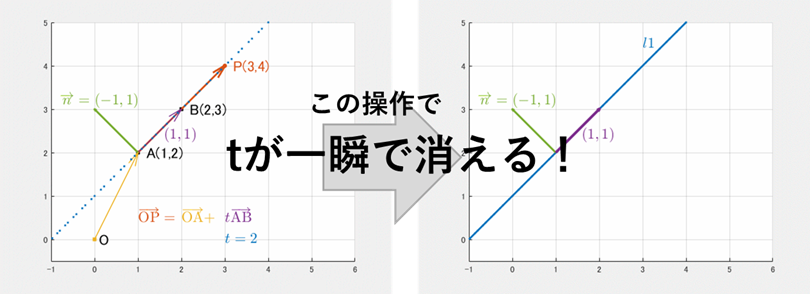
ここまでは、成分表示にして $t$ を代入して消す方法 を見てきました。 実は、直線の方向と垂直なベクトル(法線ベクトル)を使うと、 一瞬で $t$ が消えます。
式\eqref{p8526eq1}
$$\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}1\\2\end{pmatrix}+t\begin{pmatrix}1\\1\end{pmatrix}\tag{1:再掲}$$
の両辺をベクトル
$$\begin{pmatrix}1\\-1\end{pmatrix}$$
で内積を取ります。すると $t$ が消え、瞬時に
$$x-y=-1$$
を得ます。
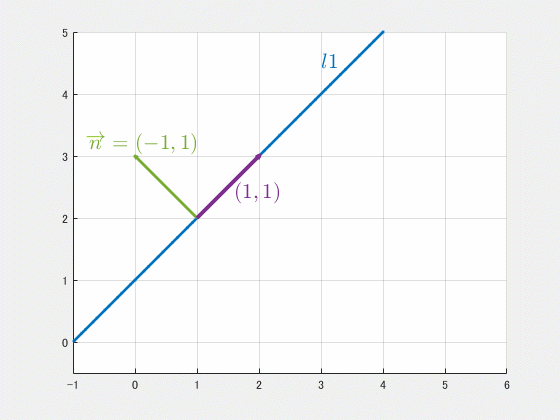
5-1. パラメータを消去するための法線ベクトル
$t$ が消えたのは、
内積を取った $\begin{pmatrix}1\\-1\end{pmatrix}$ が
直線の方向である $\begin{pmatrix}1\\1\end{pmatrix}$ と垂直
だからです。
この $\begin{pmatrix}1\\-1\end{pmatrix}$ のことを
法線ベクトル
といいます。法線ベクトルで内積を取ることで、パラメータを消去することができます。
これは、3次元でも同じように適用でき、その場合は平面の軌跡方程式が得られます。
5-2. 法線ベクトルの意味
直線 $ax+by+c=0$ の法線ベクトルは
$$\begin{pmatrix}a\\b\end{pmatrix}$$
ですが、この意味がよく分かります。
つまり、直線の式に含まれる $a$, $b$ は、 直線の向きと垂直な方向を表しています。
6. まとめ
- ベクトル方程式は「動く点」を表す式
- 成分表示にすると $t$ が見える
- $t$ を消去すると軌跡方程式になる
- 2次元では見慣れた $ax+by+c=0$ の形に戻る
- 法線ベクトルで内積を取れば瞬時に $t$ が消去できる
- 3次元でも同じ流れで軌跡方程式を作れる(平面の式)
次の記事では、 今回学んだ「基準点+t×方向ベクトル」の考え方を使って、 内分点・外分点をベクトル方程式で統一的に扱う方法 を見ていきます。
内分点・外分点の公式を覚えなくても、 ベクトル方程式だけでそれらが求められることが実感できます。





コメント