この公式を使うとすごく時短になります。しかし覚えずにいつでもすぐに導いて使うのが得策です。単に覚えると間違いの元です。
そして使用面でのこの公式のうま味は、二次方程式の解を実際に求めなくても解と係数の関係から簡単に積分が実行できるところです。
1/6公式だけではなく、1/3公式や1/12公式も同じように使えるので、合わせてみてください。
放物線と直線で囲まれた面積：公式
$$\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)\, dx=-\frac{1}{6}(\beta-\alpha)^3$$
証明は後ほど示します。ここでは、
- 面積なのになぜマイナスがついている？
とか、
- これが放物線と直線で囲まれた面積を表すのがちょっとピンとこない
とかいったところを解消します。
面積なのになぜマイナスがついている？
最初に結論を言ってしまえば、この式の場合、
- 求めている面積は負の領域にあるから
です。
$x$ が $\alpha$ と $\beta$ の間にあるとき、被積分関数の $(x-\alpha)(x-\beta)$ の値は負です。負の値を足していっているのでその合計値は負になります。
これが放物線と直線で囲まれた面積を表すのがちょっとピンとこない
こう思う人は、先ほどの被積分関数のどこに直線の要素があるのか、というのがピンと来ていないものと思います。先ほどの被積分関数の場合は $y=0$ とで囲まれた面積を求めているということになります。ただし、値が負になっていることからもわかる通り、正確には「囲まれた面積」ではないです。「囲まれた面積」を求めるには、上側の関数から下側の関数を引くことにより長さを正としておく必要があるので、この場合は、$y=0$ から $y=(x-\alpha)(x-\beta)$ を引いて、
$$S=\int_{\alpha}^{\beta}\left\{0-(x-\alpha)(x-\beta)\right\} \, dx = \frac{1}{6}(\beta-\alpha)^3$$
となります。
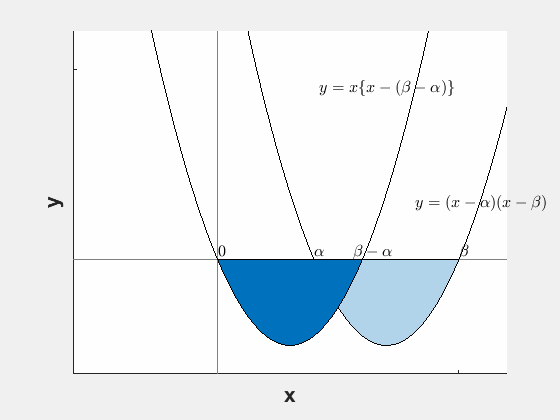
証明：平行移動すると楽
平行移動
もちろん、強引に展開して計算すればできます。しかし冒頭でも述べたように
いつでもすぐに導いて使う
ためには少し工夫したいです。工夫は、
平行移動
です。次のように↓平行移動します。
つまり、
\begin{eqnarray}
S &=& \int_{\alpha}^{\beta}(x-\alpha)(x-\beta)\,dx\\
&=& \int_0^{\beta-\alpha}x\{x-(\beta-\alpha)\}\,dx
\end{eqnarray}
と変形して計算するわけです。
証明
\begin{eqnarray}
S &=& \int_{\alpha}^{\beta}(x-\alpha)(x-\beta)\,dx\\
&=& \int_0^{\beta-\alpha}x\{x-(\beta-\alpha)\}\,dx\\
&=& \int_0^{\beta-\alpha}\{x^2-x(\beta-\alpha)\}\,dx\\
&=& \left[\frac{1}{3}x^3-\frac{1}{2}x^2(\beta-\alpha)\right]_0^{\beta-\alpha}\\
&=& -\frac{1}{6}(\beta-\alpha)^3
\end{eqnarray}
毎回この式変形をしていれば、そしてグラフを同時に思い浮かべれば、
- マイナスがついていること
- その係数が $\displaystyle\frac{1}{6}$ であること
- 元の二次関数の二次の係数が $a$ なら単に $a$ 倍すればよいこと
- $3$ 乗であること（$x^2$ の積分なので）
などが否が応でも理解できます。そしてこれを繰り返しているうちに本当に覚えられます。
例題1. 解と係数の関係が活躍する公式の基本形
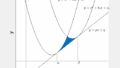
放物線 $y=x(x-3)$ と直線 $y=x-2$ とで囲まれた部分の面積 $S$ を求めよ。
求める面積は図の青で塗られている部分であり、直線の式から放物線の式を引けばよいです。
公式を用いて計算
解
$y=x(x-3)$ と $y=x-2$ の交点の $x$ 座標は $x(x-3)=x-2$ より、
$$x^2-4x+2=0$$
これの2つの解を $\alpha,\,\beta\,(\alpha <\beta)$ とすると、解と係数の関係より
$$\alpha +\beta=4,\;\; \alpha\beta=2$$
よって求める面積 $S$ は、
\begin{eqnarray}
S&=&\int_{\alpha}^{\beta}\{-(x^2-4x+2)\}\, dx = \frac{1}{6}(\beta -\alpha)^3\\
&=&\frac{1}{6}\left\{\sqrt{(\alpha +\beta)^2-4\alpha\beta}\right\}^3\\
&=&\frac{1}{6}\left\{\sqrt{4^2-4\times 2}\right\} ^3\\
&=&\frac{1}{6}\left\{\sqrt{8}\right\} ^3\\
&=&\frac{8\sqrt{2}}{3}
\end{eqnarray}
まじめに計算
解
$y=x(x-3)$ と $y=x-2$ の交点の $x$ 座標は $x(x-3)=x-2$ より、
$$x^2-4x+2=0$$
これを解くと、
$$x=2\pm\sqrt{2}$$
よって求める面積 $S$ は、
\begin{eqnarray}
S&=&\int_{2-\sqrt{2}}^{2+\sqrt{2}}\{-(x^2-4x+2)\}\, dx = -\left[\frac{1}{3}x^3-2x^2+2x\right]_{2-\sqrt{2}}^{2+\sqrt{2}}\\
&=&-\bigg[\left\{\frac{1}{3}(2+\sqrt{2})^3-2(2+\sqrt{2})^2+2(2+\sqrt{2})\right\}\\
&&\;\,-\left\{\frac{1}{3}(2-\sqrt{2})^3-2(2-\sqrt{2})^2+2(2-\sqrt{2})\right\}\bigg]\\
\end{eqnarray}
この計算をするのは骨が折れますので、Wolfram Alphaに解いてもらいましょう。すると、
$$=\frac{8\sqrt{2}}{3}$$
となることが分かります。
例題2. 公式を使うと最大最小問題の見通しがよいという例
放物線 $y=x(x-3)$ と直線 $y=m(x-2)$ とで囲まれた部分の面積 $S$ が最小となるように、定数 $m$ の値を求めよ。また、その時の面積 $S$ の値を求めよ。
先ほどはこの問題の $m=1$ のケースを考えたことになっています。先ほどの問題を解いた狙いは、この問題を見た際に $m$ の値を決めれば面積 $S$ は決まる、というイメージをつかんでもらうことです。$m$ の値を決めれば直線が決まり、そうすると面積が決まる、というイメージをつかむことです。次の図のようです。
このイメージが持てれば、解答は先ほどの $m=1$ の場合とほぼ同じです。
公式を用いて計算
解
$y=x(x-3)$ と $y=m(x-2)$ の交点の $x$ 座標は $x(x-3)=m(x-2)$ より、
$$x^2-(m+3)x+2m=0$$
これの2つの解を $\alpha,\,\beta\,(\alpha <\beta)$ とすると、解と係数の関係より
$$\alpha +\beta=m+3,\;\; \alpha\beta=2m$$
よって求める面積 $S$ は、
\begin{eqnarray}
S&=&\int_{\alpha}^{\beta}\left\{-\left( x^2-(m+3)x+2m\right)\right\}\, dx = \frac{1}{6}(\beta -\alpha)^3\\
&=&\frac{1}{6}\left\{\sqrt{(\alpha +\beta)^2-4\alpha\beta}\right\}^3\\
&=&\frac{1}{6}\left\{\sqrt{(m+3)^2-4\times 2m}\right\} ^3\\
&=&\frac{1}{6}\left\{\sqrt{m^2-2m+9}\right\} ^3\\
&=&\frac{1}{6}\left\{\sqrt{(m-1)^2+8}\right\} ^3\\
&\geqq&\frac{1}{6}\left\{\sqrt{8}\right\} ^3\\
&=&\frac{8\sqrt{2}}{3}
\end{eqnarray}
等号は、$m=1$ のとき。
まとめ
放物線の1/6公式を理解し、例題を見てきました。1/6公式のうま味は、二次方程式の解を実際に求めなくても解と係数の関係から簡単に積分が実行できるところです。しかし一方でこれは単に計算のテクニックに過ぎず、真面目に計算を実行すれば解は得られるということも忘れてはなりません。公式を覚えることを目的にしないようには注意しましょう。
1/6公式だけではなく、1/3公式や1/12公式も同じように使えるので、合わせてみてください。
コメント