力学的エネルギー保存の法則は運動方程式に $v$ を掛けて時間で積分すると得られます。もしくは、仕事の定義に運動方程式を代入すると得られます。加えて、各種の位置エネルギーも導出します。
重力の位置エネルギー: $mgh$
弾性エネルギー: $\displaystyle\frac{1}{2}kx^2$
万有引力の位置エネルギー: $-G\displaystyle\frac{Mm}{r}$
電位: $k\displaystyle\frac{Qq}{r}$
その際、重力の位置エネルギーと等加速度運動の公式の一つである $v^2-v_0^2=2as$ が実は同じものであることも見えてきます。
力学的エネルギー保存の法則
運動方程式に $v$ を掛けて積分する
運動方程式
$$m\frac{dv}{dt}=F$$
の両辺に速度 $v\left(=\displaystyle\frac{dx}{dt}\right)$ を掛けて $t$ で積分すると、
$$\int_{t=t1}^{t=t2}mv\frac{dv}{dt}\, dt = \int_{t=t1}^{t=t2}F\frac{dx}{dt}dt$$
見やすさのため、左辺と右辺を別々に計算を進めます。
\begin{eqnarray}
左辺&=&\int_{v=v_1}^{v=v_2}mv\, dv=\frac{1}{2}m\left[v^2\right]_{v_1}^{v_2}=\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2\\
右辺&=&\int_{x=x_1}^{x=x_2}F\, dx=W
\end{eqnarray}
ここで、変数変換に於いてはそれぞれの添え字に対応する変数名に変換しています。また、$W$ は外力 $F$ がなした仕事です。よって、次の力学的エネルギー保存の法則が導かれます。
$$\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2=W$$
これは、なされた仕事の量だけ運動エネルギーが増加するということでありまた逆に、運動エネルギーを持った物体は仕事をすることができる、ということでもあります。
仕事の定義に運動方程式を代入する
同じことですが、仕事の定義 $W=\displaystyle\int F\, dx$ に運動方程式 $F=m\displaystyle\frac{dv}{dt}$ を代入しても得られます。
\begin{eqnarray}
W &=& \int_{x=x_1}^{x=x_2} F\, dx = \int_{x=x_1}^{x=x_2} m\frac{dv}{dt}\, dx = \int_{v=v_1}^{v=v_2} m\frac{dx}{dt}\, dv\\
&=& \int_{v=v_1}^{v=v_2}mv\, dv=\frac{1}{2}m\left[v^2\right]_{v_1}^{v_2}=\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2
\end{eqnarray}
これをパッと見で見やすく一行で表すと下記のようです。見やすさのため、積分区間の下端と上端は省略します。

類似記事として↓も参考に見てみてください。こちらの記事では、$\displaystyle\frac{1}{2}$ が出てくるところにスポットを当てた説明をしています。
様々な力による位置エネルギー
重力の位置エネルギー
重力が行った仕事で定義する
重力は $F=-mg$ なので、高さ $h$ から $0$ まで落下することを考えると、重力が行った仕事は

\begin{eqnarray}
W&=&\int_{h}^{0}(-mg)\, dx\\
&=& -mg[h]_{h}^{0}\\
&=&mgh
\end{eqnarray}
となるから、
$$\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2=mgh\tag{1}\label{p1244eq1}$$
このとき、もともとあった $mgh$ は位置が持っていた潜在的なエネルギーととらえ、位置エネルギーと言います。また、潜在的な、は英語でポテンシャルというため、ポテンシャルエネルギーとも言います。
重力の位置エネルギー: $mgh$
実は等加速度運動の公式と同じ
さて、ここで式\eqref{p1244eq1}を見てピンときた人は鋭いです。【等加速度運動の3公式】微分積分を用いて導出し、完全理解の3つ目の公式に近い形をしていますね。実際、両辺に $2$ を掛けてさらに $m$ で割り、さらに重力加速度を $a$ と、高さ $h$ を $s$ と書くと式\eqref{p1244eq1}は
$$v_2^2-v_1^2=2as$$
となり、等加速度運動で出てきた公式が得られました。つまり、加速度 $a$ で等加速度運動をしている物体の問題を扱うときには、それは重力加速度が $a$ の世界で力学的エネルギー保存の法則を用いて問題を解いているのと同じことをしている、ということを表しています。
仕事がため込まれるという考え方で定式化する
先ほどは重力が行った仕事でポテンシャルエネルギーを定義しました。もちろんこれで全く問題ないのですが、同じことを裏の角度からとらえることもできます。それは、質量 $m$ の物体を位置 $0$ から位置 $h$ まで重力に逆らって、例えばあなたが持ち上げた、と考えます。そして、あなたが行った仕事が位置のエネルギーとして蓄えられた、と考えるのです。図で表すと下図のようです。

\begin{eqnarray}
W&=&\displaystyle\int_0^h mg\,dx\\
&=&mg\left[x\right]_0^h\\
&=&mgh
\end{eqnarray}
この考え方では先ほどよりも符号がしっくりとする感じがして、私はこちらの考え方の方が好きなのですが、皆さんはどうでしょうか。以降、こちらの考え方で進めます。
弾性エネルギー
ばねは位置 $x$ で物体に $F_{ばね}=-kx$ の力を働かせます。あなたは位置 $0$ から位置 $x$ までこの力に逆らって、つまり $F_{あなたの手}=kx$ でばねを引っ張ります。その時にあなたの手がばねに対して行った仕事がばねに蓄えられ、それは

\begin{eqnarray}
W&=&\int_{0}^{x}kx\, dx\\
&=& k\frac{1}{2}\left[x^2\right]_{0}^{x}\\
&=&\frac{1}{2}kx^2
\end{eqnarray}
となるから、
$W_{弾性エネルギー}= \displaystyle\frac{1}{2}kx^2$
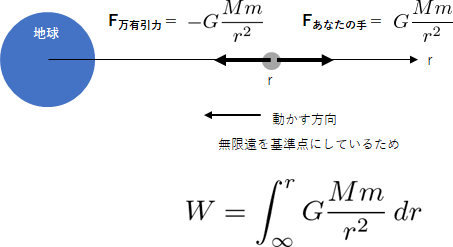
万有引力の位置エネルギー
万有引力は位置 $r$ で物体に $F=-G\frac{Mm}{r^2}$ の力を働かせます。ここで、万有引力の位置エネルギー基準点は無限遠 ($r=\infty$) に取ります。従ってあなたは位置 $\infty$ から位置 $r$ までこの力に逆らって、つまり $F_{あなたの手}=G\frac{Mm}{r^2}$ で物体を引っ張ります。引っ張るといっても、引っ張っている方向と逆の方向に進んでいるのであなたは負の仕事をしていることに注意してください。さて、あなたの手が万有引力に対して行った仕事が万有引力に蓄えられ、それは

\begin{eqnarray}
W&=&\int_{\infty}^{r}G\frac{Mm}{r^2}\, dr\\
&=& -GMm\left[\frac{1}{r}\right]_{\infty}^{r}\\
&=&-G\frac{Mm}{r}
\end{eqnarray}
となるから、
$W_{万有引力の位置エネルギー}=-\displaystyle G\frac{Mm}{r}$
改めて、この値は負になっていることに注意してください。無限遠を基準にしていてそこから落ちてきているところの位置エネルギーなので負です。
外力が電荷の場合: 電位
電荷 $+Q$ は位置 $r$ で電荷 $+q$ に $F=-k\frac{Qq}{r^2}$ の力を働かせます。ここで、電荷の位置エネルギーの基準点は無限遠 ($r=\infty$) に取ります。従ってあなたは位置 $\infty$ から位置 $r$ までこの力に逆らって、つまり $F_{あなたの手}=-k\frac{Qq}{r^2}$ で物体を引っ張ります。その時にあなたの手が電荷 $+q$ に対して行った仕事が電荷 $+q$ に蓄えられ、それは

\begin{eqnarray}
W&=&\int_{\infty}^{r}\left(-k\frac{Qq}{r^2}\right)\, dr\\
&=& kQq\left[\frac{1}{r}\right]_{\infty}^{r}\\
&=&k\frac{Qq}{r}
\end{eqnarray}
となります。
ただし、電位の場合はさらに少し注意が必要です。電位は+1[C]当たりの位置エネルギーと定義されるためです。この場合は $+q$ が+1[C]ということです。そして特にこの値は $V$ と表現されます。従って、
$V=\displaystyle k\frac{Q}{r}$
まとめ
力学的エネルギー保存の法則を、運動方程式を積分することで求めました。運動方程式は各瞬間瞬間で成り立つ式であり、それを積分するということは最初と終わりだけで物事を捉えるということです。
そして、運動方程式の「力」の部分を具体的なものを設定することにより、各種の保存則が導かれました。力が重力なら位置エネルギー $mgh$、ばねなら弾性エネルギー $\displaystyle\frac{1}{2}kx^2$ という具合です。
力学的エネルギー保存の法則も運動方程式と本質的には同じであり、どちらを使うのかはいかに楽に解くのかというテクニックの問題であることが理解でき、気が楽になります。
コメント