【等加速度運動の3公式】微分積分を用いて導出し、完全理解

　等加速度運動の公式は次の式です。

この投稿では等加速度運動の公式を微分積分を用いて完全に理解することを目的にします。これらにより公式をむりに覚えようとせずとも覚えられるだけでなく、3つ目の公式は実は力学的エネルギー保存の法則とつながりがあることも理解できます。

そのため、まずは①グラフを書いて公式を導くことでその本質をイメージし、次に②微分積分を用いはするが多分にグラフに頼ることでその扱いに慣れ、最後に③微分積分の式変形だけで公式を導きます。この①②③が頭の中でつながることがゴールです。

なお、この公式の代表的な応用例は、放物運動の問題です。無味乾燥な問題ではつまらないので、趣味のテニスに適用して考えてみました↓ので、興味ある方はご覧ください。

グラフを書いて公式を導出

　ここではグラフをより具体的に書くため、題材として新幹線を考えてみます。新幹線の加速度はおよそ $2.0\mathrm{[km/h/s]}$ だそうです(参考文献：700系の加速度向上について)。$2.0\mathrm{[km/h]}$ はおよそ $0.5\mathrm{[m/s]} (\simeq 2.0\div 3.6)$ なので、ここでは簡単のため新幹線は $0.5\mathrm{[m/s^2]}$ の一定加速度で加速しているとして考えてみましょう。

加速度 $a$ から速度 $v$ を導出

　ここでは等加速度運動を扱っています。つまり加速度 $a\mathrm{[m/s^2]}$ が時刻 $t\mathrm{[s]}$ に対して一定です。従って、加速度のグラフを書くと下図のようです。

　では、速度はどうなるでしょうか。新幹線に乗っていることをイメージしてください。新幹線は加速しています。それも、毎秒 $0.5\mathrm{[m/s]}$ ずつ速度を増して。これがイメージできれば $t\mathrm{[s]}$ 後の速度は $0.5t\mathrm{[m/s]}$ になることもまたイメージ容易でしょう。グラフで表すと下図のようです。

　つまり、「加速度とは単位時間当たりの速度の増加量である」という定義に基づけば、加速度 $a$ とは上図である速度-時間グラフ( $v-t$ グラフ)の傾きです。そして、等加速度運動とは加速度 $a$ が一定の運動であるので、そのグラフは直線になります。

　みなさんは今、新幹線はちょうど駅を出発したところからイメージしたと思います。つまり、$t=0$ での速度（初速度という） $v_0$ は $0$ でした。しかし、どの初速度からこれを考え始めても状況は全く同じなので初速度を $v_0$ と置けば、冒頭の公式、
$$v=v_0+at$$
となります。

　さて、最後に少しおまけですが、新幹線は何秒で最高速度 $270\mathrm{[km/h]}$ に到達するでしょうか。ここでは簡単のため、あくまでも一定の加速度 $0.5\mathrm{[m/s^2]}$ で加速しているとして考えます。$270\mathrm{[km/h]}$ は $75\mathrm{[m/s]}$ なので($=270\div 3.6$)、$150\mathrm{[s]}$ で最高速度に到達します。グラフで表すと下記です。

　もちろん実際には最高速度に近づくにつれて加速度は小さくなってくるので、それを考慮すれば $150$ 秒 よりは長くなるでしょう。実際、700系の加速度向上についてにはその2ページ目をみると、$300$ 秒弱で到達することが書かれています。

速度 $v$ から変位 $s$ を導出

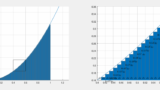
　それでは先ほどの続きで、新幹線が最高速度に到達するときには駅からどこまで離れているでしょうか？動いた距離（変位）は、速度が一定なら 速度$\times$時間 で表されます。このとき $v-t$ グラフを書いたなら、変位 $s$ はその $v-t$ グラフで囲まれる面積であることは明らかです(下図)。

　速度が一定でなくてもこの考えは同じです。すなわち、変位 $s$ は $v-t$ グラフで囲まれる面積です。これは、上のように長方形でそのことが言えれば任意の曲線においてもその面積は微小な長方形の集まりと見なせるので同じことが言えます。

　速度が一定でなくてもこの考えは同じです。すなわち、変位 $s$ は $v-t$ グラフで囲まれる面積です。これは、上のように長方形でそのことが言えれば、【積分のイメージ】積分は細かい短冊の寄せ集めで見たように任意の曲線においてもその面積は微小な長方形の集まりと見なせるので同じことが言えます。

　従って、加速度 $a$ で等加速している場合は下図のようになります。

　変位 $s$ は $v-t$ グラフでの面積なので、図では台形の面積を求めればよく、従って、
$$s=v_0 t+\displaystyle\frac{1}{2}at^2$$
となります。

　新幹線の例に戻りましょう。新幹線は $0.5\mathrm{[m/s^2]}$ で加速しており、$0$ 秒から $150$ 秒までの変位は下図の面積で求められます。

時刻 $t$ を消去した式を導出

　ここまでできればあとは次の問題を解くことに帰着します。

解

上の式は $at=v-v_0$ と変形できる。一方下の式の両辺を $2a$ 倍すると
$$2as = 2v_0\cdot at + (at)^2$$
となるので、ここに $at=v-v_0$ を代入すると、

$$\begin{eqnarray} 2as&=&2v_0(v-v_0)+(v-v_0)^2\\ &=&(v-v_0)\{2v_0+(v-v_0)\}\\ &=&(v-v_0)(v+v_0)\\ &=&v^2-v_0^2 \end{eqnarray}$$

となる。

実は力学的エネルギー保存の法則と同じ式

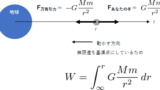
　ところで、この式の形をみてピンときた人はものすごく鋭いです。両辺を $2$ で割ってかつ $m$ をかけ、次の形に変形したらどうでしょう。ついでに加速度 $a$ を重力加速度 $g$ と、移動距離 $s$ を $h$ と書いてみます。すると、
$$\frac{1}{2}mv^2-\frac{1}{2}mv_0^2=mgh$$
となり、力学的エネルギー保存の法則が出てきました。つまり、加速度 $a$ で等加速度運動している物体の問題を扱うときには、それは重力加速度が $a$ の世界で力学的エネルギー保存の法則を用いて問題を解いているのと同じことをしている、ということを表しています。力学的エネルギー保存の法則については、【力学的エネルギー保存の法則】運動方程式を積分して導出し、完全理解に詳しく述べています。

微分積分を用いて公式を導出するが多分にグラフに頼る

　ここでは上記で見てきた導出を、少しだけ微分積分を用いて行います。それは、より抽象的で一般化した次の章を理解するための緩衝材的な役割をします。

加速度 $a$ から速度 $v$ を導出

　加速度 $a$ とは単位時間当たりの速度の変化量です。微小な時間 $dt$ の間に速度が $dv$ だけ変化したとすると単位時間当たりの変化量は $dv\div dt$ です。すなわち、
$$a=\displaystyle\frac{dv}{dt}$$
です。つまり、加速度 $a$ は $v-t$ グラフの傾きです。従って等加速度運動を考えた場合は $v-t$ グラフは傾き一定、つまり直線となりますから、初速度を $v_0$ とすると、任意の時刻 $t$ における速度 $v$ は、
$$v=v_0+at$$
となります。

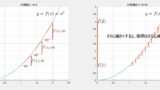
　同じことをもう少し微分積分感を出して別の側面から説明すると、$a=\displaystyle\frac{dv}{dt}$ は $dv=a\, dt$ なので、速度の変化量 $dv$ は $a-t$ グラフの面積で表されます。先ほどと微妙に主語が異なっていることに注意してください。両者の違いをイメージで表現すると下図のようです。

いま、$a$ は一定なので、$a-t$ グラフは下図のようです。

従って
$$v-v_0=at$$
となり、同じ式が導かれます。この操作は積分であることに気づいたでしょうか？式$\eqref{p1125eq1-2}$を中心に、式$\eqref{p1125eq1-1}$から$\eqref{p1125eq1-3}$への式変形と上記の説明とを見比べてください。

速度 $v$ から変位 $s$ を導出

　速度 $v$ とは単位時間当たりの位置の変化量（変位）です。微小な時間 $dt$ の間に位置が $ds$ だけ変化したとすると単位時間当たりの位置の変化量（変位）は $ds\div dt$ です。すなわち、
$$v=\displaystyle\frac{ds}{dt}$$
です。つまり、速度 $v$ は $s-t$ グラフの傾きです。また一方この式は $ds=v\, dt$ なので、位置の変化量（変位） $ds$ は $v-t$ グラフの面積で表されます。

　$a$ が一定のとき $v$ は一次関数 $v=v_0+at$ なので、$v-t$ グラフは下図のようです。

　なお、$s$ は変位（位置の変化量）なので $s=x-x_0$ です。よってこの式は、
$$x=x_0+v_0t+\displaystyle\frac{1}{2}at^2$$
とも書けます。ここも先ほどと同様、$\eqref{p1125eq2-2}$を中心に、式$\eqref{p1125eq2-1}$から$\eqref{p1125eq2-3}$への式変形と上記の説明とを見比べてください。

微分積分の式変形だけで公式を導出

　ここではより一般に応用が利くよう、部分積分を用いた式変形で導きます。

加速度 $a$ から速度 $v$ を導出

加速度は
$$a=\frac{dv}{dt}\tag{1-1}\label{p1125eq1-1}$$
より、両辺を $t$ で $t=0$ から $t=t$ まで積分すると、
$$\int_0^t a\, dt=\int_0^t\frac{dv}{dt}dt\tag{1-2}\label{p1125eq1-2}$$

$a$ は $t$ によらず一定なので積分の外に出せるから、

$$\begin{eqnarray} \mathrm{左辺}&=&a\displaystyle\int_0^t\, dt\\ &=&a[t]_0^t\\ &=&at \end{eqnarray}$$

一方右辺は、$t=0$ のときの速度を $v=v_0$、$t=t$ のときの速度を $v=v_t$ と置くと、

$$\begin{eqnarray} \mathrm{右辺}&=&\displaystyle\int_{t=0}^{t=t}\displaystyle\frac{dv}{dt}dt\\ &=& \displaystyle\int_{v=v_0}^{v=v_t}\, dv\\ &=& [v]_{v_0}^{v_t}\\ &=& v_t-v_0 \end{eqnarray}$$

よって、
$$v_t=v_0+at\tag{1-3}\label{p1125eq1-3}$$

　ここで少し気持ち悪い表現がありました。$t=t$ とか、$v=v_0$ とかです。特に $t=t$ が気持ち悪いと思いますが、これは、左側の $t$ は変数としての、もしくは単に「時刻が」という表現をしているもので、右側の $t$ は今考えている時刻 $t$ を表現しています。なので、$t=t$ は「時刻が$t$」というような気持ちです。

その説明を聞けば $v=v_0$ の気持ち悪さは少し薄れましたか？ つまり同様に左側の $v$ は変数としての、もしくは単に「速度が」という表現をしているもので、右側の $v_0$ はその時の実際の速度を表しています。なので、$v=v_0$ は「速度が $v_0$」というような気持ちです。

　もう一つ、気持ち悪いところがありましたか？ 右辺の式変形でしょうか。つまり、
$$\displaystyle\int_{t=0}^{t=t}\displaystyle\frac{dv}{dt}dt = \displaystyle\int_{v=v_0}^{v=v_t}\, dv$$
のところ。右側の方の $\displaystyle\int_{v=v_0}^{v=v_t}\, dv$ は、形式的には $\displaystyle\frac{dv}{\cancel{dt}}\cancel{dt}$ のような気持ちで $dt$ が約分された形で $dv$ だけが残っています。それにより、積分する値が $t=0$ や $t=t$ から $v=v_0$ や $v=v_t$ に変化しています。これでピンときた人は鋭いです。そうです。これは、積分の変数変換をしているのです。積分の変数変換は【置換積分#2】なぜ置換するとうまく積分できるのかで詳しく扱っています。

速度 $v$ から変位 $s$ を導出

速度は
$$v=\frac{ds}{dt}\tag{2-1}\label{p1125eq2-1}$$
より、両辺を $t$ で $t=0$ から $t=t$ まで積分すると、
$$\int_0^t v\, dt=\int_0^t\frac{ds}{dt}dt\tag{2-2}\label{p1125eq2-2}$$

$v$ は式$\eqref{p1125eq1-3}$にて
$$v=v_0+at$$
と求められているからこれを左辺に代入して計算すると

$$\begin{eqnarray} \mathrm{左辺}&=&\displaystyle\int_0^t(v_0+at)\, dt\\ &=&\left[v_0t+\displaystyle\frac{1}{2}at^2\right]_0^t\\ &=&v_0t+\displaystyle\frac{1}{2}at^2 \end{eqnarray}$$

一方右辺は、$t=0$ のときの位置を $s=0$、 $t=t$ のときの位置を $s=s$ と置くと、

$$\begin{eqnarray} \mathrm{右辺}&=&\displaystyle\int_{t=0}^{t=t}\displaystyle\frac{ds}{dt}dt\\ &=& \displaystyle\int_{s=0}^{s=s}\, ds=[s]_0^s\\ &=&s \end{eqnarray}$$

よって、
$$s=v_0t+\displaystyle\frac{1}{2}at^2\tag{2-3}\label{p1125eq2-3}$$
なお、変位 $s$ とは 位置 $x$ の変化量なので $s=x_t-x_0$ です。従って式$\eqref{p1125eq2-3}$は
$$x_t=x_0+v_0t+\displaystyle\frac{1}{2}at^2$$
とも書けます。

まとめ

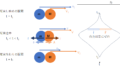
　等加速度運動の3公式を、グラフの傾きや面積を用いながら導くことに加え、微分積分を用いて導きました。その結果として次に示すような関係がイメージできるようになれば目的達成です。