運動量保存の法則は2つの物体間に外力が働いていないという条件をうまく使って運動方程式を解いています。このことにより、衝突問題といった相互に働く力が複雑で求めようのないものでも解くことができます。でも本質は運動方程式を解いているのである、と理解することです。そのことがよくわかる記事も書いています↓ので、そちらもあわせて見てください。
運動量保存の法則
運動方程式を積分して導出
運動量保存の法則は次の式です。
衝突前の運動量の和＝衝突後の運動量の和
$$mv_1+MV_1=mv_2+MV_2$$
この法則を導きます。導く元になるのは運動方程式です。
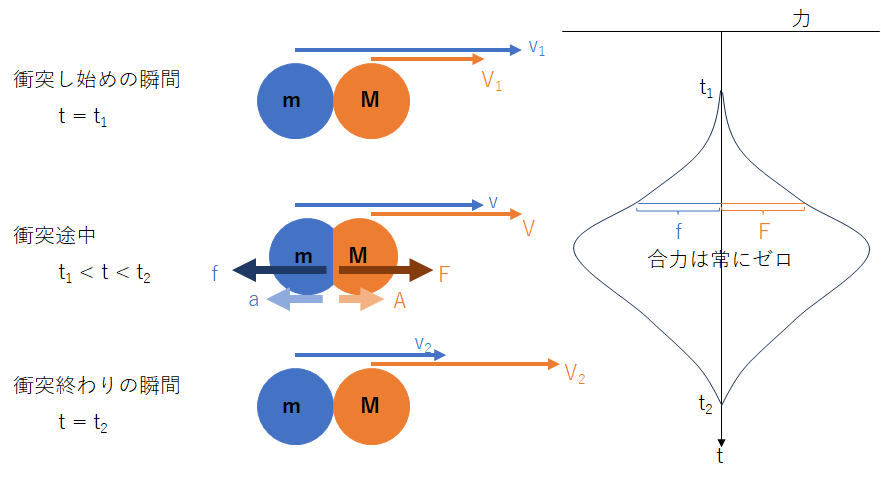
お互いに力が加わっているのは衝突している間だけなので、その間だけを考えます。
運動方程式を立てましょう。力を $f,$ $F$、加速度を $a,$ $A$ と置くと
運動方程式は
\begin{eqnarray}
\left\{ \begin{array}{l}
ma=f\\
MA=F
\end{array}
\right.
\end{eqnarray}
です。加速度 $a$ は $\displaystyle\frac{dv}{dt}$ なのでこの式は次のように書けます。
\begin{eqnarray}
\left\{ \begin{array}{l}
m\displaystyle\frac{dv}{dt}=f\tag{1}\label{p1194eq1}\\
M\displaystyle\frac{dV}{dt}=F
\end{array}
\right.
\end{eqnarray}
ここで、衝突問題における重大な条件を付与します。それは、
衝突している物体間に働く合力はゼロである
という事実です。これは、作用反作用の法則です。この事実を式に表すと
$$f+F=0$$
なので、\eqref{p1194eq1}の上の式と下の式を足すと
$$m\displaystyle\frac{dv}{dt}+M\displaystyle\frac{dV}{dt}=0$$
です。この両辺を衝突している時間 $t=t_1$ から $t=t_2$ で積分すると、
\begin{eqnarray}
左辺&=&m\displaystyle\int_{t=t_1}^{t=t_2}\displaystyle\frac{dv}{\cancel{dt}}\cancel{dt}+M\displaystyle\int_{t=t_1}^{t=t_2}\displaystyle\frac{dV}{\cancel{dt}}\cancel{dt}\\
&=&m\displaystyle\int_{v=v_1}^{v=v_2}dv+M\displaystyle\int_{V=V_1}^{V=V_2}dV\\
&=&m\left[v\right]_{v_1}^{v_2}+M\left[V\right]_{V_1}^{V_2}\\
&=&m(v_2-v_1)+M(V_2-V_1)
\end{eqnarray}
となります。一方、右辺は積分しようが何しようが $0$ なので、この式は
$$mv_1+MV_1=mv_2+MV_2$$
と整理ができます。
なんや！運動方程式そのものやん！！
このように整理した後で運動量保存の法則を再び眺め返してみれば、なんや！運動方程式そのものやん！！と思いませんか？つまり、
$$mv_1+MV_1=mv_2+MV_2$$
を
$$m(v_2-v_1)+M(V_2-V_1)=0\tag{2}\label{p1194eq2}$$
に戻すことにより、
$$m\cdot{dv}+M\cdot{dV}=0$$
つまり、
$$m\displaystyle\frac{dv}{dt}+M\displaystyle\frac{dV}{dt}=0$$
が見えてくれば、式\eqref{p1194eq1}の上下の式を足したに過ぎないと、すなわち外力がゼロの運動系における運動方程式を記述しているに過ぎない、と理解できます。
運動量保存の法則のありがたいところ
運動量保存の法則のありがたいところは、衝突中にどんな力が働いているかを知る必要がない、というところです。同様に衝突時間も知る必要がありません。これは衝突問題がお互いの相互作用だけによるものであり、合力がゼロであるからです。そして衝突している時間も通常はよく分からないわけですが、分からない時間で以てとりあえず積分をしてしまうことにより、力が作用した結果としての速度の変化量が表に現れてきます。速度は我々にとって計測しやすい物理量なので、これに置き換えられることが非常にありがたいところです。
力積について
力積の定義と運動量変化
力 $f$ をある時刻 $t=t_1$ から $t=t_2$ まで物体に加えたとき、その力を時刻で積分した値、すなわち
$$\displaystyle\int_{t_1}^{t_2}f\, dt$$
を力積と定義します。絵で表すと下図のグラフの面積です。
つまり、この物体は力 $f$ を $t=t_1$ から $t=t_2$ までの間受けたことにより、つまり力積を受けたことにより速度が $v=v_1$ から $v=v_2$ に変化した、ということです。
これを式でもう少し明確に表現すれば、式\eqref{p1194eq1}の両辺を時間で積分して、式変形の都合上左辺と右辺を逆にして書くと、
\begin{eqnarray}
\displaystyle\int_{t=t_1}^{t=t_2}f\, dt &=& \displaystyle\int_{t=t_1}^{t=t_2}m\displaystyle\frac{dv}{\cancel{dt}}\cancel{dt}\\
&=&m\displaystyle\int_{v=v_1}^{v=v_2}dv\\
&=&mv_2-mv_1
\end{eqnarray}
です。つまり、与えた力積の量 $\left(\int_{t_1}^{t_2}f\, dt\right)$ だけ運動量が変化する $(mv_2-mv_1)$ ということです。
先ほどは「速度が変化する」と表現しましたが、もちろん質量は不変なのでそれで一向にかまわないのですが、せっかく $mv$ という量が「運動量」と定義されているので、「与えた力積の量だけ運動量が変化する」と表現します。
そしてその力積の量は、青の物体と橙の物体とでは向きが逆で大きさが同じのため、運動量の変化量も向きが逆で大きさが同じであることにより式\eqref{p1194eq2}となり、運動量保存則が成り立つ、というわけです。
スポーツの例
運動量の変化量から力の大きさを想像する：テニスラケットがボールに加える力
このことを利用すると衝突によりどれほどの力が加わっているのかを想像することができます。もちろん正確には力は時刻により刻一刻と変わっていてそれを正確に把握することは容易ではありませんが、そこを大雑把に一定の力がかかっているとして考えます。つまり、下図のように青の部分を面積の等しい緑で置き換えて一定の力 $\bar{f}$ を考えるのです。
例えば、テニスのインパクトではどの程度の力がかかっているのでしょうか。
記事を独立させました。続きはこちら↓をご覧ください。
まとめ
運動量保存の法則を運動方程式から導きました。その際、「外力が働いていない」という条件を用いました。
また、運動方程式は各瞬間瞬間に成り立つ式ですが、瞬間の振る舞いには興味がなく衝突しきった結果だけに興味があるので、その間をすっ飛ばすために積分をしています。
このように、公式の導出過程を見ることで公式が成り立つ条件（外力が働いていないこと）や注目点（瞬間の振る舞いではなく結果の振る舞いに注目していること）が浮き彫りになり、また同時に結局は運動方程式を解いているに過ぎないという安心感も得られます。
実際、運動方程式を愚直に解けば同じ結果は得られます。その例は↓の記事にて述べましたのでぜひそちらも確認ください。
コメント