【運動量保存の法則】ツィオルコフスキーのロケット方程式

　ロケットは燃料を後方に勢いよく噴射することで推進します。すなわち、運動量保存の法則に従って推進します。

24年度の共通テストでこれを取り扱った問題が出ました。ここでは共通テストよりも一歩も二歩も踏み込んで、でも分かりやすく解説します。

直接該当箇所に行きたい場合はこちら。

ロケットの推進は運動量保存の法則

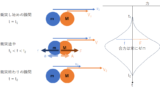
質量：$m$
速度：$V$
短い時間の間に微小燃料 $\Delta m$ を相対速度 $v$ で噴射
このとき、ロケットの速度増加量 $\Delta V$ を求めよ。

空気抵抗や重力は無いとする。

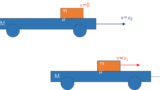
運動量保存の法則より、

$$mV=(m-\Delta m)(V+\Delta V) + \Delta m(V-v)$$

展開して整理すると、
$$\cancel{mV}=(\cancel{m}-\cancel{\Delta m})V+(m-\Delta m)\Delta V+\Delta m(\cancel{V}-v)\tag{1}\label{p1194eq2-1}$$

$$\therefore\; \Delta V=v\frac{\Delta m}{m-\Delta m}\tag{2}\label{p1194eq2-2}$$

　運動量保存の法則は↓の記事で詳しく扱っていますので、復習にどうぞ。

　答えの式を微分方程式の形に書きます。式\eqref{p1194eq2-1}の $\Delta m\Delta V$ を2次の微小量として無視すると式\eqref{p1194eq2-2}は

$$\Delta V = v\frac{\Delta m}{m}$$

となりますから、微分方程式は

$$dV = -v\frac{\, dm}{m}$$

となります。右辺に負号をつけているのは、$\Delta m>0$ ($\Delta m$ は噴射する燃料の質量と置いたため正)に対して $dm<0$ ($m$ 自体はロケットの質量のためその変化量 $dm$ は負)だからです。

これを積分して、

$$\int_{V=V_0}^{V=V_f}dV = -v\int_{m=m_0}^{m=m_f}\frac{1}{m}\, dm$$

\begin{eqnarray}
V_f-V_0 &=& -v(\log{m_f}-\log{m_0})\\
&=& v\log{\frac{m_0}{m_f}}\tag{3}\label{p1194eq2-3}
\end{eqnarray}

となります。

　この式\eqref{p1194eq2-3}の意味は、

は、

で求められることを示しています。

　ここではJAXAの工作ページに載っているデータを引用して説明します。

通常のロケットでは

とのことなので、ロケットの打ち上げを想定すると $V_0=0$ として、

\begin{eqnarray}
V_f &=& 3430\times\log\frac{1}{0.2}\\
&=& 5520\,\mathrm{[m/s]}
\end{eqnarray}

となります。

第1宇宙速度(人工衛星が地球の地表すれすれに飛んだ時に人工衛星になるために必要な速度)は $7.9\mathrm{[km/h]}$ なので、これでは宇宙に飛び立てません。そのため、実際には多段ロケットにしています。

　ツィオルコフスキーのロケット方程式を、運動量保存の法則を立てて積分することで導きました。一見難しそうな工業製品も、原理原則的には結構身近な物理で理解できてしまうことに驚きと親近感を感じますよね。