積の微分を図形で理解する：互い違いの微分の正体は展開公式 ad+bc だった

積の微分公式は、微分が互い違いに出てくるため、最初は「なぜこうなるの？」とモヤモヤしがちです。しかし、展開公式のイメージを使うと、この互い違いがとても自然に理解できます。

結論から言うと、積の微分公式

$$(f(x)g(x))^\prime = f^\prime(x)g(x) + f(x)g^\prime(x)$$

は、展開公式

$(a+b)(c+d)=ac+$ $ad+bc$ $+bd$$

のうち、$ad+bc$ に対応しています。この記事では、この「互い違い $＝ad+bc$」のイメージを、図とアニメーションを使って直感的に理解していきます。

なお、合成関数の微分（連鎖律）も「変化の組み合わせ」を扱う点で近しいテーマです。この記事のあとに読むと理解が深まります。

積の微分公式と展開公式の関係

積の微分を理解するためには「微小変化で積がどう変わるか」を見ます。すなわち、$x$ が微小距離 $dx$ 進んだ時に $y=f(x)g(x)$ がどれだけ進むか を見ます。下図を見て分かる通り、

$dy=(f+df)(g+dg)-fg\tag{1}\label{eq1}$

が $y$ の増加量です。

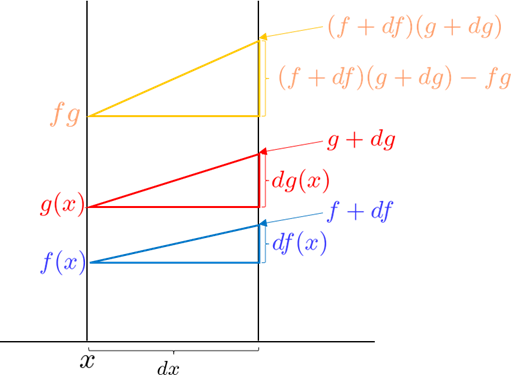
これはまさに、展開公式の形そのものです。展開すると、

$df\cdot g + f\cdot dg$ $+ df\cdot dg$

が現れます。このうち、$df\cdot g + f\cdot dg$ が「互い違い」の正体であり、$ad+bc$ に対応します。

では、このイメージを具体例でつかんでいきましょう。

具体例で理解する：$f(x)=x$, $g(x)=x^2$ の場合

まずは具体例として、

• $f(x)=x$ (青)
• $g(x)=x^2$ (赤)

を考えます。積は $h(x)=x^3$ (黄) なので、微分は $3x^2$ と分かっていますが、ここではあえて「積の微分の仕組み」を見るために分けて考えます。

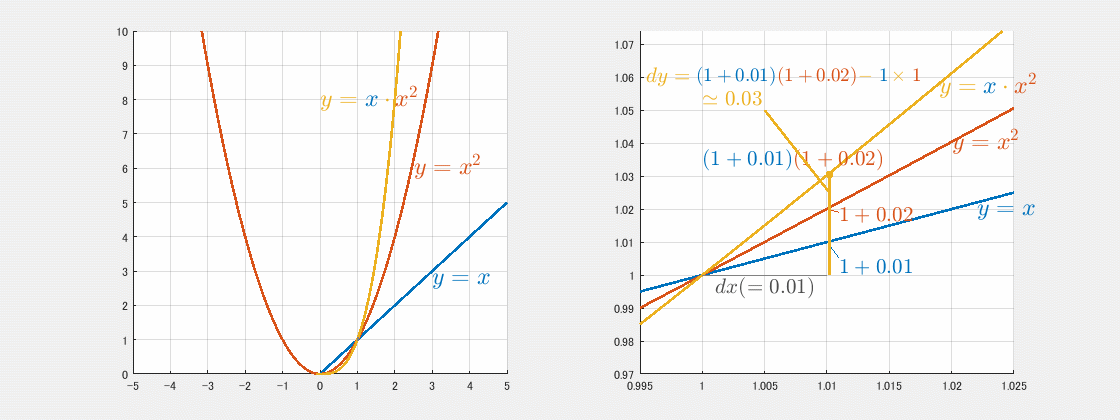
特に $x=1$ の近くを超拡大して、微小変化を観察します。

青の傾きは $1$、赤の傾きは $2$ なので、$dx=0.01$ 進むと $y$ の値は、

• 青：$1+0.01$
• 赤：$1+0.02$

となります。すると積（黄）は、

$(1+0.01)$$(1+0.02)$

です。元の値 $1\times1$ を引けば、増分 $dy$ が求まります。

$$dy=(1+0.01)(1+0.02)-1\times 1$$

展開すると、

\begin{eqnarray} dy &=& 0.03 + 0.01\times0.02 \\ &\simeq& 0.03 \end{eqnarray}

ここで $0.01\times 0.02$ は非常に小さいため無視します。

$dx=0.01$ だったので、

となり、確かに $h'(1)=3$ と一致します。

具体例により式変形の意味を理解したところで、もう一度抽象化して一般形に戻します。

抽象化して一般の形に戻す

$$dy=(f+df)(g+dg)-fg\tag{1:再掲}$$

を展開すると、

$dy =$ $df\cdot g + f\cdot dg$ $+$ $df\cdot dg$

具体例でも確認しましたが、$df\cdot dg$ は無視できるほど小さいので、

$dy \simeq$ $df\cdot g + f\cdot dg$

となります。これがまさに、展開公式の $ad+bc$ に対応する部分です。

両辺を $dx$ で割ると、

\begin{eqnarray} \frac{dy}{dx} &=& \frac{df}{dx}g + f\frac{dg}{dx} \\ &=& f^\prime(x)g(x) + f(x)g^\prime(x) \end{eqnarray}

となり、積の微分公式が現れました。

定義式からの証明

最後に、微分の定義式からも確認しておきます。ここでは、0 を足すテクニックを使います。

• $f(x+h)g(x)-f(x+h)g(x)$

という「0」を足すことで、$\lim$ の中を2つに分けられます。

まとめ

積の微分公式は、展開公式の $ad+bc$ に対応しています。微小変化を使うと、

$$dy = (f+df)(g+dg)-fg$$

を展開し、$df\cdot dg$ を無視することで、互い違いの形が自然に現れます。

定義式からの証明でも、0 を足すことで積が2つに分かれ、同じ形が現れました。

積の微分公式が「なぜ互い違いなのか？」というモヤモヤが、展開公式のイメージでスッキリ晴れていれば嬉しいです。