過去問は「解いて終わり」ではなく、繰り返し解いて実力をつける教材です。本番の共通テストでは丁寧な誘導がついていますが、ここではあえて誘導を省き、自分で見通しを立てる練習ができるようにしています。このような工夫は本ページ独自です。自分で見通しが立てられるようになると、誘導は “高みの見物” になり、余裕を持って解けるようになります。
II.B.C_第1問:三角関数
この問題は、式をいじる前に “イメージで理解する” ことが本質です。単位円で考えると、「$\sin x$ は $y$ 座標」です。
$0\le\theta<\pi$ のとき、方程式
$$\sin\left(\theta+\frac{\pi}{6}\right)=\sin 2\theta\tag{1}\label{p6944eq1}$$
を解け。
共通テストの誘導
実際の共通テストでは、かなり丁寧な誘導がついています。ここではその“エッセンス”だけを示しますので、ヒントとして活用しながら解いてみてください。
まず、左辺と右辺の $\sin$ の中身を $\alpha$, $\beta$ と置きます。
すなわち、$\alpha=\theta+\displaystyle\frac{\pi}{6}$, $\;\beta = 2\theta$ とおくと、式\eqref{p6944eq1}は
$$\sin\alpha=\sin\beta\tag{2}\label{eq2}$$
となります。
(i) 当然、$\alpha=\beta$ なら $\sin\alpha=\sin\beta$ です。
(ii) もう一つの解は、$\alpha+\beta$ を考えよ、と言っています。
解イメージ
同時に、解のイメージも持っておきたいです。
$\sin\alpha=\sin\beta$ とは、単位円上で $y$ の値が同じになるところです。
つまり、次のように視覚的に理解できます。
解
(i) $\alpha=\beta$
最初に $\sin\alpha=\sin\beta$ になるのは図の状態です。つまり、$\alpha=\beta$ のとき。
$$\theta+\frac{\pi}{6}=2\theta$$
$$\therefore\;\theta=\frac{\pi}{6}$$

(ii) $\alpha+\beta=\pi$
次に $\sin\alpha=\sin\beta$ になるのは $\alpha+\beta=\pi$ のとき。
$$\theta+\frac{\pi}{6}+2\theta=\pi$$
$$\therefore\;\theta=\frac{5\pi}{18}$$

(iii) $\alpha+\beta=3\pi$
さらに $\sin\alpha=\sin\beta$ になるのは $\alpha+\beta=3\pi$ のとき。
$$\theta+\frac{\pi}{6}+2\theta=3\pi$$
$$\therefore\;\theta=\frac{17\pi}{18}$$

II.B.C_第3問:微分積分
この問題は、与えられている条件を満たすグラフというのがどういうものかをイメージできるかどうかがミソです。条件を色分けするので、その条件を満たすグラフをイメージしてみてください。
$k$ を $0$ でない実数とし、$f(x)$ を2次関数とする。$F(x)$ と $G(x)$ はどちらも導関数が $f(x)$ であるような関数で、$F(x)$ は $x=0$ で極小値 $0$ をとり、$G(x)$ は $x=k$ で極大値 $0$ を取るとする。
(1) まず、$F(x)=2x^3+3x^2$ の場合を考える。このとき、$F(x)$ と $G(x)$ のグラフを書け。
(2) 次に、$k>0$ の場合を考える。このとき、$F(x)$ と $G(x)$ のグラフの概形を書け。
解イメージ
(1) $G(x)$ は $F(x)$ の上下さまよい版:導関数が同じなので
$F(x)=2x^3+3x^2=x^2(2x+3)$ は、簡単にグラフが描けます。
$G(x)$ のグラフは $F(x)$ を上下に移動したものです。($\because$ 導関数が同じ)
そして、$G(x)$ の極大値は $0$ ということから、$G(x)$ のイメージは次のようになります。
(2) $k>0$ なので極大は正の部分:一方で極小は $x=0$
今度は $k>0$ と指定されています。つまり、$G(x)$ は ($F(x)$ も) 正の部分で極大値をとります。
かつ、「$F(x)$ の極小値は $x=0$ のとき」と指定されているので、
この両者を満たす $F(x)$ の概形は次のようになります。

解
(1)
導関数は
$$ f(x)=6x^2+6x=6x(x+1) $$
より、$x=-1$ で極大値をとり、
$$ F(-1)=2(-1)^3+3(-1)^2=1 $$
よって $F(x)$ のグラフは次のようになる。

$G(x)$ と $F(x)$ の導関数は同じことから、$G(x)$ は $F(x)$ を上下に平行移動したもの。
$G(x)$ の極大値が $0$ ということから、グラフは次のようになる。

(2)
$F(x)$ は $x=0$ で極小、$x=k>0$ で極大となるため、概形は次のようになる。

$G(x)$ の極大値は $0$ より、$G(x)$ のグラフは次のようになる。

II.B.C_第7問:複素数平面
垂直条件を複素数平面上でどのように記述するのか、がミソです。誘導問題に乗れば気づくように作られています。なお、問題文を読みやすくするために、(1)~(3)の共通部分は省略しています。
$\alpha$, $\beta$, $\gamma$ を異なる複素数とし、複素数平面上に3点 $\mathrm{A}(\alpha)$, $\mathrm{B}(\beta)$, $\mathrm{C}(\gamma)$ をとる。また、$z$ は $0$, $2$, $-2$ でない複素数とする。次のような点 $z$ 全体を複素平面上に図示せよ。
(1) $\alpha=z$, $\beta=2$, $\gamma=\displaystyle\frac{4}{z}$ とするとき、
直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わるような点 $z$。
(2) (1)の $\alpha$, $\beta$, $\gamma$ をそれぞれ $-1$ 倍した複素数
$\alpha^\prime = -z$, $\beta^\prime=-2$, $\gamma^\prime=-\displaystyle\frac{4}{z}$ とするとき、
直線 $\mathrm{A^\prime B^\prime}$ と直線 $\mathrm{A^\prime C^\prime}$ が垂直になるような点 $z$。
(3) (1)の $\alpha$, $\beta$, $\gamma$ における $z$ を $-z$ に置き換え
$\alpha^{\prime\prime} = -z$, $\beta^{\prime\prime}=2$, $\gamma^{\prime\prime}=-\displaystyle\frac{4}{z}$ とするとき、
直線 $\mathrm{A^{\prime\prime} B^{\prime\prime}}$ と直線 $\mathrm{A^{\prime\prime} C^{\prime\prime}}$ が垂直になるような点 $z$。
共通テストの誘導
垂直条件:$\omega+\overline{\omega}=0$
この問題に入る前に、次のような誘導問題が置かれています。
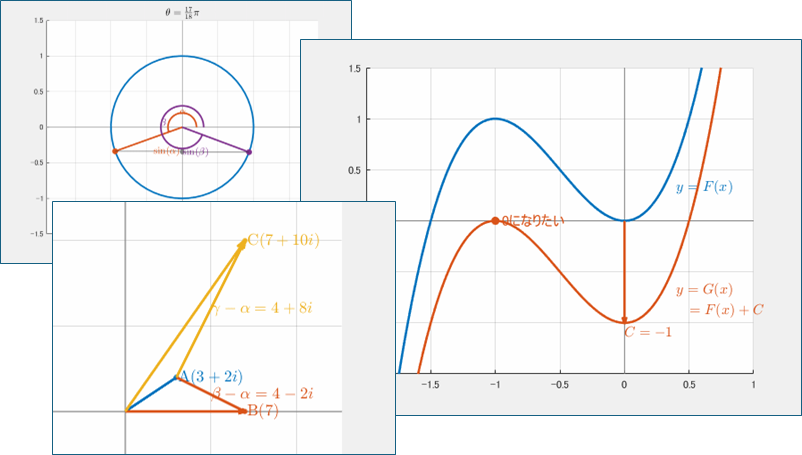
$\alpha=3+2i$, $\beta=7$, $\gamma=7+10i$ のとき、$\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}$ の偏角を求めよ。
$\omega=\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}$ とおく。直線 $\mathrm{AB}$ と直線 $\mathrm{AC}$ が垂直に交わるのは、
$$\omega+\overline{\omega}=[\;\;\;]$$
のときである。
- $\gamma-\alpha =4+8i$
- $\beta-\alpha=4-2i$
であり、この両者は垂直です。誘導に乗って $\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}$ を計算すると、
$$\frac{\gamma-\alpha}{\beta-\alpha} =\frac{(7+10i)-(3+2i)}{7-(3+2i)} =\frac{4+8i}{4-2i} =\frac{40i}{20} =2i$$
割り算をして純虚数になるので垂直です。
参考記事:
このとき $\omega=2i$ なので $\overline{\omega}=-2i$、よって垂直条件は、
$$\omega+\overline{\omega}=0$$
参考記事:
解
(1)
$$\omega=\frac{\gamma-\alpha}{\beta-\alpha} =\frac{\frac{4}{z}-z}{2-z}\cdot\frac{z}{z} =\frac{4-z^2}{z(2-z)} =\frac{(2+z)}{z} =1+\frac{2}{z}$$
垂直条件は、
$$\left(1+\frac{2}{z}\right)+\overline{\left(1+\frac{2}{z}\right)}=0$$
これを整理すると、
\[ 2+\frac{2}{z}+\frac{2}{\overline{z}}=0 \]
両辺に $z\overline{z}$ をかけて整理すると、
\[ (z+1)\overline{(z+1)}=1 \]
よって、
$$|z+1|=1$$
中心 $(-1,0)$、半径 $1$ の円。ただし $(-2,0)$, $(0,0)$ は除く。

(2)
$$\omega=\frac{\frac{4}{-z}-(-z)}{-2-(-z)}\cdot\frac{z}{z} =\frac{-4+z^2}{z(z-2)} =\frac{z+2}{z} =1+\frac{2}{z}$$
(1) と同じ式になります。
したがって、答えも同じく中心 $(-1,0)$、半径 $1$ の円(ただし $(-2,0)$, $(0,0)$ を除く)。

なぜ同じになった?
(1) と (2) の $\omega$ を見比べると、分子分母に $-1$ をかけただけで同じ式になるためです。
(3)
$$\omega=\frac{\frac{4}{-z}-(-z)}{2-(-z)}\cdot\frac{z}{z} =\frac{z^2-4}{z(z+2)} =\frac{z-2}{z} =1-\frac{2}{z}$$
垂直条件は、
$$\left(1-\frac{2}{z}\right)+\overline{\left(1-\frac{2}{z}\right)}=0$$
整理すると、
\[ (z-1)\overline{(z-1)}=1 \]
よって、
$$|z-1|=1$$
中心 $(1,0)$、半径 $1$ の円。ただし $(2,0)$, $(0,0)$ は除く。

まとめ
共通テストの数学は、丁寧な誘導に乗れば確実に得点できるように作られています。まずは誘導の前半部分をしっかり取りにいき、流れに素直に従いながら解いていくことが大切です。
一方で、復習の段階では「誘導なしでどこまで見通しを立てられるか」を意識すると、理解が一段深まります。本ページではそのために、あえて誘導を省き、イメージや本質に立ち返る構成にしています。
三角関数・微分積分・複素数平面という典型分野を通して、“なぜそうなるのか” を自分でつかむ練習ができるはずです。繰り返し解くことで、誘導がなくても自然と見通しが立つようになります。
この記事が、あなたの理解を支え、次の問題への自信につながれば嬉しいです。




コメント