空間の直線の表し方(基礎編)では、 「基準点+$t$×方向ベクトル」 という直線の型を学びました。
また、2次元で $t$ を消去して軌跡方程式を作る流れ(超基礎編)では、 $t$ が “位置を表すパラメータ” であること を確認しました。
この記事では、その考え方をさらに発展させて、 内分点・外分点をベクトル方程式で統一的に扱う方法 を見ていきます。
公式を覚えなくても、 ベクトル方程式だけで位置が求まる という気持ちよさを体験できます。
空間の直線の表し方(基礎編):
2次元で $t$ を消去して軌跡方程式を作る流れ(超基礎編):
1. 内分点の基本
内分点の公式としてよく見る次の式:
$$\overrightarrow{\mathrm{OP}}=(1-t)\,\overrightarrow{\mathrm{OA}}+t\,\overrightarrow{\mathrm{OB}}\tag{1}\label{p8553eq1}$$
実はこれもベクトル方程式です。
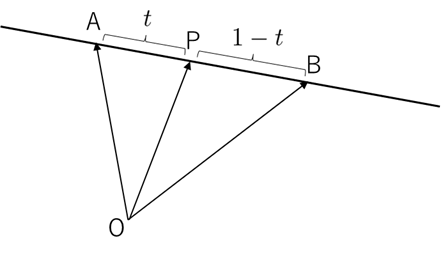
直線上の点を「基準点+t×方向ベクトル」で表しているだけなのです。
1-1. 内分点の式とベクトル方程式
内分点の式を変形してみましょう。
$$\overrightarrow{\mathrm{OP}}=(1-t)\,\overrightarrow{\mathrm{OA}}+t\,\overrightarrow{\mathrm{OB}}\tag{1:再掲}$$
これを整理すると、
$$\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OA}}+t\,(\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}})$$
$$\therefore\;\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OA}}+t\,\overrightarrow{\mathrm{AB}}\tag{2}\label{p8553eq2}$$
つまり、内分点の式は
基準点 $\mathrm{A}$ + $t$ × 方向ベクトル $\mathrm{AB}$
というベクトル方程式そのものです。
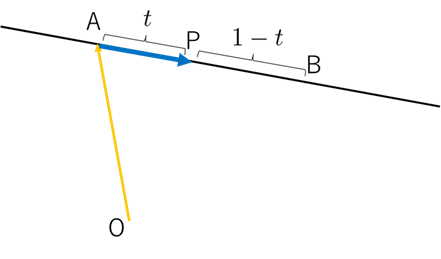
ここでの $t$ は、
点 $\mathrm{P}$ が線分 $\mathrm{AB}$ のどこに位置するかを表す “位置パラメータ” になっています。
この考え方は、後の交点や距離にもそのままつながります。


1-2. 図で理解する内分点
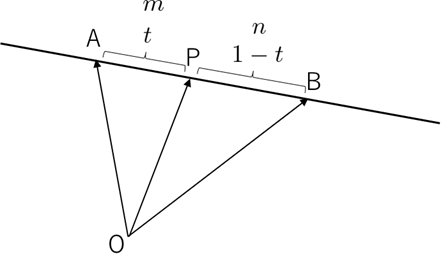
点 $\mathrm{A}$ と点 $\mathrm{B}$ を結ぶ線分の「間」に点 $\mathrm{P}$ があり、比 $m:n$ に応じて位置が決まります。
$m$, $n$ を足して $1$ になるように調整すれば、$t:(1-t)$ です。
式\eqref{p8553eq1}でも式\eqref{p8553eq2}でもどちらでも同じですが、私は式\eqref{p8553eq2}の方が直感的で分かりやすいです。この先、こちらの方で考えていきます。
1-3. 内分点の例題
例題1:A(2,4), B(6,8) を 1:1 に内分する点
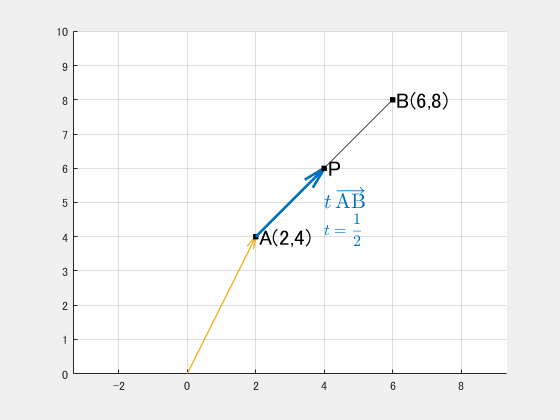
$\mathrm{AB}$ を $1:1$ に内分するということは、
$$t=\frac12$$
です。よって、
\begin{eqnarray}
\overrightarrow{\mathrm{OP}} &=& \overrightarrow{\mathrm{OA}} + \frac12\,\overrightarrow{\mathrm{AB}}\\
&=& \begin{pmatrix}2\\4\end{pmatrix}+\frac12\begin{pmatrix}4\\4\end{pmatrix}\\
&=& \begin{pmatrix}4\\6\end{pmatrix}
\end{eqnarray}
$$\mathrm{P}(4,6)$$
例題2:A(1,2), B(7,5) を 2:1 に内分する点
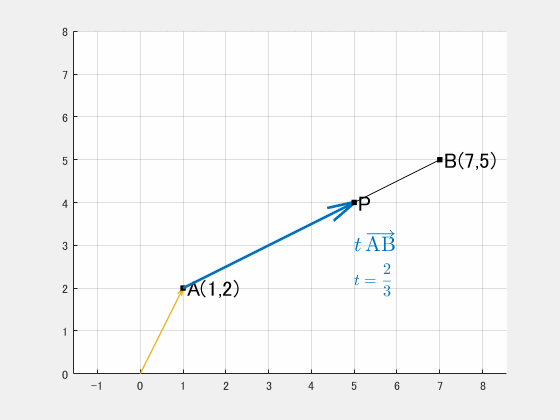
$\mathrm{AB}$ を $2:1$ に内分するということは、
$$t=\frac23$$
です。よって、
\begin{eqnarray}
\overrightarrow{\mathrm{OP}} &=& \overrightarrow{\mathrm{OA}} + \frac23\,\overrightarrow{\mathrm{AB}}\\
&=& \begin{pmatrix}1\\2\end{pmatrix}+\frac23\begin{pmatrix}6\\3\end{pmatrix}\\
&=& \begin{pmatrix}5\\4\end{pmatrix}
\end{eqnarray}
$$\mathrm{P}(5,4)$$
例題3:3次元の内分点 A(1,4,2), B(4,1,5) を 1:2 に内分する点
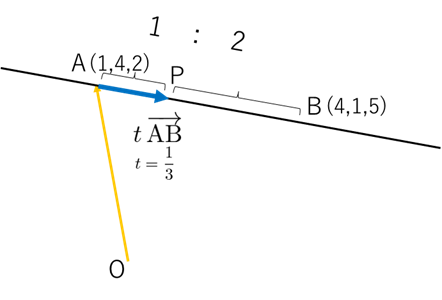
$\mathrm{AB}$ を $1:2$ に内分するということは、
$$t=\frac13$$
です。よって、
\begin{eqnarray}
\overrightarrow{\mathrm{OP}} &=& \overrightarrow{\mathrm{OA}} + \frac13\,\overrightarrow{\mathrm{AB}}\\
&=& \begin{pmatrix}1\\4\\2\end{pmatrix}+\frac13\begin{pmatrix}3\\-3\\3\end{pmatrix}\\
&=& \begin{pmatrix}2\\3\\3\end{pmatrix}
\end{eqnarray}
$$\mathrm{P}(2,3,3)$$
1-4. 図形への応用
図形的な発想(相似など)が思いつかない場合でも、 ベクトル方程式を使えば確実に解ける のが大きな強みです。ここでは、実際の入試問題を ベクトル方程式だけで処理する流れ を見てみましょう。
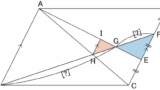
(1) $\mathrm{BG}:\mathrm{GF}$ を求めよ。

基底ベクトルを選ぶ
2次元平面の問題なので、一次独立のベクトルを2つ選べばすべての点は表せます。
ここでは、$\overrightarrow{\mathrm{BA}}$ と $\overrightarrow{\mathrm{BC}}$ としましょう。
そして見やすいようそれぞれ、
- $\overrightarrow{\mathrm{BA}}=\overrightarrow{a}$
- $\overrightarrow{\mathrm{BC}}=\overrightarrow{c}$
と書くことにします。
参考記事:一次独立のイメージ
点G のために直線 BF をベクトル方程式で表す

\begin{eqnarray}
\overrightarrow{\mathrm{BG}} &=& t\,\overrightarrow{\mathrm{BF}}\\
&=& t\,(\overrightarrow{c}+\frac23\overrightarrow{a})\\
&=& \frac23t\overrightarrow{a}+t\overrightarrow{c}
\end{eqnarray}
点G のために直線 AE をベクトル方程式で表す
\begin{eqnarray}
\overrightarrow{\mathrm{BG}} &=& \overrightarrow{\mathrm{BA}}+s\,\overrightarrow{\mathrm{AE}}\\
&=& \overrightarrow{\mathrm{BA}}+s(\overrightarrow{\mathrm{BE}}-\overrightarrow{\mathrm{BA}})\\
&=& \overrightarrow{a}+s(\overrightarrow{c}+\frac13\overrightarrow{a}-\overrightarrow{a})\\
&=& (1-\frac23s)\overrightarrow{a}+s\overrightarrow{c}
\end{eqnarray}
点G は両者の交点
係数を比較して、
\begin{eqnarray}
\left\{\begin{array}{l}
\displaystyle\frac23t=1-\displaystyle\frac23s\\
t=s
\end{array}\right.
\end{eqnarray}
より、
$$s=\frac34,\quad t=\frac34$$
BG:GF=3:1
$t=\displaystyle\frac34$ より、
$$\mathrm{BG}:\mathrm{GF}=3:1$$

上記のような蝶々型の相似が見えれば、実は一瞬で解ける問題ではありました。
しかし、このような図形的な発想が思いつかずともベクトル方程式を使えば解けてしまう、というところが、ベクトル方程式のうれしいところです。
2. 外分点と比較して理解する
外分点とは、点 $\mathrm{A}$ と点 $\mathrm{B}$ を結ぶ直線を延長し、その延長上で $m:n$ に分ける点のことです。
外分点も、実は内分点と同じく 「基準点+$t$×方向ベクトル」 の形で統一的に扱えます。
違いはただひとつ、 $t$ が 0〜1 の範囲を外れる(負になる or 1より大きくなる) というだけです。
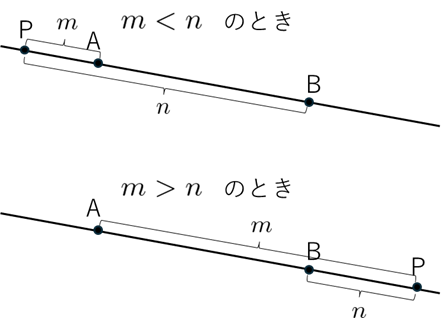
$\mathrm{A}$ から出発し、$\mathrm{P}$ を経由して $\mathrm{B}$ に着く。
$m<n$ であれ $m>n$ であれ、この 一筆書き発想は共通 しています。
外分点の公式:
$$\mathrm{P}=\frac{-nA+mB}{m-n}$$
がありますが、あまり覚える必要はなく、あくまでも\eqref{p8553eq1}ないしは\eqref{p8553eq2}を基本に考えるのがよいです。
2-1. 外分点の例題
例題4:A(2,4), B(10,8) を 1:2 に外分する点
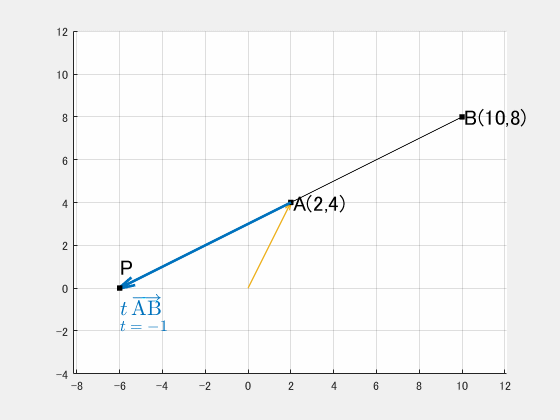
$\mathrm{AB}$ を $1:2$ に外分するということは、
$$t=-1$$
です。よって、
\begin{eqnarray}
\overrightarrow{\mathrm{OP}} &=& \overrightarrow{\mathrm{OA}} – \overrightarrow{\mathrm{AB}}\\
&=& \begin{pmatrix}2\\4\end{pmatrix}-\begin{pmatrix}8\\4\end{pmatrix}\\
&=& \begin{pmatrix}-6\\0\end{pmatrix}
\end{eqnarray}
$$\mathrm{P}(-6,0)$$
2-2. 内分点と外分点の比較図
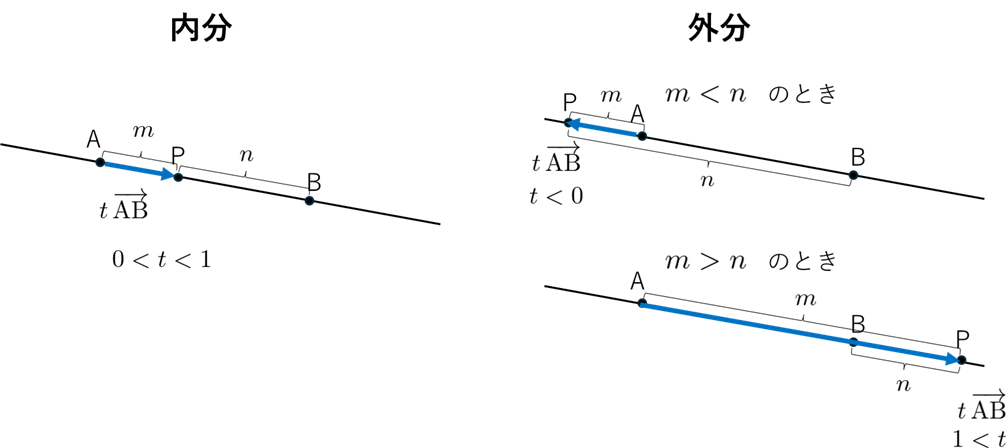
左が内分点、右が外分点です。内分点は線分 $\mathrm{AB}$ の「間」に、外分点は「外側」に位置します。
どちらも「基準点+$t$×方向ベクトル」で表せるため、ベクトル方程式として統一的に扱えます。
3. ベクトル方程式の応用への橋渡し
ここまでで、直線上の点を「基準点+$t$×方向ベクトル」で表す感覚がつかめてきたと思います。
実はこの考え方は、次に扱う平面と直線の交点でもそのまま使えます。
直線をベクトル方程式で表し、その式を平面の方程式に代入すると、パラメータ $t$ を求めるだけで交点や距離が一瞬で求まります。
次の記事では、この方法を使って平面との交点を求める具体例を見ていきましょう。
4. まとめ
- 内分点の式はベクトル方程式と同じ構造
- 外分点も符号が変わるだけで同じ考え方
- 直線上の点は「基準点+$t$×方向ベクトル」で統一的に扱える
- この考え方は平面との交点にも応用できる
次の記事では、この「基準点+t×方向ベクトル」の考え方を使って、 直線と平面の交点を一瞬で求める方法を見ていきます。





コメント