【慶応義塾大学 理工 2024】六面体の空間ベクトル総合問題｜図解で直感！

慶応理工の空間ベクトル問題は、内積・垂線の足・三角形の面積・四面体の体積・内分点と、空間ベクトルの基礎がすべて詰まった総合問題です。図形のイメージとベクトル計算を結びつける練習として最適です。

問題（24年度）

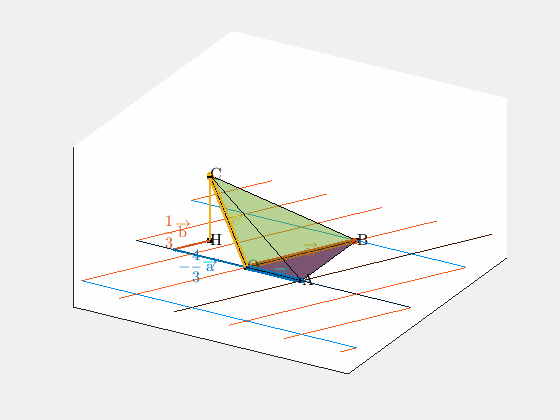
六面体のイメージは次の図のようになります。

(1) 三角形 OAB の面積 → 垂線の足 → 四面体の体積

まずは全体像をアニメーションで確認しておきましょう。

三角形 $\mathrm{OAB}$ の面積

内積を使った面積公式で求められます。

$$S=\frac{1}{2}\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-(\overrightarrow{a}\cdot\overrightarrow{b})^2} =\frac{1}{2}\sqrt{1^2\cdot2^2-1^2} =\frac{\sqrt{3}}{2}\tag{1-1}\label{eq1-1}$$

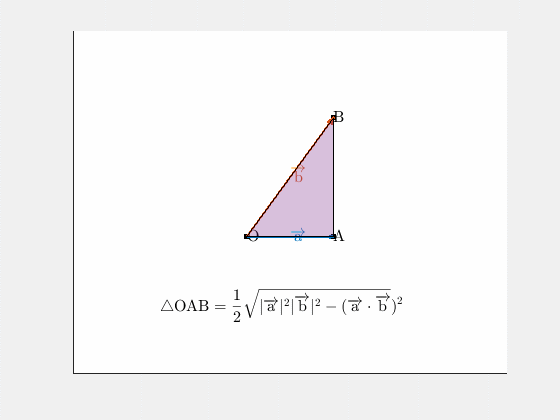
垂線の足 $\mathrm{H}$

平面への垂線の足は、平面上の点までのベクトルと基底ベクトルとの内積ゼロで求めます。

平面上の点までのベクトル

$\mathrm{H}$ は平面 $\mathrm{OAB}$ 上にあるので、

$$\overrightarrow{\mathrm{CH}}=-\overrightarrow{c}+s\,\overrightarrow{a}+t\,\overrightarrow{b}\tag{1-2}\label{eq1-2}$$

基底ベクトルとの内積ゼロ

平面の基底ベクトル $\overrightarrow{a}$, $\overrightarrow{b}$ と内積が $0$ になる条件より、

• $\overrightarrow{\mathrm{CH}}\cdot\overrightarrow{a}=0$ より $1+s+t=0\tag{1-3}\label{eq1-3}$
• $\overrightarrow{\mathrm{CH}}\cdot\overrightarrow{b}=0$ より $s+4t=0\tag{1-4}\label{eq1-4}$

連立方程式を解く

$$s=-\frac{4}{3},\quad t=\frac{1}{3}$$

$\overrightarrow{\mathrm{CH}}$

これを\eqref{eq1-2}に代入すると、

$$\overrightarrow{\mathrm{CH}}=-\frac{4}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}-\overrightarrow{c}\tag{1-5}\label{eq1-5}$$

四面体 $\mathrm{OABC}$ の体積

底面積

$$S=\frac{\sqrt{3}}{2}$$

高さ $|\overrightarrow{\mathrm{CH}}|$

\eqref{eq1-5} を2乗し、与えられた内積を用いると、

$$|\overrightarrow{\mathrm{CH}}|=\frac{2\sqrt{2}}{\sqrt{3}}$$

体積

$$V=\frac13\cdot\frac{\sqrt{3}}{2}\cdot\frac{2\sqrt{2}}{\sqrt{3}}=\frac{\sqrt{2}}{3}$$

(2) 内分点 $\mathrm{I}$, $\mathrm{J}$, $\mathrm{K}$ を使った内積と面積

位置ベクトルは次のように整理できます。

\begin{eqnarray} \overrightarrow{\mathrm{OI}}&=&t\,\overrightarrow{a}\\ \overrightarrow{\mathrm{OJ}}&=&\frac12\overrightarrow{b}\\ \overrightarrow{\mathrm{OK}}&=&\overrightarrow{b}+\frac12\overrightarrow{c}\tag{2-1}\label{eq2-1} \end{eqnarray}

内積 $\overrightarrow{\mathrm{JI}}\cdot\overrightarrow{\mathrm{JK}}$

\begin{eqnarray} \overrightarrow{\mathrm{JI}}&=&t\,\overrightarrow{a}-\frac12\overrightarrow{b}\\ \overrightarrow{\mathrm{JK}}&=&\frac12(\overrightarrow{b}+\overrightarrow{c})\tag{2-2}\label{eq2-2} \end{eqnarray}

計算すると、

$$\overrightarrow{\mathrm{JI}}\cdot\overrightarrow{\mathrm{JK}}=-1$$

三角形 $\mathrm{IJK}$ の面積

\begin{eqnarray}
\triangle\mathrm{IJK} &=& \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{JI}}|^2|\overrightarrow{\mathrm{JK}}|^2-(\overrightarrow{\mathrm{JI}}\cdot\overrightarrow{\mathrm{JK}})^2}\\
&=& \cdots\\
&=& \frac{1}{2}\sqrt{2t^2-2t+1}
\end{eqnarray}

アニメーション解説

全体イメージをアニメーションで確認してみましょう。

アニメーションの「真横からの視点」では、$\mathrm{I}$ から直線 $\mathrm{KJ}$ に下した垂線の足が動かないことが分かります。これが、内積が $t$ によらず一定値 $-1$ になる理由です。

(3) 平面 $\mathrm{IJK}$ が $\mathrm{DE}$ と交わる条件

まずはアニメーションで、平面 $\mathrm{IJK}$ と辺 $\mathrm{DE}$ の位置関係を確認しましょう。

アニメーションより、$\mathrm{DE}$ 上に点が現れる範囲は

$$\frac13\le t<1$$

と分かります。以下ではこれをベクトルで確認します。

方針

点 $\mathrm{P}$ は、

• 平面 $\mathrm{IJK}$ 上の点、かつ
• 線分 $\mathrm{DE}$ 上の点

です。両者のベクトル方程式を連立して求めます。

解答

平面 $\mathrm{IJK}$ 上の点

$$\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OJ}}+p\,\overrightarrow{\mathrm{JI}}+q\,\overrightarrow{\mathrm{JK}}$$

整理すると、

$$\overrightarrow{\mathrm{OP}} = tp\,\overrightarrow{a} + \frac{1}{2}(1-p+q)\,\overrightarrow{b} + \frac{1}{2}q\,\overrightarrow{c} \tag{3-1}\label{eq3-1}$$

ただし、$\mathrm{I}$ は内分点なので $0<t<1$ です。

線分 $\mathrm{DE}$ 上の点

線分 $\mathrm{DE}$ は、

\begin{eqnarray} \overrightarrow{\mathrm{OP}} &=& \overrightarrow{\mathrm{OD}} + k\,\overrightarrow{\mathrm{DE}}\\ &=& \overrightarrow{a} + \overrightarrow{c} + k\,\overrightarrow{b} \quad (0\le k\le 1) \tag{3-2}\label{eq3-2} \end{eqnarray}

交点の条件

$\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$ は一次独立なので、\eqref{eq3-1} と \eqref{eq3-2} の係数を比較します。

\begin{gather}
tp = 1\tag{1}\label{p5728eq1}\\
\displaystyle\frac{1}{2}(1-p+q) = k\tag{2}\label{p5728eq2}\\
\displaystyle\frac{1}{2}q = 1\tag{3}\label{p5728eq3}
\end{gather}

連立方程式を解く

\eqref{p5728eq1} より $p=\dfrac{1}{t}$。

\eqref{p5728eq3} より $q=2$。

これを \eqref{p5728eq2} に代入すると、

$$k=\frac{1}{2}\left(3-\frac{1}{t}\right)$$

$0\le k\le 1$ に注意すると、

$$0\le \frac{1}{2}\left(3-\frac{1}{t}\right)\le 1$$

$$\therefore\; 1\le \frac{1}{t}\le 3$$

$0<t<1$ より、

$$\frac{1}{3}\le t<1$$

まとめ

慶応大学理工2024年度まとめ

慶応大学理工2024年度の空間ベクトル問題は、内積・垂線の足・面積・体積・内分点という基本技術を丁寧に積み上げることで解ける良問でした。六面体のイメージを持ちながらベクトル計算を進めると、空間図形の理解が一気に深まります。

復習におすすめの記事：