二次関数×面積の実戦編です。これまでのページ(パターン整理の #4338、等積変形の基礎 #8102、応用 #8133)で学んだ “発想の型” を、実際の高校入試問題でどう使うかを確認します。
今回扱う3問は、一見すると複雑ですが、どれも「三角形の面積 = 縦の差 × 横の差 × 1/2」や「等積変形」といった基本の型で整理できます。図や動画で状況をつかみながら、入試レベルの問題をスッキリ読み解いていきましょう。
問題1:難問中の基本
放物線 $y=ax^2$($a>0$)上に点 $\mathrm{A}$, $\mathrm{B}$ があり、$x$ 座標はそれぞれ $2,\,-4$。このとき $\triangle\mathrm{OAB}$ の面積は $24$ である。$a$ の値を求めよ。

(23年 東海高校 (1)のみ。一部改変)
イメージ
$a$ が決まれば放物線が決まり、点 $\mathrm{A}$, $\mathrm{B}$ の高さも決まり、$\triangle\mathrm{OAB}$ の面積も一意に決まる──その流れをつかむ問題です。
放物線の形が $a$ で決まるイメージは、下記の基礎記事で扱っています。
解法の要点(発想)
点 $\mathrm{A}$, $\mathrm{B}$ は $y=ax^2$ 上にあるので、
\[ \mathrm{A}(2,4a),\quad \mathrm{B}(-4,16a) \]
次に、直線 $\mathrm{AB}$ の 切片 $\mathrm{P}$ (縦の差) を求める。
切片が分かれば、 $\mathrm{A}$ と $\mathrm{B}$ の $x$ 座標の差 (横の差) により、
$\triangle\mathrm{OAB}=$ 縦の差 × 横の差 × $\displaystyle\frac12$
で一瞬で求められるからです(下記記事の「パターン0」)。
解答
直線 $\mathrm{AB}$ の傾きは
\[ \frac{16a-4a}{-4-2}=\frac{12a}{-6}=-2a \]
よって、直線 $\mathrm{AB}$ の式は
\begin{eqnarray}
y &=& -2a(x-2)+4a\\
&=& -2ax+8a\tag{1-1}\label{eq1-1}
\end{eqnarray}
切片は
$\mathrm{P}(0,8a)$

直線 $\mathrm{AB}$ の切片は $8a$。
点 $\mathrm{A}$ と点 $\mathrm{B}$ の $x$ 座標の差は $6$。
$\triangle\mathrm{OAB}=$ $8a$ $\times$ $6$ $\times\displaystyle\frac12=24a$
これが $24$ なので、
$$a=1$$
補足:面積は「縦の差 × 横の差 × 1/2」
今回のように、切片が分かれば三角形を分割して面積は一瞬です。これは 下記記事の「パターン0」 の基本テクニックです。
また、\eqref{eq1-1}のように直線の式を一行で書く方法は下記で詳しく扱っています。
問題2:(2)は等積変形で計算を楽に
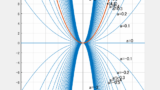
各辺が $x$ 軸・$y$ 軸に平行な正方形 $\mathrm{ABCD}$, $\mathrm{CEFG}$, $\mathrm{FHIJ}$ がある。点 $\mathrm{A}$ は $y$ 軸上にあり、関数 $y=ax^2$, $y=x^2$, $y=\displaystyle\frac{1}{9}x^2$ のグラフは、それぞれ点 $\mathrm{C}$, $\mathrm{F}$, $\mathrm{I}$ を通る。3つの正方形の面積がすべて等しいとき、

(1) $a$ の値を求めよ。
(2) 点 $\mathrm{B}$ を通る傾き $-2$ の直線上にあり、$x$ 座標が正である点 $\mathrm{P}$ について、$\triangle\mathrm{PBJ}$ の面積が四角形 $\mathrm{ABIJ}$ の面積に等しくなるとき、点 $\mathrm{P}$ の座標を求めよ。
(22年 東海高校)
イメージ(前編:正方形が“さまよう”)
(1) $a$ の値を求めよ。
3つの正方形が“同じ面積になる位置”を探して動いているイメージです。面積が等しい正方形なので、すべての辺の長さが等しいことを使います。
解法の要点(前編)
正方形の面積が等しい → 辺の長さが等しい → 点 $\mathrm{C}$, $\mathrm{F}$, $\mathrm{I}$ の $x$ 座標は
$m$, $2m$, $3m$
と置けます。

解答(前編)
点の座標は
$\mathrm{C}($$m$$,am^2)$
$\mathrm{F}($$2m$$,(2m)^2)$
$\mathrm{I}($$3m$$,\displaystyle\frac19(3m)^2)$
正方形なので縦の長さも $m$。よって、
\[ am^2-(2m)^2=m \tag{2-1}\label{eq2-1} \] \[ (2m)^2-\displaystyle\frac19(3m)^2=m \tag{2-2}\label{eq2-2} \]
\eqref{eq2-2} より、
\[ 4m^2-m^2=m\\3m^2-m=0 \]
\[\therefore\;m=\frac13\]
これを \eqref{eq2-1} に代入すると、
\[ \frac19 a – \frac49 = \frac13\]
\[\therefore\;a=7 \]
イメージ(後編:等積変形で三角形を動かす)
(2) 点 $\mathrm{B}$ を通る傾き $-2$ の直線上にあり、$x$ 座標が正である点 $\mathrm{P}$ について、$\triangle\mathrm{PBJ}$ の面積が四角形 $\mathrm{ABIJ}$ の面積に等しくなるとき、点 $\mathrm{P}$ の座標を求めよ。
$\mathrm{ABIJ}$ の面積は計算すれば求められます。
$\triangle\mathrm{PBJ}$ の面積をそれと同じにせよ、という問題ですが、
点 $\mathrm{J}$ のままだと計算が大変なので、
点 $\mathrm{B}$ と同じ $y$ 軸上に移動させ、$\mathrm{J^\prime}$ とします。
解法の要点(後編)
四角形 $\mathrm{ABIJ}$ の面積は
- 底辺:$\mathrm{AB}=m=\displaystyle\frac13$
- 高さ:$\mathrm{I}$ の $x$ 座標 $=3m=1$
\[ \mathrm{ABIJ}=\frac13\times 1=\frac13 \tag{2-3}\label{eq2-3}\]
次に、$\triangle\mathrm{PBJ}$ を等積変形で $\triangle\mathrm{PBJ’}$ に移す。
点 $\mathrm{J’}$ は、点 $\mathrm{J}$ を通る傾き $-2$ の直線と $y$ 軸の交点。
$$\mathrm{J’}\left(0,\frac{22}{9}\right)$$

すると、$\triangle\mathrm{PBJ’}$ の面積は
- 底辺:$\mathrm{J’B}=\displaystyle\frac{22}{9}-\displaystyle\frac79=\displaystyle\frac{15}{9}$
- 高さ:$\mathrm{P}$ の $x$ 座標 $=x$
\[ \triangle\mathrm{PBJ’}=\frac{15}{9}\cdot x\cdot\frac12=\frac56 x \]
解答(後編)
四角形 $\mathrm{ABIJ}$ と等しい \eqref{eq2-3} ので、
\[ \frac56 x=\frac13\\ x=\frac25 \]
点 $\mathrm{P}$ は $y=-2x+\displaystyle\frac79$ 上にあるので、
\[ y=-2\cdot\frac25+\frac79=-\frac{1}{45} \]
$$\mathrm{P}\left(\frac25,\,-\frac{1}{45}\right)$$
補足:等積変形は「高さが同じ → 面積が同じ」
底辺と平行に頂点を動かしても高さは変わらず、面積が一定になります。下記の記事で基礎を丁寧に扱っています。
問題3:(2)は等積変形で計算を楽に
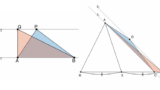
関数 $y=ax^2\,(a>0)$ のグラフ上に点 $\mathrm{A}$ をとる。ただし $\mathrm{A}$ の $x$ 座標は正とする。点 $\mathrm{A}$ を $y$ 軸対称に移した点を $\mathrm{B}$ とすると、$\triangle\mathrm{OAB}$ は 1 辺 1 の正三角形になった。また、$\mathrm{OA}=\mathrm{OC}$ となる点 $\mathrm{C}$ を $y$ 軸の正の部分にとる。このとき、

(1) $a$ の値を求めよ。
(2) 点 $\mathrm{A}$ を通る直線 $l$ によって四角形 $\mathrm{OACB}$ が面積の等しい 2 つの図形に分けられるとき、直線 $l$ と辺 $\mathrm{OB}$ の交点の座標を求めよ。
(21年 東海高校)
イメージ
全体像はこの動画の通り。特に (2) は、問題2と同じく 等積変形 を使うのがポイントです。
解法の要点(前編)
(1) $a$ の値を求めよ。
正三角形 $\triangle\mathrm{OAB}$ の 1 辺が 1 なので、点 $\mathrm{A}$ の位置は「$60^\circ$ の直角三角形」を使えば決まります。

つまり、点 $\mathrm{A}$ の座標は既知となるので、放物線 $y=ax^2$ に代入すれば $a$ が決まります。
解答(前編)
点 $\mathrm{A}$ の座標は
\[ \mathrm{A}\left(\frac12,\;\frac{\sqrt3}{2}\right) \]
これを $y=ax^2$ に代入すると、
\[ \frac{\sqrt3}{2}=a\left(\frac12\right)^2 \\ \therefore\;a=2\sqrt3 \]
解法の要点(後編)
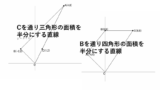
(2) 点 $\mathrm{A}$ を通る直線 $l$ によって四角形 $\mathrm{OACB}$ が面積の等しい 2 つの図形に分けられるとき、直線 $l$ と辺 $\mathrm{OB}$ の交点の座標を求めよ。
四角形 $\mathrm{OACB}$ の面積は、対角線の長さからすぐに求められます。

その半分になる三角形 $\triangle\mathrm{OAD}$ を作りたいのですが、点 $\mathrm{D}$ を直接求めるのは難しいため、後に等積変形 を使うことを念頭にまず $x$ 軸上の点 $\mathrm{D’}$ を求めます。

その後、$\mathrm{D’}$ を $\mathrm{OA}$ に平行に移動させて(等積変形) $\mathrm{OB}$ と交わる点が求める $\mathrm{D}$ です。

解答(後編)
四角形 $\mathrm{OACB}$ の面積は
\[ S_1=\frac12 \]
よって、$\triangle\mathrm{OAD}$ の面積は $\displaystyle\frac14$。
まず、面積を $\displaystyle\frac14$ にする $x$ 軸上の点 $\mathrm{D^\prime}$ を求めると、
\[ \mathrm{D’}\left(-\frac{1}{\sqrt3},\,0\right) \]
これを $\mathrm{OA}$ に平行に移動させ、$\mathrm{OB}$ との交点が求める点 $\mathrm{D}$。
\[ \therefore\;\mathrm{D}\left(-\frac{\sqrt3}{6},\;\frac12\right) \]
補足:等積変形は「高さが同じ → 面積が同じ」
底辺と平行に頂点を動かしても高さは変わらず、面積が一定になります。下記の記事で基礎を丁寧に扱っています。
まとめ
このページでは、二次関数と面積に関する高校入試の良問を通して、発想の“型”を整理しました。特に次の項目は重要ポイントです。
- 縦の差 × 横の差 × 1/2 で三角形の面積を一瞬で求める
- 等積変形で三角形を動かし、計算しやすい位置に移す
これらはすべて、二次関数の面積問題を解く上での “共通言語” です。今回の3問を通して、複雑に見える図形でも、発想の型に落とし込めば整理して考えられることが実感できたはずです。
関連する基礎・応用のページも合わせて読むと、理解がさらに深まります。





コメント