3つの力とは重力・接触・慣性力です。力学において、少なくとも高校物理の力学においてはこの3つの力をマスターし、運動方程式が立てられさえすれば、（＋問題特有の束縛条件があればそれを立てれば）すべての問題は解くことができます。各種保存則を立てることもありますが、それは運動方程式を式変形したものにすぎません。
ここでは、この3つの力の使い方を例題形式で示していくことにより、力を漏れなく楽に書けるようになることを目的にします。その結果として運動方程式がスラスラ立てられます。そのため、問題文はパッと見てわかるようにかなり端折り、記号等もあまり断りなく使います。また、途中の式変形はWolfram Alphaに頼り、端折る場合があります。
また、重力・接触・慣性力を意識するため、力を色分けします。重力を赤で、接触を緑で、慣性力を茶で書きます（一部、見やすさのためにほかの色を使う場合もあります）。
摩擦力の問題：滑っていれば別々に運動方程式を立てる
問題
まずは重力を書きましょう。接触は、mから見ればMだけ、Mから見ればmと地面です。接触のうち、垂直抗力には摩擦力が働くことにだけ、注意。
解
(1)
Mとmを一体としてみた場合にかかる力は下図。($\rightarrow$ 別体としてみた場合は解説参照)
運動方程式は、
$$(M+m)a_1=F_1$$
$$\therefore\, a_1=\frac{F_1}{M+m}$$
(2)
この時にかかる力は下図。($\rightarrow$ 解答としてはここのものがシンプルにはなるが、考え方としては解説の方がシンプル。)
mの垂直方向の力のつり合いより、
$$N_m=mg$$
mの水平方向の運動方程式より、
$$ma_2=\mu_0N_m$$
また、mとMを一体としてみた場合の運動方程式より、
\begin{eqnarray}
(M+m)a_2 = F_2\\
\therefore\, a_2=\frac{F_2}{M+m}
\end{eqnarray}
が導かれるから、これらより
$$\therefore\, \mu_0=\frac{F_2}{(M+m)g}$$
(3)
この時にかかる力は下図。
Mの運動方程式より、
$$Ma_M=F_3-\mu_1mg\quad(\because N_m=mg)$$
mの運動方程式より、
$$ma_m=\mu_1mg\quad(\because N_m=mg)$$
よって、
\begin{eqnarray}
\therefore\left\{\begin{array}{l}
a_M=\displaystyle\frac{F_3-\mu_1mg}{M}\\
a_m=\mu_1g
\end{array}
\right.
\end{eqnarray}
解説
(1)
解答自体は解説の余地はないほど単純だと思いますが、ここでは「重力・接触・慣性力」に慣れるため、あえて別体として扱い、その場合でも同じ結論になることを示します。
かかっている力を図示すると下図です。
これを、物体ごとに分けると下図です。
各物体で運動方程式を立てます。
\begin{eqnarray}
M: \left\{\begin{array}{l}
0=N_M-N_m-Mg\\
Ma_1=F_1-f
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
m: \left\{\begin{array}{l}
0=N_m-mg\\
ma_1=f
\end{array}
\right.
\end{eqnarray}
それぞれの下側の式の和から
$$a_1=\frac{F_1}{M+m}$$
が導かれます。
(2)
解答ではごちゃごちゃと書きましたが、本質は運動方程式を立てることだけです。物体ごとに分けると図は下記のようになります。
ゆえに運動方程式は
\begin{eqnarray}
M: \left\{\begin{array}{l}
0=N_M-N_m-Mg\\
Ma_2=F_2-\mu_0 N_m
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
m: \left\{\begin{array}{l}
0=N_m-mg\\
ma_2=\mu_0 N_m
\end{array}
\right.
\end{eqnarray}
となり、これらから $\mu_0$ を求めたに過ぎない、と理解できればすっきりします。
(3)
これも、力を書いて運動方程式を立てたら終わりと理解できればOKです。物体ごとに分けると図は下記のようになります。
ゆえに運動方程式は
\begin{eqnarray}
M: \left\{\begin{array}{l}
0=N_M-N_m-Mg\\
Ma_M=F_3-\mu_1 N_m
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
m: \left\{\begin{array}{l}
0=N_m-mg\\
ma_m=\mu_1 N_m
\end{array}
\right.
\end{eqnarray}
となり、これらから $a_M$, $a_m$ を求めたに過ぎません。
滑車の問題：複数あると難しいが、一つ一つ丁寧に運動方程式を立てる
問題
まずは重力を書きましょう。接触は、A, B, Cから見れば紐だけ、滑車から見ても紐だけです。
解
この時にかかる力は下図。
上側を正に取って運動方程式を立てると、
\begin{eqnarray}
\left\{\begin{array}{l}
ma=T-mg\\
mb=T-3mg\\
mc=2T-4mg
\end{array}
\right.
\end{eqnarray}
また、A,B,Cは紐と滑車に拘束されていることから、加速度 $a$, $b$, $c$ の間には
$$\frac{a+b}{2}=-c$$
の関係がある。
これらを解いて、
\begin{eqnarray}
\left\{\begin{array}{l}
a=\displaystyle\frac{5}{7}g\\
b=-\displaystyle\frac{3}{7}g\\
c=-\displaystyle\frac{1}{7}g\\
T=\displaystyle\frac{12}{7}mg
\end{array}
\right.
\end{eqnarray}
解説
方程式の解について
Wolfram Alphaで確かめられます。
A+B=C なのに動く違和感について
Aの重さが $m$、Bの重さが $3m$ で、Cの重さはその和である $4m$ なので釣り合って動かないのでは、と思うかもしれませんが、動きます。
簡単な思考実験として、Aの重さをゼロ、Bの重さを $4m$ としてみたらどうでしょうか？ この時も同じように A+B=C の重さの関係にあるにも関わらず、明らかに動きますよね。この思考実験により本問題の状態も動くことが納得できると思います。
滑車について
滑車に書くべき絵は本来は下図です。
しかし、「滑車は軽い」ことから質量がゼロと見なせます。そのため、運動方程式は
$$0\cdot a_{滑車} = T^\prime-2T$$
となるため、$T^\prime=2T$ となります。解答ではここの立式を端折っています。
座標の正の向きについて
これはどちらを正にしてもよいです。なんなら物体A,B,C毎に変えてもよいです。自分で式を立ててみるとすぐに納得できます。
加速度の関係式について
AとBは紐でつながっており、紐は滑車に掛かっています。なので、滑車の変位はAとBの変位の真ん中になるため、
$$\frac{a+b}{2}=-c$$
の関係式が得られます。右辺が $-c$ と、負になっているのは、Cの加速度の向きを上側を正と置いたためです。つまり、A, Bが正の方向に行く場合 $c<0$ とりますが、これはCが下に行くことを表しており、つじつまが合います。
$\displaystyle\frac{a+b}{2}=-c$ を導くには、動滑車に乗った観測者から見て立式してもよいです。その場合は、観測者が $-c$ の加速度で動いているため、観測者から見て
- Aは $a-(-c)$ で近づき
- Bは $(-c)-b$ で遠ざかる
ように見えます。そしてその両者は紐でつながっているため等しく、
$$a-(-c)=(-c)-b$$
と立式できます。符号がややこしいので、Aは上側を正、Bは下側を正、Cは下側を正、と置く方が分かりやすいかもしれないですね。
ばねの問題：左右のばねから受ける力を丁寧に書いてみる
問題
この問題では上下方向は関係ないので重力は考えなくてよいですね。接触は、ばねだけです。
解
(1)
左のばねは自然長から $x_1$ だけ伸びている。右のばねが自然長から $x_2$ だけ伸びているとすると、
$$x_1+x_2=x_0\tag{1}\label{p2411eq1-1}$$
が成り立つ。
この時にかかる力は下図。
すなわち、
$$k_1x_1=k_2x_2\tag{2}\label{p2411eq1-2}$$
が成り立つ。\eqref{p2411eq1-1}, \eqref{p2411eq1-2}より $x_1$, $x_2$ を求めると、
\begin{eqnarray}
\left\{\begin{array}{l}
x_1=\displaystyle\frac{k_2}{k_1+k_2}x_0\\
x_2=\displaystyle\frac{k_1}{k_1+k_2}x_0
\end{array}
\right.
\end{eqnarray}
(2)
釣り合いの位置 $x_1$ からさらに $x$ だけ変位させたときにかかる力は下図。
$k_1x_1$ と $k_2x_2$ は等しいからキャンセルした状態で考えると、運動方程式は
$$ma=-(k_1+k_2)x$$
つまり、$K=k_1+k_2$ のばね定数を持つ単振動となるから、周期 $T$ は、
$$T=2\pi\sqrt{\frac{m}{k_1+k_2}}$$
解説
方程式の解について
Wolfram Alphaで確かめられます。
方程式の解のイメージについて
物理的なイメージで確かめてみます。
仮に $k_2=0$ としてみると、$x_1=0$ となります。
これは、右側のばねがたるんたるんのため、壁を $x$ だけ動かしたところで球は動かないことを表しています。納得感があります。
逆に、$k_2=\infty$ としてみると、$x_1=x_0$ となります。
これは、右側のばねがかちんかちんのため、壁を $x$ だけ動かせばその通りに球が動いてくることを表しています。これも納得感があります。
円運動の問題：エネルギー保存の法則とのコラボ
問題
まずは重力を書きましょう。接触は、糸だけです。
解
角度 $\theta$ における図は下図。
中心方向の運動方程式とエネルギー保存の法則より、
\begin{eqnarray}
\left\{\begin{array}{l}
m\displaystyle\frac{v^2}{l}=T-mg\cos\theta\\
\displaystyle\frac{1}{2}mv_0^2=\displaystyle\frac{1}{2}mv^2+mgl(1-\cos\theta)
\end{array}
\right.
\end{eqnarray}
ここから $v$ を消去して $T$ を求め、その最小値が $0$ 以上であればよいから、
$$T=\frac{mv_0^2}{l}-mg(2-3\cos\theta)\ge\frac{mv_0^2}{l}-5mg\ge 0$$
$$\therefore\, v_0\ge\sqrt{5gl}$$
解説
方程式の解について
Wolfram Alphaで確かめられます。
様々な派生問題について
様々な派生問題が考えられます。
(1) $\theta=\theta_{\mathrm{max}}\le 90^{\circ}$ で静止する場合の張力 $T_1$
$\theta_{\mathrm{max}}$ で一旦静止する。この時の中心方向の運動方程式は
$$m\frac{0^2}{l}=T_1-mg\cos\theta_{\mathrm{max}}$$
$$\therefore\, T_1=mg\cos\theta_{\mathrm{max}}$$
(2) $\theta=120^{\circ}$ で糸がたるむような $v_0$
$\theta=120^{\circ}$ で $T=0$ となるから、
$$T=\frac{mv_0^2}{l}-mg(2-3\cos\frac{2\pi}{3})=\frac{mv_0^2}{l}-\frac{7mg}{2}=0$$
$$\therefore\, v_0=\sqrt{\frac{7}{2}gl}$$
(3) 微小な範囲で振動するときの周期
単振り子の周期なので、
$$\tau=\pi\sqrt\frac{l}{g}$$
慣性力の問題：観測者が動いていたら慣性力を考える
問題
「摩擦力の問題」の(3)を台車Mに乗っている観測者から見て解け。
解
観測者から見たときにかかる力は下図。$a_m^\prime$ は観測者から見た加速度。
運動方程式は
\begin{eqnarray}
M: \left\{\begin{array}{l}
0=N_M-N_m-Mg\\
0=F_3-\mu_1 N_m-Ma_M
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
m: \left\{\begin{array}{l}
0=N_m-mg\\
ma_m^\prime=\mu_1 N_m-ma_M
\end{array}
\right.
\end{eqnarray}
これを $a_M$, $a_m\prime$ について解くと、
\begin{eqnarray}
a_M &=& \frac{F-\mu mg}{M}\\
a_m^\prime &=& \frac{\mu(M+m)g-F}{M}
\end{eqnarray}
$a_m^\prime$ は観測者から見た加速度であることに注意し、これを地面から見た加速度 $a_m$ に直すと、
\begin{eqnarray}
a_m &=& a_M+a_m^\prime\\
&=& \frac{\cancel{F}-\cancel{\mu_1 mg}}{M}+\frac{\mu_1(M+\cancel{m})g-\cancel{F}}{M}\\
&=& \mu_1 g
\end{eqnarray}
よって、
\begin{eqnarray}
\therefore\left\{\begin{array}{l}
a_M=\displaystyle\frac{F_3-\mu_1mg}{M}\\
a_m=\mu_1g
\end{array}
\right.
\end{eqnarray}
解説
運動方程式の解について
Wolfram Alphaで確かめられます。
結局同じ？
はい、運動方程式を見れば明らかなように、「摩擦力の問題」(3)と同じ式です。
この問題ではわざわざ慣性力を持ち出すまでもないと思います。
泣き別れの台車問題：難問だが、丁寧に運動方程式を立てるよい練習
問題
この問題は途中の計算がとてつもなく面倒ですので、途中の計算よりも運動方程式の立式に注力してください。あとは、保存則が確かに成り立っていることをつかんでください。解よりも先に解説を見ても良いです。
まずは重力を書きましょう。そして接触を書きましょう。
(1)の「Mの上から見た場合」では慣性力を使う考え方もできます。
この問題では「速度」と言っていますが、ここではいろいろな見方を試す意味で速度であったり速さであったり混ぜて考えていきます。
解
(1)-1 静止系から見た場合
この時にかかる力は下図。
よって、mとMの運動方程式は、
\begin{eqnarray}
\left\{\begin{array}{l}
ma_x=N\sin\theta\\
ma_y=mg-N\cos\theta\\
MA=N\sin\theta
\end{array}
\right.
\end{eqnarray}
また束縛条件から、
$$\tan\theta=\frac{a_y}{a_x+A}$$
これらを解いて、
\begin{eqnarray}
\left\{\begin{array}{l}
a_x=\displaystyle\frac{Mg\sin\theta}{(M+m)\sin\theta\tan\theta+M\cos\theta}\\
a_y=\displaystyle\frac{(M+m)g\sin\theta\tan\theta}{(M+m)\sin\theta\tan\theta+M\cos\theta}\\
A=\displaystyle\frac{mg\sin\theta}{(M+m)\sin\theta\tan\theta+M\cos\theta}
\end{array}
\right.
\end{eqnarray}
ここで、物体mが $h_1$ だけ落ちるのにかかる時間を $t$ とすると、
$$h=\frac{1}{2}a_yt^2$$
$t\ge 0$ で解くと、
$$t=\sqrt{\frac{2h_1}{a_y}}$$
よって、
\begin{eqnarray}
\left\{\begin{array}{l}
v_x=a_xt=M\cos\theta\sqrt{\displaystyle\frac{2gh_1}{(M+m)(M+m\sin^2\theta)}}\\
v_y=a_yt=\sin\theta\sqrt{\displaystyle\frac{M+m}{M+m\sin^2\theta}\cdot 2gh_1}\\
V=At=m\cos\theta\sqrt{\displaystyle\frac{2gh_1}{(M+m)(M+m\sin^2\theta)}}
\end{array}
\right.
\end{eqnarray}
(1)-2 Mの上から見た場合
$v_x$, $v_y$ を用いて求める
[解] 求める速度 $v$ は、
\begin{eqnarray}
v^2 &=& v_x^2+v_y^2\\
&=& \frac{M^2\cos^2\theta\cdot 2gh_1}{(M+m)(M+m\sin^2\theta)}+\frac{\sin^2\theta\cdot 2(M+m)gh_1}{M+m\sin^2\theta}\\
&=& \frac{M^2+m(2M+m)\sin^2\theta}{(M+m)(M+m\sin^2\theta)}\cdot 2gh_1
\end{eqnarray}
より、
$$v=\sqrt{\frac{M^2+m(2M+m)\sin^2\theta}{(M+m)(M+m\sin^2\theta)}\cdot 2gh_1}$$
Mの上から観測して求める
この時にかかる力は下図。
よって、mとMの運動方程式は、
\begin{eqnarray}
\left\{\begin{array}{l}
0=N+mA\sin\theta -mg\cos\theta\\
ma=mg\sin\theta+mA\cos\theta\\
0=N\sin\theta-MA
\end{array}
\right.
\end{eqnarray}
これらを解いて、
\begin{eqnarray}
\left\{\begin{array}{l}
a=\displaystyle\frac{(M+m)g\sin\theta}{M+m\sin^2\theta}\\
A=\displaystyle\frac{mg\sin\theta\cos\theta}{M+m\sin^2\theta}\\
N=\displaystyle\frac{Mmg\cos\theta}{M+m\sin^2\theta}
\end{array}
\right.
\end{eqnarray}
ここで、mが $h_1$ だけ落ちるのにかかる時間を $t^\prime$ とすると、mはMの上を加速度 $a$ で距離 $\displaystyle\frac{h_1}{\sin\theta}$ だけ移動しているから、
$$\frac{h_1}{\sin\theta}=\frac{1}{2}at^{\prime 2}$$
$$\therefore\; t^{\prime 2}=\frac{2h_1}{a\sin\theta}$$
ゆえに、
\begin{eqnarray}
v^{\prime 2} &=& (at^\prime)^2 = a^2t^{\prime 2} = a\frac{2h_1}{\sin\theta}=\frac{(M+m)g\cancel{\sin\theta}}{M+m\sin^2\theta}\cdot\frac{2h_1}{\cancel{\sin\theta}}\\
&=& \frac{M+m}{M+m\sin^2\theta}\cdot 2gh_1\\
V^2 &=& (At^{\prime})^2 = A^2t^{\prime 2} = \left(\frac{mg\cancel{\sin\theta}\cos\theta}{M+m\sin^2\theta}\right)^2\cdot\frac{M+m\sin^2\theta}{(M+m)g\cancel{\sin\theta}}\cdot\frac{2h_1}{\cancel{\sin\theta}}\\
&=& \frac{m^2\cos^2\theta}{(M+m)(M+m\sin^2\theta)}\cdot 2gh_1
\end{eqnarray}
ここで、$v^{\prime 2}$ はMの上から見た値であることに注意し、静止系から見た場合の速度を $v$ と置くと次の図の関係がある。
余弦定理より、
\begin{eqnarray}
v^2 &=& v^{\prime 2} + V^2 – 2v^\prime V\cos\theta\\
&=& \frac{M+m}{M+m\sin^2\theta}\cdot 2gh_1 + \frac{m^2\cos^2\theta}{(M+m)(M+m\sin^2\theta)}\cdot 2gh_1\\
&&-2\sqrt{\frac{M+m}{M+m\sin^2\theta}\cdot 2gh_1}\sqrt{\frac{m^2\cos^2\theta}{(M+m)(M+m\sin^2\theta)}\cdot 2gh_1}\,\cos\theta\\
&=& \frac{M^2+m(2M+m)\sin^2\theta}{(M+m)(M+m\sin^2\theta)}\cdot 2gh_1
\end{eqnarray}
ゆえに、
Mの上から見たとき
mの速さ： $v^\prime=\displaystyle\sqrt{\frac{M+m}{M+m\sin^2\theta}\cdot 2gh_1}$
Mの速さ： $0$
静止系から見たとき
mの速さ： $v=\displaystyle\sqrt{\frac{M^2+m(2M+m)\sin^2\theta}{(M+m)(M+m\sin^2\theta)}\cdot 2gh_1}$
Mの速さ： $V=m\cos\theta\displaystyle\sqrt{\frac{2gh_1}{(M+m)(M+m\sin^2\theta)}}$
(2)
運動量保存の法則： $0=MV_2+mv_2$
力学的エネルギー保存の法則： $mgh_2=\displaystyle\frac{1}{2}MV_2^2+\displaystyle\frac{1}{2}mv_2^2$
より、
\begin{eqnarray}
V_2 &=& -m\sqrt{\frac{2gh_2}{M(M+m)}}\\
v_2 &=& M\sqrt{\frac{2gh_2}{M(M+m)}}
\end{eqnarray}
(3)
この時にかかる力は下図。
それぞれの運動方程式は、
\begin{eqnarray}
\mathrm{m:}\left\{\begin{array}{l}
0 = N_m-mg\\
ma_3 = -\mu N_m
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
\mathrm{M:}\left\{\begin{array}{l}
0 = N_M-Mg-N_m\\
MA_3 = \mu N_m
\end{array}
\right.
\end{eqnarray}
これらを解いて、
\begin{eqnarray}
a_3 &=& -\mu g\\
A_3 &=& \frac{m}{M}\mu g\\
N_m &=& mg\\
N_M &=& (M+m)g
\end{eqnarray}
従って、$t$ 秒後のmとMの速度 $v(t)$, $V(t)$ は、(2)の解が初速度なので、
\begin{eqnarray}
v(t) &=& v_2 + a_3 t = M\sqrt{\frac{2gh_2}{M(M+m)}}-\mu g t\\
V(t) &=& V_2 + A_3 t = -m\sqrt{\frac{2gh_2}{M(M+m)}}+\frac{m}{M}\mu g t
\end{eqnarray}
mがMと一体になって動くとき、$v(t)=V(t)$ なので、これより $t(>0)$ を求めると、
$$t=\frac{1}{\mu g}\cdot M\sqrt{\frac{2gh_2}{M(M+m)}}$$
この間にm, Mはそれぞれ
\begin{eqnarray}
x_m &=& v_2 t + \frac{1}{2}a_3 t^2\\
&=& \frac{M}{M+m}\frac{h_2}{\mu}\\
x_M &=& V_2 t + \frac{1}{2}A_3 t^2\\
&=& -\frac{m}{M+m}\frac{h_2}{\mu}
\end{eqnarray}
動くから、
$$l=x_m-x_M=\frac{h_2}{\mu}$$
このときの $v$, $V$ は、
\begin{eqnarray}
v=v_2+a_3 t = 0\\
V=V_2+A_3 t = 0
\end{eqnarray}
解説
(1)
力の絵を物体ごとに分けて書く
力の絵を物体ごとに分けて書くと下図です。Mにかかる上下の力はどうせ釣り合っているのでここでは省略しました。
方程式の解について
Wolfram Alphaで確かめられます。
実際の入試問題ではおそらく小刻みに問題を区切り誘導的に導いていくと思いますが、自分の勉強ではこのようなシンプルな問題設定で一気通貫で解いていくと全体像が理解できてよいと思います。一方で方程式を解くのは骨が折れるので、まずは立式に注力し、計算はコンピュータに頼ってよいと思います。計算を自分で行うにしても立式に自信があってこそ迷いなく解けるものですから。
$v^\prime$ の解法について
$V^\prime$ を求めるだけなら $t$ を求めずに直接次のように求めることもできます。
[別解] ここで、物体mが $h$ だけ落ちたときの速さを $v^\prime$ とすると、それはMの上で加速度 $a$ で $\displaystyle\frac{h_1}{\sin\theta}$ だけ移動しているから、
\begin{eqnarray}
v^{\prime 2} &=& 2as\\
&=& 2\cdot\frac{(M+m)g\cancel{\sin\theta}}{M+m\sin^2\theta}\cdot\frac{h_1}{\cancel{\sin\theta}}\\
&=& \frac{M+m}{M+m\sin^2\theta}\cdot 2gh_1
\end{eqnarray}
エネルギー保存の法則について
Mとmが速度を持つのはmが落ちたからです。ここで、Mとmの運動エネルギーを求め、その和が $mgh$ になることを確かめます。
\begin{eqnarray}
\frac{1}{2}MV^2 &=& \frac{1}{2}M\frac{m^2\cos^2\theta}{(M+m)(M+m\sin^2\theta)}\cdot 2gh_1\\
\frac{1}{2}mv^2 &=& \frac{1}{2}m\frac{M^2+m(2M+m)\sin^2\theta}{(M+m)(M+m\sin^2\theta)}\cdot 2gh_1\\
\frac{1}{2}MV^2+\frac{1}{2}mv^2 &=& mgh_1\cdot\frac{Mm\cos^2\theta+M^2+m(2M+m)\sin^2\theta}{(M+m)(M+m\sin^2\theta)}\\
&=& mgh_1\cdot\frac{Mm(1-\sin^2\theta)+M^2+m(2M+m)\sin^2\theta}{(M+m)(M+m\sin^2\theta)}\\
&=& mgh_1\cdot\frac{M^2+Mm\sin^2\theta+Mm+m^2\sin\theta}{(M+m)(M+m\sin^2\theta)}\\
&=& mgh_1
\end{eqnarray}
(2)
方程式の解について
Wolfram Alphaで確かめられます。
(1)との相違について
滑らかな接続部分において力は複雑に変化するため、(2)の状態はもはや等加速度運動ではないです。そのため、(1)の延長では解けません。しかしながら各種保存則は成り立ちます。保存則は等加速度運動を仮定せずに運動方程式を式変形しているためです。この部分について詳しくは↓の記事を参照ください。
(3)
一体になったときに、$v=0$, $V=0$ について
横方向には外力は働いていないため、終始運動量保存の法則が成り立ちます。終始というのは(1)の最初からで、このときmもMも止まっているため、運動量の「始」の値は $0$ であり、どの時刻でも横方向の運動量の合計は $0$ です。従って、一体となった「終」の値は $v=0$, $V=0$ とならざるを得ません。
一体になったときの $l$ について
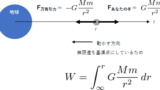
こちらはエネルギー保存の法則が成り立ちます。すなわち、摩擦によってエネルギーが失われますが、失われるエネルギー $W$ は、
\begin{eqnarray}
W &=& \mu N_m\times l\\
&=& \mu mg\times\frac{h_2}{\mu}\\
&=& mgh_2
\end{eqnarray}
となり、最初に持っていた力学的エネルギーがそのまま摩擦エネルギーとして消費されたことを表しています。
おまけ：運動方程式でテニスのスピンを考える
こちらの記事↓ではテニスにおいてスピンをかけて打つことが重要であることを運動方程式を立ててそれをシミュレーションすることで論じています。
コメント