【三平方の定理】手品のように美しい図形証明と、当たり前すぎる数式証明

三平方の定理は、直角三角形の3辺に成り立つ非常に有名な関係式で、高校入試には必ずと言ってよいほど出ます。

この定理の証明にはいくつかの方法がありますが、この記事では

• 図形を使った「手品のように美しい証明」
• 数式を使った「中学生以上なら一瞬で終わる証明」

の2つを紹介します。

証明そのものが入試で問われることは稀ですが、
三平方の定理を使う問題は必ずと言ってよいほど入試に出ます。
証明を知っておくと、定理を使うときの理解が一段深まり、迷いが減ります。

なお、三平方の定理を少し“微調整”した形として 余弦定理 があります。（高校範囲です）

👉 余弦定理はこちら

図形を用いた証明：小学生にも理解できる、手品のようで美しい証明

証明の方針はとてもシンプルで、

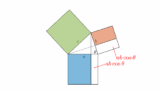
青の面積（$a^2$）＋赤の面積（$b^2$）＝緑の面積（$c^2$）

というものです。

🎥 証明アニメーション

一気に眺めると理解が早いです。再生ボタンを押してください。
面積を保ったまま図形がスルスルと動いていく様子は、まるで手品のようです。

ステップ・バイ・ステップ解説

① 高さが同じなら三角形の面積は等しい

　辺$\mathrm{AD}/\! /$辺$\mathrm{CB}$ なので、
$\triangle\mathrm{ADB}$ と $\triangle\mathrm{ADC}$ の面積は等しいです。

② 回転させても面積は変わらない

$\triangle\mathrm{ADC}$ を回転させると $\triangle\mathrm{ABI}$ になります。

③ 再び、高さが同じなら面積は等しい

辺$\mathrm{AI}/\! /$辺$\mathrm{BJ}$ なので、
$\triangle\mathrm{AIB}$ と$\triangle\mathrm{AIJ}$ の面積は等しいです。

④ 長方形の対角線は面積を半分に分ける

残りの部分も同じ面積になります。

⑤ 赤い部分も同様に変形できる

赤い部分も同じ考え方で変形できます。完成図だけ載せます。

数式を用いた証明：実はこっちの方が圧倒的にシンプル

図形証明は美しいですが、
実際に証明するだけなら 数式の方が圧倒的に簡単 です。

方針は、

同じ面積を別の見方で表す

というものです。

同じ面積を別の見方で表現

　下記のように別の見方をします。

① 左側の面積

一辺が $a+b$ の正方形なので、

$$a^2+2ab+b^2$$

② 右側の面積

中央の正方形（$c^2$）と、
4つの直角三角形（$\frac12 ab$ × 4）から成るので、

$$c^2+2ab$$

③ 両者を等しいと置く

\begin{eqnarray}
a^2+2ab+b^2&=&c^2+2ab\\
\therefore\; a^2+b^2&=&c^2
\end{eqnarray}

まとめ

三平方の定理の証明を、図形と数式の両面から確認しました。

証明そのものが入試に出ることは少ないですが、
三平方の定理を使う問題は入試で必ず出ます。

証明を知っておくと、定理を使うときの理解が深まり、
応用問題でも迷いにくくなります。

---

👉 特殊な三角形（高校入試で頻出）

特殊な直角三角形は特によく出ますので、下記でまとめました。