一次独立と内積が一気にわかる：平面を作る2本のベクトルと射影の直感

ベクトルを学び始めると、いきなり「一次独立」「内積」という言葉が現れて戸惑いがちです。しかしこの2つは、ベクトルの世界を理解するうえで欠かせない基礎です。この記事では、

• 一次独立 ＝ 平面を表現できる2本のベクトル
• 内積 ＝ 角度と影（射影）

という直感的なイメージを、図とアニメーションを使って丁寧に理解します。

一次独立のイメージ

まず結論から言えば、一次独立な2本のベクトルがあれば、平面上の任意の点を表現できます。これは「平面を張る」という性質です。

平面上の任意の点は2つの一次独立なベクトルで表現できる

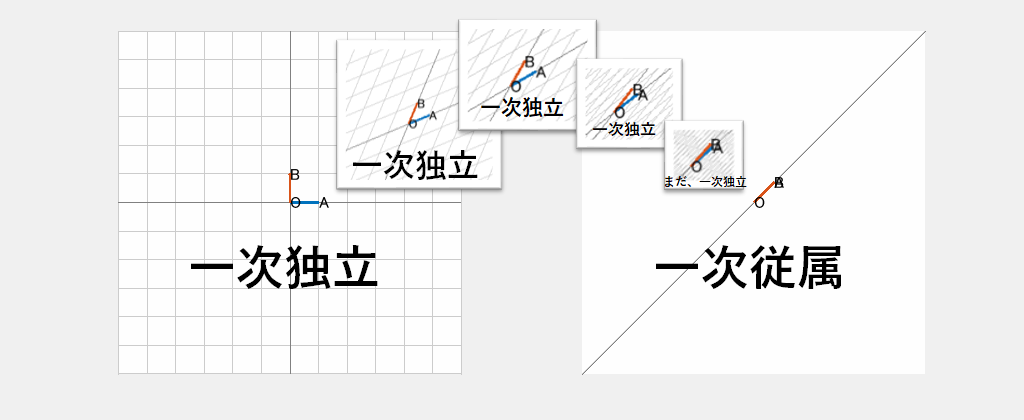
私たちが普段使う座標平面は、下図左のように

$$\overrightarrow{\mathrm{OA}}=\begin{pmatrix}1\\0\end{pmatrix},\quad \overrightarrow{\mathrm{OB}}=\begin{pmatrix}0\\1\end{pmatrix}$$

という2本のベクトルを使って平面を張っています。例えば点 $\mathrm{P}(5,4)$ は、

\begin{eqnarray} \begin{pmatrix}5\\4\end{pmatrix} &=& 5\begin{pmatrix}1\\0\end{pmatrix}+4\begin{pmatrix}0\\1\end{pmatrix}\\ &=& 5\,\overrightarrow{\mathrm{OA}}+4\,\overrightarrow{\mathrm{OB}} \end{eqnarray}

一方、右図のように $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ を別の2本に取り替えても、同じ点 $\mathrm{P}$ を表現できます。

\begin{eqnarray} \begin{pmatrix}5\\4\end{pmatrix} &=& 2\begin{pmatrix}2\\1\end{pmatrix}+1\begin{pmatrix}1\\2\end{pmatrix}\\ &=& 2\,\overrightarrow{\mathrm{OA}}+1\,\overrightarrow{\mathrm{OB}} \end{eqnarray}

このように、2本のベクトルが一次独立である限り、どのように取っても平面全体を表現できます。

ただし例外があります。それは、2本が平行になる場合、またはどちらかが $\overrightarrow{0}$ になる場合です。このときは平面を張れず、表現できるのは直線上の点だけになります。

下のアニメーションは、2本のベクトルが平行でない限りは座標のメッシュが張られ、平面全体を表せることを示しています。しかし最後の瞬間に平行になると、メッシュがつぶれて直線しか表せなくなります。これが「一次従属」です。

空間の場合は3本の一次独立なベクトルが必要です。詳しくは以下の記事で扱っています。

内積の図形的意味

内積とは、「一方のベクトルに、もう一方を投影した長さを掛け合わせたもの」です。ここから角度や垂線の足など、さまざまな図形問題につながります。

$\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}=|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|\cos\theta$

　まずは最もよく使う図形的定義です。

これは角度を求める際に頻繁に使います。

角度問題の例

解

\begin{eqnarray} \cos\theta &=& \frac{\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}}{|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|}\\ &=& \frac{\begin{pmatrix}\sqrt{3}\\1\end{pmatrix}\cdot\begin{pmatrix}1\\\sqrt{3}\end{pmatrix}}{\left|\begin{pmatrix}\sqrt{3}\\1\end{pmatrix}\right|\left|\begin{pmatrix}1\\\sqrt{3}\end{pmatrix}\right|}\\ &=& \frac{2\sqrt{3}}{2\times 2}\\ &=& \frac{\sqrt{3}}{2} \end{eqnarray}

よって、

$$\theta = \frac{\pi}{6}$$

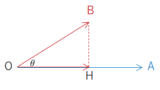
射影としての内積：$\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}=|\overrightarrow{\mathrm{OH}}||\overrightarrow{\mathrm{OA}}|$

内積は「角度」だけでなく、「影（射影）」としても捉えられます。

この見方をすると、$\theta=90^\circ$ のとき内積が $0$ になる理由や、内積の正負の意味が直感的に理解できます。

さらにこの射影の考え方は、垂線の足問題などにも直結します。詳しくは以下の記事で扱っています。

まとめ

一次独立とは「平面（空間）を張るこごができるかどうか」、内積とは「一方のベクトルに、もう一方を投影した長さを掛け合わせたもの」です。

一次独立と内積を理解すると、図形的な関係をすべて数式で表現できるようになります。これにより、図形の問題を計算として処理できるのがベクトルの強みです。
ベクトルがどのように図形を数式化して扱えるのか、その全体像は次の記事でまとめていますので、合わせてご覧ください。