三角関数の加法定理は、数学のさまざまな場面で登場する重要な公式です。しかし、教科書的な証明はどうしても「計算が続くな…」と感じる人も多いはずです。
ところが、複素数の世界に入ると、この公式は驚くほど自然に姿を現します。複素数平面で角度を扱う感覚がつかめていれば、加法定理はむしろ「そうなるよね」と思えるほどシンプルです。
この記事では、複素数の基本性質を使って、三角関数の加法定理を直感的に導いていきます。
三角関数の加法定理とは?
まずはおなじみの公式を確認しましょう。
$\sin(\alpha+\beta) = \sin\alpha\cos\beta+\cos\alpha\sin\beta$
$\cos(\alpha+\beta) = \cos\alpha\cos\beta-\sin\alpha\sin\beta$
角度を分割したり合成したりするときに欠かせない公式ですが、複素数の視点から見るとその構造がとても美しく見えてきます。
複素数平面で考えると何が嬉しいのか?
複素数平面では、
複素数の掛け算=角度の足し算(+拡大縮小)
という性質がありました。この “角度が足される” という性質は、以下の記事で詳しく扱っています。
ここではその性質を使って、三角関数の加法定理をスッと導いていきます。
複素数を掛けると角度が足される
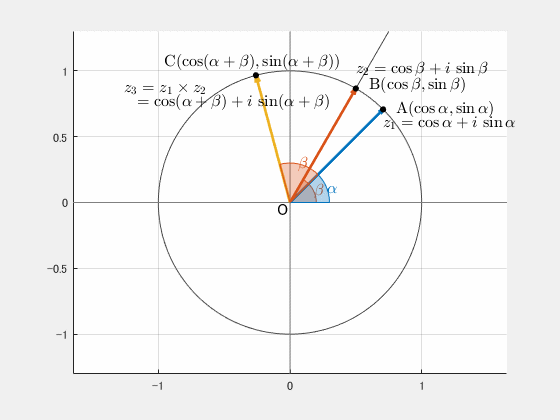
角度 \(\alpha\)、\(\beta\) を持つ複素数を
$z_1=\cos\alpha+i\sin\alpha$
$z_2=\cos\beta+i\sin\beta$
と置き、その積 $z_3=z_1\times z_2$ を考えます。
複素数平面では 掛け算をすると角度が足し合わされる ため、
$$z_3=\cos(\alpha+\beta)+i\sin(\alpha+\beta)$$
となるはずです。
この「角度が足される」イメージ を視覚的に示したのが次の動画です。
動画では、複素数の掛け算が「角度の足し算」として働く様子がつかめるはずです。
あとは展開するだけ
角度が足されることがわかったので、実際に積を展開してみます。
\[ \begin{aligned} \cos(\alpha+\beta)+i\sin(\alpha+\beta) &=(\cos\alpha+i\sin\alpha)(\cos\beta+i\sin\beta)\\ &=\cos\alpha\cos\beta+i\cos\alpha\sin\beta\\ &\quad+i\sin\alpha\cos\beta-\sin\alpha\sin\beta\\ &=\cos\alpha\cos\beta-\sin\alpha\sin\beta\\ &\quad+i(\sin\alpha\cos\beta+\cos\alpha\sin\beta) \end{aligned} \]
実部と虚部を比較すると、最初に示した加法定理がそのまま現れます。
$\sin(\alpha+\beta) = \sin\alpha\cos\beta+\cos\alpha\sin\beta$
$\cos(\alpha+\beta) = \cos\alpha\cos\beta-\sin\alpha\sin\beta$
まとめ
三角関数の加法定理は、複素数の視点から見ると驚くほど自然に導かれます。
・複素数の掛け算は角度を足す
・その性質を使うと、加法定理が一気に見通しよくなる
複素数平面は、三角関数の計算や図形的理解を支える強力な道具です。もっと深く知りたい人は、シリーズの他の記事もぜひどうぞ。


複素数の世界は、知れば知るほど数学のつながりが鮮やかに見えてきます。その楽しさを、これからも一緒に育てていきましょう。

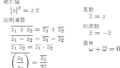
コメント