複素数とは、実数では表しきれない数の世界を広げる魔法のような存在です。数直線上ではなく、複素数平面上で考えることで、その本質が驚くほど明快になります。本記事では、複素数の加減乗除が「座標変換」として解釈できることを通じて、直感的な理解を目指します。
複素数と複素数平面
複素数とは?
複素数は、
$$z=a+bi$$
$a,b$ は実数、$i$ は虚数単位という形で表されます。これは、平面上の座標 $(a,b)$ としても捉えられるため、図形的な視点がとても有効になります。
複素数平面
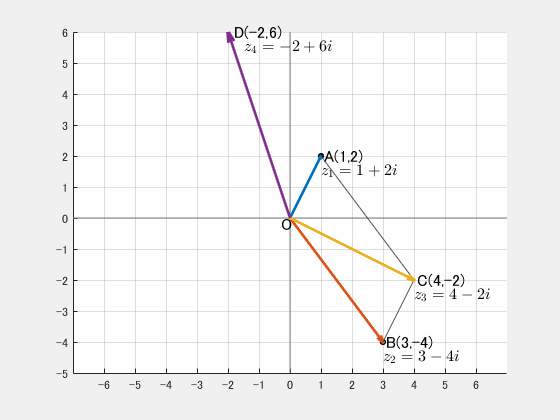
例えば、複素数 $z_1=1+2i$ は複素数平面上では $(1,2)$ に、$z_2=3-4i$ は $(3,-4)$ にプロットされます。

座標変換としての加減乗除
加法と減法:ベクトルの和と差
複素数の加法・減法はベクトルの加法・減法として理解できます。
- 加法: 例として、$z_1 = 1 + 2i$ と $z_2 = 3 – 4i$ を足すと、
$$z_1 + z_2 = (1+3) + (2-4)i = 4 – 2i$$
これは、複素数平面上で両者のベクトルを加えたこと意味します。 - 減法: 同様に、$z_1 – z_2$ はベクトルの差となります。
$$z_1 – z_2 = (1-3) + (2+4)i = -2+6i$$
乗法:順回転と拡大
簡単な例:$i$ を掛けると90度回転
複素数の掛け算は「回転+拡大縮小」という性質を持ちます。
- 乗法の基本: 例えば $i$ を掛けると、
$$(1 + i)\times i = i + i^2 = i – 1 = -1 + i$$
これは、90度反時計回りに回転させる操作です。
ステップ・バイ・ステップで確認します。
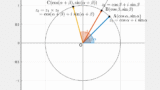
掛けられる数は $z_1=1+i$ です。複素平面上では $\mathrm{A}(1,1)$ です。

これに $z_2=i$ を掛けることを考えます。$z_2$ は $x$ 軸に対して $90^{\circ}$ の位置にあります。複素平面上では $\mathrm{B}(0,1)$ です。

$i$ を掛けることで $90^{\circ}$ 回転であることを理解したいわけですが、ここでは先に実際に計算にて打点してみます。
$$(1 + i)\times i = i + i^2 = i – 1 = -1 + i$$
なので、$\mathrm{A}^{\prime}(-1,1)$ です。

最後に、本当に回転になっているのか、確かめます。$\mathrm{A}$ を $90^{\prime}$ 回転させると、確かに $\mathrm{A}^{\prime}$ になりました。

一般的な例
今度は、$z_1=\sqrt{3}+i$ に、$z_2=1+\sqrt{3}i$ を掛ける演算を考えます。
$$(\sqrt{3}+i)(1+\sqrt{3}i)=\cancel{\sqrt{3}}+3i+i-\cancel{\sqrt{3}}=4i$$
となります。これを複素平面で表現すると↓のようになります。
ステップ・バイ・ステップで確認します。
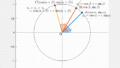
掛けられる数は $z_1=\sqrt{3}+i$ です。複素平面上では $\mathrm{A}(\sqrt{3},1)$ です。

これに $z_2=1+\sqrt{3}i$ を掛けることを考えます。$z_2$ は $x$ 軸に対して $60^{\circ}$ の位置にあります。複素平面上では $\mathrm{B}(1,\sqrt{3})$ です。

$z_2$ を掛けることで $60^{\circ}$ 回転であることを理解したいわけですが、ここでは先に実際に計算にて打点してみます。
$$(\sqrt{3} + i)\times(1+\sqrt{3}i)=\cancel{\sqrt{3}}+3i+i-\cancel{\sqrt{3}}=4i$$
なので、$\mathrm{A}^{\prime}(0,4)$ です。

最後に、本当に回転になっているのか、確かめます。$\mathrm{A}$ を $60^{\prime}$ 回転させると、$\mathrm{A}^{\prime}$ の角度にはなりましたが、長さが異なります。

長さを $2$ 倍すれば、$\mathrm{A}^{\prime}$ に一致します。この $2$ 倍という数は、掛ける数 $z_2$ の大きさ(すなわち、$\mathrm{OB}$ の長さ)です。

このように複素数の乗算は、複素平面上では回転と拡大を意味します。
これを応用すれば三角関数の加法定理も余裕で導ける
三角関数の加法定理は次のような公式です。
$\sin(\alpha+\beta) = \sin\alpha\cos\beta+\cos\alpha\sin\beta$
$\cos(\alpha+\beta) = \cos\alpha\cos\beta-\sin\alpha\sin\beta$
これも、複素数の演算を使えばたちどころに証明できてしまいます。この証明の記事は独立させました。
除法:逆回転と縮小
除法は、乗法の逆操作です。乗法のときの例を逆にして考えてみましょう。乗法では、$z_1=\sqrt{3}+i$, $z_2=1+\sqrt{3}i$ のとき、$z_3=z_1\times z_2=4i$ でした。ここから、$\displaystyle\frac{z_3}{z_2}$ を考えてみます。
\begin{eqnarray}
\frac{z_3}{z_2} &=& \frac{4i}{1+\sqrt{3}i}=\frac{4i(1-\sqrt{3}i)}{(1+\sqrt{3}i)(1-\sqrt{3}i)}\\
&=& \frac{4i+4\sqrt{3}}{1+3}=i+\sqrt{3}\\
&=& \sqrt{3}+i
\end{eqnarray}
となり、当たり前ですが、$z_1$ になりました。つまり、複素平面上では、$z_3$ が $z_2$ の角度である $60^{\circ}$ だけ逆回転し、さらに長さも $z_2$ の長さである $2$ だけ縮小(除算)されたのです。
まとめ
複素数の演算は、単なる数の操作ではなく、複素数平面上の座標変換として理解できます。
✅ 加減 → ベクトルの和と差
✅ 乗算 → 順回転+拡大
✅ 除算 → 逆回転+縮小
この視点を持つことで、数学の世界がより直感的に感じられるはずです。ぜひ、実際に複素数をプロットして動かしてみてください!


コメント