複素数は、計算だけでなく「複素数平面でのイメージ」を活用することで一気に理解が深まります。本記事では、絶対値・共役・四則演算の性質、そして実数・純虚数となる条件を、図や動画を交えながら直感的に整理します。複素数の基本性質を“当たり前”に使えるようになりましょう。
絶対値
$$|z|^2=z\,\overline{z}$$
式で理解
複素数を
$$z = a + b\,i$$
と置くと、
\begin{eqnarray} z\,\overline{z} &=& (a+b\,i)(a-b\,i) = a^2 + b^2 \\ &=& |z|^2 \end{eqnarray}
イメージで理解
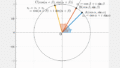
図形的には、次のようなイメージです。
$z$ (青) と $\overline{z}$ (赤) は、複素数平面上で $x$ 軸に対して対称 な位置にあります。

両者を掛けるということは、まず角度を打ち消し合い、

さらに大きさは積になります。

結果として得られる複素数 (黄色) は実部のみを持ち、すなわち 大きさの2乗という実数になります。
複素数の演算が座標変換として理解できることについては、こちらの記事で詳しく扱っています。
だから何?(使いどころ)
「$|z|^2 = z\,\overline{z}$ は分かったけれど、どこで役に立つの?」という疑問が出てくるかもしれません。
例えば、問題でよく出てくる条件 $|z| = 1$。これを見たらすぐに
$$z = \frac{1}{\overline{z}}$$
が使えるかもしれない、と考えましょう。これがこの性質の代表的な使いどころです。
例題
$|z|=1$ のとき、$z+\displaystyle\frac{1}{z}$ は実数であることを示せ。
この例題は、別の性質も使うため、解説は後ろの章にまとめています。
引っかかりやすい罠
$|z|^2 = z\,\overline{z}$ を理解していても、計算の途中で忘れてしまうケースがあります。典型的な罠を見ておきましょう。
$\alpha$, $\beta$ を複素数とするとき、
$$|\alpha+\beta|^2+|\alpha-\beta|^2=2(|\alpha|^2+|\beta|^2)$$
を示せ。
左辺を安易に展開してしまうと罠にハマります。
$$|\alpha+\beta|^2 = |\alpha|^2 + 2\alpha\beta + |\beta|^2$$
これは誤りで、正しくは
$$|\alpha+\beta|^2 = (\alpha+\beta)\overline{(\alpha+\beta)}$$
です。この続きの展開は後ろの章で扱います。
四則演算の性質
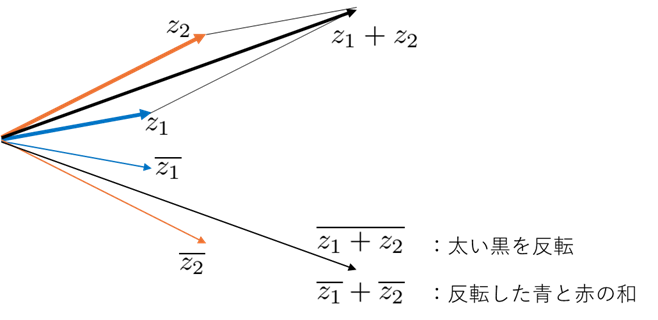
ここでは、複素数の四則演算に関する基本的な性質をまとめます。図形的なイメージを思い浮かべながら確認してみてください。和だけ図で示します。
和と差
$\overline{z_1+ z_2}=\overline{z_1}+\overline{z_2}$
$\overline{z_1- z_2}=\overline{z_1}-\overline{z_2}$
積
$$\overline{z_1\,z_2}=\overline{z_1}\cdot\overline{z_2}$$
商
$$\overline{\left(\frac{z_1}{z_2}\right)}=\frac{\overline{z_1}}{\overline{z_2}}$$
実数・純虚数となる条件
実数となる条件
$$\overline{z}=z$$
イメージで理解
複素数平面で「実数」とは、
実軸上にある点
のことです。共役 $\overline{z}$ は実軸に対して対称なので、$z$ が実軸上ならその共役 $\overline{z}$ も実軸上 にあります。したがって両者は一致します。
式で理解
$z$ が実数なら $z=a+0i$ と書け、共役は
$$\overline{z}=a-0i$$
となり、$z=\overline{z}$ が成り立ちます。
純虚数となる条件
$$\overline{z}=-z$$
イメージで理解
純虚数とは、複素数平面で
虚軸上にある点
のことです。共役 $\overline{z}$ は実軸に対して対称なので、$z$ が虚軸上ならその共役 $\overline{z}$ も虚軸上ですが反対側の $-z$ に来ます。
式で理解
$z=0+bi$ と書けるので、共役は
$$\overline{z}=0-bi$$
となり、確かに $\overline{z}=-z$ です。
垂直に交わる条件
$\displaystyle\frac{\alpha}{\beta}$ が純虚数
複素数平面上の点 $\mathrm{A}(\alpha)$, $\mathrm{B}(\beta)$ に対して
$$\mathrm{OA}\perp\mathrm{OB}$$
となる必要十分条件は、
$\displaystyle\frac{\alpha}{\beta}$ が純虚数
となること。
ここでは厳密な証明よりも、”イメージとしてどう見えるか” を大切にします。
複素数の割り算は、下記記事で扱ったように、
角度の引き算(逆回転)を意味します。つまり、両者のなす角を求めているわけです。
その角度が $90^\circ$ であれば、結果は純虚数になります。
具体例で確かめる
$\alpha=2+i$、$\beta=-2+4i$ のとき、両者は垂直です。割り算によって逆回転され、その結果が虚軸に一致することで、なす角が $90^\circ$ であったと分かります。
実際に計算すると、
\begin{eqnarray}
\frac{\alpha}{\beta} &=& \frac{-2+4i}{2+i} = \frac{-2+4i}{2+i}\frac{2-i}{2-i}\\
&=& \frac{-4+2i+8i+4}{5} \\
&=& 2i
\end{eqnarray}
結果が 純虚数になっているので、$\mathrm{OA}$ と $\mathrm{OB}$ が垂直であることが分かります。
別の表現
割り算の結果を $\omega=\displaystyle\frac{\alpha}{\beta}$ と置くと、垂直である条件は次のようにも書けます。
$$\overline{\omega}=-\omega$$
もしくは
$$\omega+\overline{\omega}=0$$
つい先ほどの例だと $\omega=2i$ ですが、確かに成り立っています。
この話題は 2025 年度の共通テストでも扱われました。詳しくは以下の記事で解説しています。
例題
$|z|=1$ のとき、$z+\displaystyle\frac{1}{z}$ は実数
$|z|=1$ のとき、$z+\displaystyle\frac{1}{z}$ は実数であることを示せ。
実数である条件は こちら $(\overline{z}=z)$。
$|z|=1$ を見たら 絶対値の性質 $\left(z=\displaystyle\frac{1}{\overline{z}}\right)$。
あとは、四則演算の性質 $(\overline{z_1+z_2}=\overline{z_1}+\overline{z_2})$ です。
解答
示すべきことは
$$\overline{\left(z+\frac{1}{z}\right)} = z+\frac{1}{z}$$
です。
\begin{eqnarray} \overline{\left(z+\frac{1}{z}\right)} &=& \overline{z} + \frac{1}{\overline{z}} \\ &=& \frac{1}{z} + z \qquad (\because |z|^2 = z\overline{z} = 1) \end{eqnarray}
よって実数です。
別解(強引に解く方法)
$|z|=1$ なら、$z=\cos\theta+i\sin\theta$ と置けます。
\begin{eqnarray} \frac{1}{\overline{z}} &=& \frac{1}{\cos\theta – i\sin\theta} \\ &=& \frac{\cos\theta+i\sin\theta}{\cos\theta+i\sin\theta} \\ &=& \cos\theta+i\sin\theta \end{eqnarray}
したがって、
\begin{eqnarray} \overline{\left(z+\frac{1}{z}\right)} &=& \overline{z} + \frac{1}{\overline{z}} \\ &=& (\cos\theta – i\sin\theta) + (\cos\theta + i\sin\theta) \\ &=& 2\cos\theta \end{eqnarray}
よって実数です。
複素数の逆数という発想
より骨太に理解するため、複素数の逆数をテーマにした下記の記事も参考にしてください。
$|\alpha+\beta|^2+|\alpha-\beta|^2=2(|\alpha|^2+|\beta|^2)$
$\alpha$, $\beta$ を複素数とするとき、
$$|\alpha+\beta|^2+|\alpha-\beta|^2=2(|\alpha|^2+|\beta|^2)$$
を示せ。
安易に展開せず、絶対値の性質 $(|z|^2=z\,\overline{z})$ を使って展開します。
解答
\begin{eqnarray} |\alpha+\beta|^2 &=& (\alpha+\beta)\overline{(\alpha+\beta)} \\ &=& (\alpha+\beta)(\overline{\alpha}+\overline{\beta}) \\ &=& \alpha\overline{\alpha} + \alpha\overline{\beta} + \beta\overline{\alpha} + \beta\overline{\beta} \end{eqnarray}
同様に、
\begin{eqnarray} |\alpha-\beta|^2 &=& (\alpha-\beta)\overline{(\alpha-\beta)} \\ &=& (\alpha-\beta)(\overline{\alpha}-\overline{\beta}) \\ &=& \alpha\overline{\alpha} – \alpha\overline{\beta} – \beta\overline{\alpha} + \beta\overline{\beta} \end{eqnarray}
よって、
\begin{eqnarray} |\alpha+\beta|^2 + |\alpha-\beta|^2 &=& 2(\alpha\overline{\alpha} + \beta\overline{\beta}) \\ &=& 2(|\alpha|^2 + |\beta|^2) \end{eqnarray}
図形的意味
この式を図形的に解釈すると次のようになります。
平行四辺形の
対角線の長さの二乗の和 = 各辺の長さの和の2倍
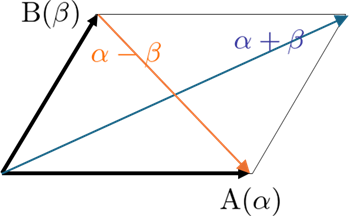
式と平行四辺形を見比べると、
- $|\alpha+\beta|$ : 青の対角線の長さ
- $|\alpha-\beta|$ : 赤の対角線の長さ
- $|\alpha|$, $|\beta|$ : 黒の辺の長さ
だからです。これらの間にこのような関係が成り立っていることが、複素数で証明できたことになります。
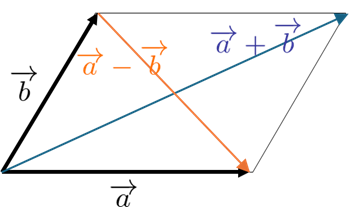
ベクトルでの証明
同じことをベクトルで証明することもできます。
$\overrightarrow{a}$, $\overrightarrow{b}$ に対し、
$$|\overrightarrow{a}+\overrightarrow{b}|^2+|\overrightarrow{a}-\overrightarrow{b}|^2=2(|\overrightarrow{a}|^2+|\overrightarrow{b}|^2)$$
を示せ。
\begin{eqnarray}
|\overrightarrow{a}+\overrightarrow{b}|^2+|\overrightarrow{a}-\overrightarrow{b}|^2 &=& |\overrightarrow{a}|^2+2\;\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2\\
&+&|\overrightarrow{a}|^2-2\;\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2\\
&=& 2(|\overrightarrow{a}|^2+|\overrightarrow{b}|^2)
\end{eqnarray}
まとめ
複素数の基本性質(絶対値・共役・四則演算)は、複素数平面で考えると驚くほど自然に理解できます。これらを“当たり前”に使えるようになると、計算問題や証明問題が一気に楽になります。
より図形的な理解を深めたい方は次の記事で扱う「複素数の軌跡」に進むと世界が深まります。






コメント