前稿と同じ図形を別の角度から問題にしました。前稿との違いを踏まえて問題を解いてみてください。これまでの発想が点と点でバラバラであったところ、それが線で結ばれる感覚が得られると思います。
円周角の定理を用いて二等辺三角形から相似を作る
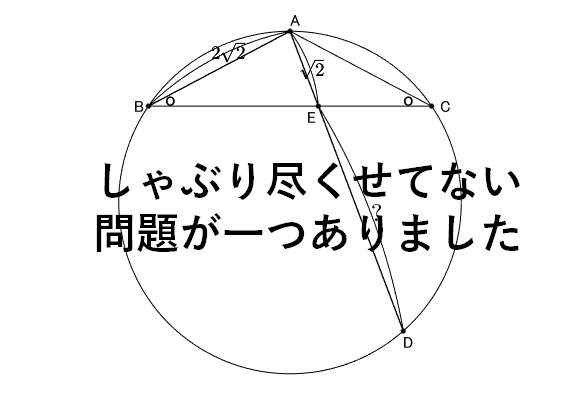
問題
$?$ を求めよ。

この図形は前稿で見た図形↓を $180^\circ$ 回転させてモノであることに気づきますでしょうか?下記の記事を読んでいない人は、読む前にまずは解けるかやってみてください。その後、読んでくださいね!
解答は一気にこのアニメーションで確認します。
円周角の定理で角度を移動する
円周角の定理より
$$\angle\mathrm{ACB}=\angle\mathrm{ADB}$$
です。


相似を発見する
$$\angle\mathrm{ADB}=\angle\mathrm{ABE}$$
で、角$\angle\mathrm{A}$ 共通より、
$$\triangle\mathrm{ADB}\unicode[sans-serif]{x223D}\triangle\mathrm{ABE}$$
です。下記の右図は左図を反転させ、相似をイメージしやすくしたものです。


比例式を立てる
$$\triangle\mathrm{ADB}\unicode[sans-serif]{x223D}\triangle\mathrm{ABE}$$
から、
\begin{eqnarray}
\mathrm{AD}:\mathrm{AB} &=& \mathrm{AB}:\mathrm{AE}\\
\mathrm{AD}\times\mathrm{AE} &=& (\mathrm{AB})^2\\
\mathrm{AD}\times \sqrt{2} &=& (2\sqrt{2})^2\\
\therefore\;\mathrm{AD} &=& 4\sqrt{2}\\
\therefore\;\mathrm{ED} &=& 3\sqrt{2}\;\;(\because\,\mathrm{AE}=\sqrt{2})
\end{eqnarray}
答え
よって答えは
$$3\sqrt{2}$$
まとめ
前稿の続きで、同じ問題をさらに一つ別の角度から眺めました。前稿との違いは、
- 前稿は、角の二等分線を出発点として、円周角の定理で角度を移動することで相似を作った
- 本稿は、二等辺三角形を出発点として、円周角の定理で角度を移動することで相似を作った
です。
その完成形の図形はどちらも同じなので、どこを出発点とするかだけの違いです。このように出題の切り口が変わっても対応できるよう、一つの問題をしゃぶり尽くす勉強をしていってください。



コメント