「積分は微分の逆」と言われますが、なぜ逆になるのかを “イメージで理解できている人” は意外と少ないものです。
微分積分学の基本定理は高校数学の中でも特に抽象的で、「結局どういう意味なの?」と感じる人が多いテーマです。この記事では、微分積分学の基本定理が “直感的に腑に落ちる” ように、図とイメージを使って徹底的に解説します。
- 積分は『微小な量の足し合わせ』であることの復習
- なぜ積分は微分の逆になるのか?
- グラフで見ると何が起きているのか?
これらを順番に見ていくことで、公式の丸暗記ではなく “本質的な理解“ができるようになります。
積分は 『微小な量の足し合わせ』
まず、積分が微分の逆演算かどうかは別にして、積分は文字通り “微小な量の足し合わせ” を意味する演算です。この発想は太古の昔からありましたが、これが微分の逆演算であると気づいたのはニュートンやライプニッツで、比較的最近のことです。
記号としての意味だけをとらえれば、
$$\int_a^bf^\prime(x)\,dx$$
は、『$f^\prime(x)\,dx$ を、$x=a$ から $x=b$ まで足し合わせる』という意味です。
この意味をより深く理解したい方は下記の記事も参考にしてください(ただし、「積分=微分の逆演算」を既知として書いています)。
なぜ積分は微分の逆になるのか?
微分は接線の傾き
まずは微分の復習から。微分はご存じの通り、接線の傾きを表します。
ここで、$f(x)$ の微分を $f^\prime(x)$ と書くことにします。ただし今の時点では、『 $f^\prime(x)$ を積分すると $f(x)$ に戻る』という事実はまだ知りません。これから理解していく段階です。
$ dy=f^\prime(x)\,dx$ の意味
$f(x)$ を微分すると $f^\prime(x)$ なので、
$$\frac{dy}{dx}=f^\prime(x)$$
これを分数のように扱って分母の $dx$ を払うと、
$$dy=f^\prime(x)\,dx$$
となります。これは何を意味しているのでしょうか?
$f^\prime(x)\,dx$ は、グラフ $y=f(x)$ において微小距離 $dx$ だけ進んだ時の $y$ の変化量を表す
図で表すと下記のようになります。
(微小区間 $dx$ に対して、接線の傾き $f^\prime(x)$ に沿って $y$ がどれだけ増えているかを示しています。)

$ f^\prime(x)\,dx$ を足し合わせるとどうなるか?
微小変化量 $f^\prime(x)\,dx$ を $x=a$ から $x=b$ まで足し合わせると、
$$\int_a^b f^\prime(x)\,dx$$
になります。ではこれが本当に $f(x)$ に戻るのでしょうか?
具体例:3分割で考える
例として $x=1$ から $x=2$ までを3分割して考えます。
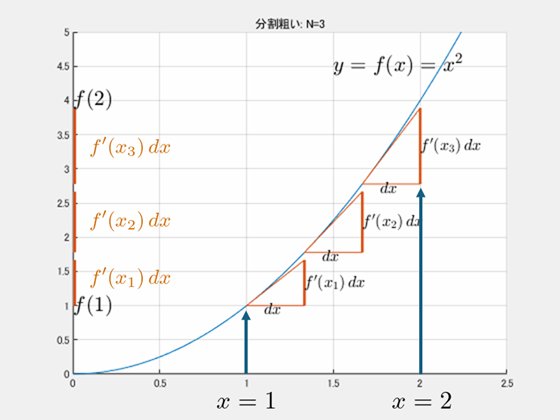
3つの和は、
$$f^\prime(x_1)\,dx+f^\prime(x_2)\,dx+f^\prime(x_3)\,dx$$
ですが、これは
$$f(2)-f(1)$$
に近づいているように見えませんか? これは、「接線の傾き $\times$ 幅($dx$)」が、その区間での $y$ の増加量を近似しているためです。
記号で書くと、
$$\sum_{k=1}^3 f^\prime(x_k)\,dx\approx f(2)-f(1)$$
です。
グラフで見ると何が起きているのか?
アニメーションで確認
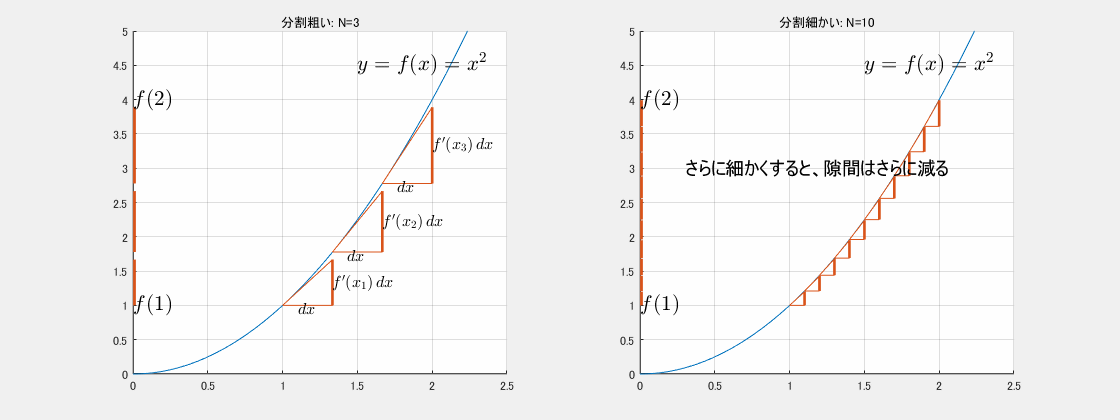
3分割ではまだ粗いですが、分割を細かくしていくと、和はどんどん
$$f(2)-f(1)$$
に近づいていきます。
100分割まで細かくすれば、もはや隙間はほとんどありません。実際には $dx$ はもっと細かく、和の記号 $\sum$ は
$$\int$$
と書きます。したがって、
$$\int_1^2 f^\prime(x)\,dx=f(2)-f(1)$$
となり、積分が微分の逆演算であることが示されました。
まとめ
- $f^\prime(x)\,dx$ は、微小区間 $dx$ における $y$ の変化量 $dy$
- その総和である $\int_a^bf^\prime(x)\,dx$ は、区間全体の変化量
- よって、
$$\int_a^b f^\prime(x)\,dx=f(b)-f(a)$$
となる。
積分は “微小な量の足し合わせ”、微分は “変化の瞬間”。この2つがつながるのが、微分積分学の基本定理です。
関連記事:積分とは何か?





コメント