通過領域や軌跡の問題は「順像法」と「逆像法」のどちらで解くかで見通しが大きく変わります。
この記事では、典型例5つを両方の方法で解き比べることで、2つの解法の違いと使い分けを体系的に理解できます。
多くの問題はこれらの型のどれかに入ると思いますので、問題集などで問題を解いた際にはここに戻って再確認してください。
二次関数 $y=x^2-2x+3$ の通過領域(順像法と逆像法)
$x$ が実数全体を動くとき、$y=x^2-2x+3$ の 取りうる範囲を求めよ。
【この例題の狙い】順像法と逆像法の違いが最もシンプルに表れる基本パターン。
順像法
解
$$\begin{eqnarray}
y&=&(x-1)^2+2\\
&\ge& 2
\end{eqnarray}$$
イメージ
最も簡単な順像法の例です。これまであえて順像法と意識はしていなかったと思いますが、この際に次の逆像法との違いを意識できるとその後の理解も容易になりますので、最初に持ってきました。
【動画の見どころ】この後に逆像法の動画も出てきますが、その際には
- 順像法では $x$ を動かす
- 逆像法では $y$ を動かす
この違いを意識して見ると理解が深まります。
逆像法
この問題は順像法で解けば十分ですが、逆像法のイメージを持つためにあえて逆像法で解きます。
解
与式を $x$ で整理して
$$x^2-2x+3-y=0$$
これを $x$ に関する二次方程式とみてその判別式を $D$ と置くと、$x$ が実数解を持てばよいので、
$$\begin{eqnarray}
\frac{D}{4}&=&1^2-1\cdot(3-y)\\
&=& y-2\\
&\ge& 0
\end{eqnarray}$$
$$\therefore\; y\ge 2$$
イメージ
求めたい $y$ の方をスイープします。そして、その $y$ を与える $x$ が存在するかどうかを記録していくイメージです。
直線群 $y=2tx-t^2$ の通過領域($t$ が実数全体を動く場合)
$t$ が実数全体を動くとき、直線 $y=2tx-t^2$ が通過する領域を図示せよ。
詳しくは【通過領域:順像法】【通過領域:逆像法】で述べていますので、ここでは解答をシンプルに載せるだけにします。
順像法
解
直線の式を $t$ で整理して
$$\begin{eqnarray}
y &=& -t^2+2tx\\
&=& -(t-x)^2+x^2\\
&\le& x^2
\end{eqnarray}$$
$$\therefore\; y\le x^2$$
逆像法
解
直線の式を $t$ で整理して
$$t^2-2xt+y=0$$
これを $t$ に関する二次方程式とみてその判別式を $D$ と置くと、$t$ が実数解を持てばよいので、
$$\begin{eqnarray}
\frac{D}{4} &=& x^2-y\\
&\ge&0
\end{eqnarray}$$
$$\therefore\; y\le x^2$$
二次曲線 $x^2+xy+y^2=1$ の通過領域($y$ の範囲)
$x$, $y$ が $x^2+xy+y^2=1$ を満たして動くとき、$y$ の範囲を求めよ。
順像法
解
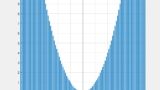
$x^2+xy+y^2=1$ のグラフは下記となる。

$$\therefore\; -\frac{2}{3}\sqrt{3}\le y\le \frac{2}{3}\sqrt{3}$$
イメージ
順像法は基本的にはグラフの最大最小問題です。しかしこのグラフを書くのは容易ではないので、試験の解答としては次の逆像法の方がよいです。自習のときにはこのようにグラフを書いて確かめてみましょう。グラフの描画はWolfram Alphaを利用できます。
逆像法
解
与式を $x$ で整理して、
$$x^2+yx+y^2-1=0$$
これを $x$ に関する二次方程式とみてその判別式を $D$ と置くと、$x$ が実数解を持てばよいので、
$$\begin{eqnarray}
D&=&y^2-4\cdot (y^2-1)\\
&=& -3y^2+4\\
&\ge& 0
\end{eqnarray}$$
より、$y^2\le \displaystyle\frac{4}{3}$
$$\therefore\; -\frac{2}{3}\sqrt{3}\le y\le \frac{2}{3}\sqrt{3}$$
イメージ
求めたい $y$ の方をスイープします。そして、その $y$ を与える $x$ が存在するかどうかを記録していきます。
円 $x^2+y^2=1$ 上での $x+y$ の範囲(順像法と逆像法)
$x$, $y$ が $x^2+y^2=1$ を満たして動くとき、$x+y$ の取りうる範囲を求めよ。
順像法
解
$x^2+y^2=1$ のグラフは $xyz$ 空間上で円柱、$z=x+y$ のグラフは平面であり、下図のようになる。

両式を同時に満たす $x,y,z$ は図の交線であり、求める値は $z$ の範囲なので、
$$-\sqrt{2}\le x+y \le \sqrt{2}$$
イメージ
このグラフも書くのは容易ではないので、次の逆像法の解法の方がよいです。
逆像法
解1
$k=x+y$ と置き、$y=k-x$ として $x^2+y^2=1$ に代入して $x$ について整理すると、
$$x^2+(k-x)^2=1$$
$$2x^2-2kx+k^2-1=0$$
これを $x$ に関する二次方程式とみてその判別式を $D$ と置くと、$x$ が実数解を持てばよいので、
$$\begin{eqnarray}
D&=&k^2-2\cdot (k^2-1)\\
&=& -k^2+2\\
&\ge& 0
\end{eqnarray}$$
より、$k^2\le 2$
$$\therefore\; -\sqrt{2}\le y\le \sqrt{2}$$
解2
$x^2+y^2=1$ と $k=x+y$ が $x,y$ について解を持つためには、原点と直線 $k=x+y$ との 距離を $d$ と置くと、
$$d\le 1$$
ならよい。直線は、$x+y-k=0$ であるから、
$$\begin{eqnarray}
d&=&\frac{|1\times 0+1\times 0-k|}{\sqrt{1^2+1^2}}\\
&=& \frac{|k|}{\sqrt{2}}\\
&\le& 1
\end{eqnarray}$$
より、$|k|\le\sqrt{2}$
$$\therefore\; -\sqrt{2}\le k\le\sqrt{2}$$
イメージ
求めたい $k$ をスイープします。交点が存在する(すなわち、実数解 $x$ が存在する) $k$ の範囲を求めます。実数解 $x$ が存在する条件を、[解1]では判別式で、[解2]では距離という図形的な考察で求めています。
2直線 $mx-y=0$, $x+mx=1$ の交点の軌跡($m$ が動く場合)
2直線 $mx-y=0$, $x+my=1$ がある。$m$ が実数全体を動くとき、2直線の交点P $(x,y)$ の軌跡を求めよ。
順像法
解
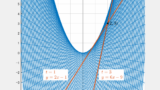
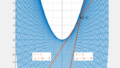
$mx-y=0$, $x+mx=1$ のグラフは下図となる。
右側の図は、左側の図を真上から($+m$ の方向から)見たものである。

$$\therefore\;\left(x-\frac{1}{2}\right)^2+y^2=\frac{1}{4}$$
ただし、$(0,0)$ は除く
イメージ
これは、2次元空間における交点の軌跡問題を3次元空間に一つ次元を上げることによって直接に交点を求める問題としてとらえたものです。しかしこの解は試験では使えません。なぜなら、まず、このようなグラフをCG無しで書くことは無理だからです。また、仮に書けたとしてもその交線がこの解にあるような方程式になることを証明していないからです。これは、逆像法をより意識できるよう、あえて順像法を持ってきた狙いであり、また交点の軌跡問題をより直接的に理解する狙いです。
交点の軌跡問題について詳しくは【軌跡はパラメータを消去】なぜこれで軌跡が求まるのかを完全理解をどうぞ。
逆像法
解
(i) $x\ne 0$ のとき、$mx-y=0$ より、$m=\displaystyle\frac{y}{x}$
これを $x+mx=1$ に代入して整理すると、
$\left(x-\displaystyle\frac{1}{2}\right)^2+y^2=\displaystyle\frac{1}{4},\quad$ただし、$(0,0)$ は除く
(ii) $x=0$ のとき、$mx-y=0$ より $y=0$。
しかしこれは $x+mx=1$ を満たさない。
(i)(ii) より求める軌跡は、
$\left(x-\displaystyle\frac{1}{2}\right)^2+y^2=\displaystyle\frac{1}{4},\quad$ただし、$(0,0)$ は除く
イメージ
$m$ を消去していますが、これこそが図の右側の気持ちです。つまり、真上から見ることで $m$ の情報を消去しており、つまり、$m$ が実数全体を動いた時の全てを圧縮して見ています。
まとめ
【順像法と逆像法の使い分けまとめ】
| 解法 | 強み | 弱み | 向いている課題 |
|---|---|---|---|
| 順像法 | 直感的・グラフで理解しやすい | グラフが描けないと詰む | 基本問題 |
| 逆像法 | 計算で確実に求まる | イメージが沸きにくい | 試験問題・複雑な式 |
それぞれを単独で解説してる記事や参考書はよくありますが、両方を比較しながら解説している記事はここオリジナルではないかと思います。両方を比較することでそれぞれの長所と短所がよくわかり、それぞれの理解がより深まると思います。
順像法と逆像法をさらに深く理解したい方は、以下の解説記事が役に立ちます。
どちらもこの記事とセットで読むと理解が一気に深まります。



コメント